Quarta dimensão

O conceito de uma quarta dimensão[nota 1] é algo frequentemente descrito considerando-se as suas implicações físicas; isto é, sabemos que em três dimensões temos as dimensões de comprimento (ou profundidade), largura e altura. A quarta dimensão (espacial) é ortogonal às outras três dimensões espaciais. As direções principais nas três dimensões conhecidas são chamadas de em cima/baixo (altitude), norte/sul (latitude) e leste/oeste (longitude). Quando falamos da quarta dimensão, termos adicionais são necessários. Entre aqueles comumente empregados, incluem-se ana/kata (algumas vezes chamados de spissitude/spassitude), vinn/vout (usados pelo escritor Rudy Rucker) e upsilon/delta.[vago]
Para ser mais preciso, a quarta dimensão deveria ser identificada com o tempo (ou dimensão temporal). Todavia, entre as décadas de 1870 e 1920 na Grã-Bretanha e nos Estados Unidos, a expressão caiu no gosto popular com o significado de "quarta dimensão espacial" (ou seja, seria na verdade uma "quinta dimensão") e daí disseminou-se por todos os campos das artes e ciências, tornando-se "uma metáfora para o estranho e o misterioso" (Kaku, 2000, p. 41). Portanto, este artigo discute as implicações da quarta dimensão como mais uma dimensão espacial, e não no sentido que lhe é dado, por exemplo, para explicar as teorias sobre o espaço-tempo de Einstein.
Conceitos
A quarta dimensão e a ortogonalidade
Um ângulo reto pode ser definido como um quarto de volta. A geometria cartesiana escolhe arbitrariamente direções ortogonais através do espaço que se constituem em ângulos retos entre si. Três dimensões ortogonais do espaço são conhecidas como comprimento, largura e altura. Portanto, a quarta dimensão é a direção no espaço que está em ângulo reto com estas três dimensões observáveis.
Espaços vetoriais

Um espaço vetorial é um conjunto de vetores, que podemos imaginar como flechas presas num determinado lugar do espaço (chamado de origem) e que apontam para outros lugares.
Um ponto é um objeto com zero dimensão. Não tem extensão no espaço, nem propriedades. Se pensarmos neste ponto como um vetor geométrico, como uma flecha, ele não teria comprimento. Este vetor é chamado de vetor zero e, por si mesmo, constitui-se no vetor espacial mais simples.
Uma reta é um objeto unidimensional. Se puxarmos um vetor não-zero em alguma direção, ele terá um comprimento definido. Este vetor tem a cabeça em algum ponto no espaço e a cauda na origem. Se pensarmos em esticar este vetor duas, três vezes e assim por diante, de modo que ele assuma todos os comprimentos possíveis (mesmo zero, para obter o vetor zero), teremos uma linha única com uma dimensão de comprimento. Todos os vetores que descrevem pontos nesta linha são ditos como sendo paralelos um ao outro. E mesmo que qualquer linha que possamos desenhar tenha alguma espessura mínima (para que possamos vê-la), esta linha idealizada não a possui.
Um plano é um objeto bidimensional. Ele tem comprimento e largura mas não espessura — algo como uma folha de papel (mas mesmo o papel tem alguma espessura). Pensar num plano em termo de vetores é um pouco mais complicado. Se imaginarmos pegar um vetor e movê-lo de modo que sua cauda tocasse a cabeça do antecedente e formasse um vetor com sua cauda na origem e a cabeça na cabeça do segundo vetor reposicionado, teremos um modo razoável de falar sobre soma de vetores. Se tivermos dois vetores que não sejam paralelos, poderemos falar de todos os pontos que podemos atingir esticando um ou nenhum dos vetores e, somando estes vetores em conjunto, seus pontos formarão um plano.
O espaço, tal como o percebemos, é tridimensional. Imaginemos colocar uma linha num plano. Ambos estão juntados como num sanduíche. Para ir para um determinado ponto no espaço, podemos imaginar viajar ao longo da linha e então se mover através do plano até o ponto. Temos então três vetores para considerar, um para viajar até certa distância ao longo da linha e dois para atingir um determinado ponto no espaço.
A quarta dimensão, então, sendo assim, pode ser descrita como a junção de vários espaços tridimensionais numa linha. Para atingir um ponto determinado no espaço quadridimensional, viaja-se ao longo de espaços tridimensionais e também através da quarta dimensão. A quantidade total de vetores envolvidos é quatro.
Analogia dimensional
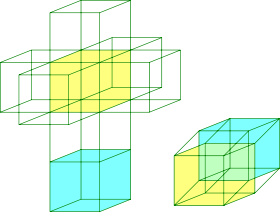
Para fazer o salto de três para quatro dimensões, emprega-se comumente um truque denominado "analogia dimensional". Analogia dimensional é estudar como (n – 1) dimensões se relacionam com "n" dimensões e então deduzir como “n” dimensões se relacionariam com (n + 1) dimensões.
Por exemplo, no livro Flatland ("Planolândia - um romance de muitas dimensões"), Edwin Abbott escreve sobre um certo Sr. Quadrado que vive num mundo bidimensional, como a superfície de uma folha de papel. Um ser tridimensional (uma esfera) surge em seu mundo e parece (do ponto de vista do "chatalandês") ter poderes quase divinos: é capaz de tirar objetos de dentro de um cofre sem abri-lo (ou seja, movendo-o através da terceira dimensão), ver através das paredes (bidimensionais) e ficar completamente invisível apenas movendo-se umas poucas polegadas na terceira dimensão. Ao aplicar a analogia dimensional, pode-se deduzir que um ente quadridimensional seria capaz de feitos similares da nossa perspectiva tridimensional. Rudy Rucker demonstra isto em seu romance "Spaceland", na qual o protagonista encontra seres quadridimensionais que demonstram tais poderes.
Uma aplicação útil da analogia dimensional em visualizar a quarta dimensão está na projeção. Uma projeção é um modo de representar um objeto n-dimensional em n − 1 dimensões. Por exemplo, telas de computador são bidimensionais, e todas as fotografias de pessoas, coisas e lugares tridimensionais são representadas em duas dimensões, removendo-se a informação sobre a terceira dimensão. Neste caso, a profundidade é removida e substituída por informação indireta. A retina do olho é uma matriz de receptores bidimensional, mas ela permite que o cérebro perceba a natureza de objetos tridimensionais usando informações indiretas (tais como sombreado, perspectiva, visão binocular, etc.) para dar profundidade tridimensional a imagens bidimensionais.
De forma similar, objetos na quarta dimensão podem ser matematicamente projetados nas 3 dimensões familiares, onde elas podem ser então mais convenientemente examinadas. Neste caso, a "retina" do olho quadridimensional é uma matriz de receptores tridimensionais. Um ser hipotético com tal visão poderia perceber a natureza de objetos quadridimensionais usando informações indiretas contidas na imagem que recebe em sua retina. A projeção em quatro dimensões produz efeitos semelhantes às do caso tridimensional, tais como perspectiva. Isto acrescenta profundidade quadridimensional à estas imagens.

A analogia dimensional também ajuda a entender tais projeções. Por exemplo, objetos bidimensionais são delimitados por limites unidimensionais: um quadrado é delimitado por quatro bordas. Objetos tridimensionais são delimitados por superfícies bidimensionais: um cubo é delimitado por 6 quadrados. Aplicando-se analogia dimensional, pode-se deduzir que um cubo quadridimensional, conhecido como tesseract, é delimitado por volumes tridimensionais. E realmente, este é o caso, matematicamente falando: o tesseract é delimitado por 8 cubos. Saber isto é a chave para compreender a interpretação tridimensional de uma projeção do tesseract. Os limites do tesseract projetam-se em "volumes" na imagem, não meramente em superfícies bidimensionais. Isto ajuda a entender características de tais projeções que, de outra forma, seriam muito intrigantes.
Igualmente, o conceito das sombras nos ajuda a entender melhor a teoria das quatro dimensões. Se você lançar uma luz sobre um objeto tridimensional, ele irá projetar uma sombra bidimensional. Logo, a luz que incide sobre um objeto bidimensional projetará uma sombra unidimensional (num mundo bidimensional), e a luz sobre um objeto unidimensional num mundo unidimensional projetará uma sombra zero-dimensional, ou seja, um ponto sem luz. Esta ideia pode ser usada em outra direção; uma luz lançada sobre um objeto quadridimensional projetará uma sombra em três dimensões.
Como exemplo disso, imagine-se que uma luz seja emitida obliquamente através de um cubo de arame, sobre uma superfície plana. A sombra resultante é a de um quadrado dentro de um quadrado com cada um dos lados conectados (veja a figura 4). Similarmente, se um cubo quadridimensional fosse iluminado "obliquamente", sua sombra seria a de um cubo tridimensional dentro de outro cubo tridimensional (veja as figuras 3 e 4).
Seres tridimensionais são capazes unicamente de ver o mundo com seus olhos em duas dimensões; um ser quadridimensional veria o mundo em três. Assim, seria capaz de, por exemplo, ver os seis lados de uma caixa opaca simultaneamente. E não somente isso; simultaneamente, ele seria também capaz de ver o que está dentro da caixa, da mesma forma que em Flatland, onde a Esfera vê objetos no mundo bidimensional e tudo que está dentro deles, ao mesmo tempo. Analogamente, um observador quadridimensional veria todos os pontos em nosso espaço tridimensional simultaneamente, incluindo a estrutura interna de objetos e coisas sólidas, ocultas do nosso ponto-de-vista tridimensional.
Observando a animação acima, quando a movimentação para a troca de posição com o cubo que outrora estava no centro e interior do cubo maior se posiciona exatamente ao centro, podemos contar neste instante 26 dimensões distintas e unidas ao mesmo tempo, que sempre estão se movimentando e trocando de posição.
Os poliedros de Schläfli
Os polígonos são traçados no plano e os poliedros no espaço de dimensão 3. Os objetos análogos em dimensão 4 levam o nome geral de politopos ainda que, bem freqüentemente, se continue a chamá-los simplesmente de poliedros.
Como Platão discutiu poliedros regulares no espaço usual de dimensão 3, Schäfli descreveu poliedros regulares em dimensão 4. Trata-se de uma das mais bonitas contribuições de Schläfli: a descrição precisa de seis poliedros regulares em dimensão 4. Como são em dimensão 4, têm vértices, faces de dimensão 2 e faces de dimensão 3. Eis um quadro que indica os nomes destes poliedros.
| nome | figura |
|---|---|
| sixplexo |  |
| hipercubo | 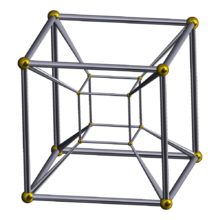 |
| 16 |  |
| 24 |  |
| 120 |  |
| 600 |  |
Quarta dimensão na ficção científica e cultura popular
Cultura popular
- A quarta dimensão tem sido assunto de fascinação popular desde pelo menos 1877, quando ocorreu em Londres o julgamento do médium Henry Slade, que afirmava ter o poder de manipular objetos na quarta dimensão (retirá-los de dentro de cofres fechados, por exemplo).
- A maioria dos simuladores de movimento usa o termo 4-D como propaganda, referindo-se ao movimento dos assentos como "quarta dimensão".
- A quarta dimensão influenciou as criações de Pablo Picasso e Marcel Duchamp, bem como os movimentos cubista e expressionista. A quarta dimensão também foi citada em obras literárias de Oscar Wilde, Fiódor Dostoiévski, Marcel Proust e Joseph Conrad, e está presente em músicas escritas por Alexander Scriabin. Despertou grande atenção de outras personalidades, como William James, Gertrude Stein e até mesmo de Vladimir Lenin.
- Salvador Dali usou o tesseract em sua famosa pintura Corpus Hypercubus, ou Crucifixion que retrata Cristo crucificado numa cruz quadridimensional.
- Alex Garland escreveu um romance intitulado "O tesseracto" (ISBN 85-325-1217-8), onde entrelaça as trajetórias de vida de vários personagens, como se estivesse montando o hipercubo citado no título.
Ficção científica
- Ray Cummings publicou um livro de ficção científica, em 1926, intitulado Into the Fourth Dimension.
- Robert A. Heinlein escreveu um conto de FC considerado clássico e que envolve a quarta dimensão: "...And He Built a Crooked House...".
- Na graphic novel "From Hell" de Alan Moore, o autor utiliza a quarta dimensão como uma referência para a insanidade do personagem Jack, o Estripador.
- "Matadouro Cinco" de Kurt Vonnegut apresenta extraterrestres que se referem à quarta dimensão como sendo o contínuo tempo-espaço que existe junto a Júpiter e às suas luas.
- O "Viajante" em A Máquina do Tempo de H. G. Wells[2] identifica o tempo como a quarta dimensão (o que, num sentido restrito, ele o é), da mesma forma que faz o Doutor no primeiro episódio da série de TV e também o livro "Uma dobra no tempo", de Madeleine L'Engle.
- Em Jimmy Neutron, o personagem-título tem um pequeno cubo (que chama de hipercubo), o qual serve como um portal para a quarta dimensão (ele a usa simplesmente como área de armazenamento).
- Em De volta para o Futuro - Parte III, Doc Brown faz várias referências à quarta dimensão, no sentido em que a máquina do tempo instalada em um carro também atravessa a quarta - "Marty, você não está pensando quadridimensionalmente!" - e assim faz a transição do espaço tridimensional em um período para outro.
- A quarta dimensão é citada no filme Donnie Darko (2001), onde uma anomalia nessa dimensão ocasiona a criação de universos paralelos.
Notas
Ver também
Bibliografia
- KAKU, Michio. Hiperespaço: uma odisséia científica através de universos paralelos, empenamento do tempo e a décima dimensão. Rio de Janeiro: Rocco, 2000. Série Ciência Atual. ISBN 85-325-1046-9.
Referências
- ↑ «Dimensions Capitulo 3/4». www.dimensions-math.org. Consultado em 13 de junho de 2016
- ↑ Einstein e Picasso: mera coincidência?
- ↑ Dicionário Eletrônico Houaiss de Língua Portuguesa 3.0 (2009). Espaço e Dimensão. [S.l.]: Objetiva Ltda
Ligações externas
- (em inglês)-O Reconhecimento da Quarta Dimensão por Charles H. Hinton, inventor do termo tesseract.
- (em inglês)-A Quarta Dimensão Explicada
- (em inglês)-Garrett Jones' tetraspace page
- (em inglês)-Flatland: a Romance of Many Dimensions
- (em inglês)-Visualização 4D
- (em inglês)-TeV scale gravity, mirror universe, and ... dinosaurs Artigo da Acta Physica Polonica B por Z.K. Silagadze.
- (em inglês)-Mushware: Vídeo Games Quadridimensionais