Criptografie

Criptografia reprezintă o ramură a matematicii care se ocupă cu securizarea informației precum și cu autentificarea și restricționarea accesului într-un sistem informatic. În realizarea acestora se utilizează atât metode matematice (profitând, de exemplu, de dificultatea factorizării numerelor foarte mari), cât și metode de criptare cuantică. Termenul criptografie este compus din cuvintele de origine greacă κρυπτός kryptós (ascuns) și γράφειν gráfein (a scrie).
Criptologia este considerată ca fiind cu adevărat o știință de foarte puțin timp. Aceasta cuprinde atât criptografia - scrierea secretizată - cât și criptanaliza. Scrierea secretizată se efectuează cu ajutorul unui cod de semne convenționale.[1] De asemenea, criptologia reprezintă nu numai o artă veche, ci și o știința nouă: veche pentru că Iulius Cezar a utilizat-o deja, dar nouă pentru că a devenit o temă de cercetare academico-științifică abia începând cu anii 1970. Această disciplină este legată de multe altele, de exemplu de teoria numerelor, algebră, teoria complexității, informatică.
Terminologie
Până în vremurile moderne, termenul criptografie se referea aproape exclusiv la criptare, procesul de conversie a informației obișnuite (text în clar) într-un text neinteligibil (text cifrat).[2] Decriptarea este inversul, trecerea de la textul cifrat, neinteligibil, în text clar. Un cifru este o pereche de algoritmi care efectuează atât această criptare cât și decriptarea. Modul de operare detaliat al unui cifru este controlat de algoritm și de o cheie. Această cheie este un parametru secret (în mod ideal, cunoscut doar celor care comunică) pentru contextul unui anume schimb de mesaje. Cheile sunt importante, iar cifrurile fără chei variabile sunt simplu de spart și deci mai puțin utile. De-a lungul istoriei, cifrurile erau adesea folosite direct pentru criptare și decriptare, fără proceduri adiționale, cum ar fi autentificarea sau testele de integritate.
În utilizarea populară, termenul "cod" este adesea folosit cu sensul de orice metodă de criptare sau de ascundere a înțelesului. Totuși, în criptografie, cuvântul cod are un înțeles mai restrâns; acela de înlocuire a unei unități de text clar (un cuvânt sau o frază) cu un cuvânt codat (de exemplu, plăcintă cu mere înlocuiește atac în zori). Codurile nu mai sunt folosite în criptografie, decât uneori pentru anumite lucruri cum ar fi desemnarea unităților (de exemplu, "zborul Bronco" sau Operațiunea Overlord) — întrucât cifrurile alese corect sunt mai practice, mai sigure și în același timp mai bine adaptate calculatoarelor decât cele mai bune coduri.
Istoria criptografiei și criptanalizei

Înainte de epoca modernă, criptografia se ocupa doar cu asigurarea confidențialității mesajelor (criptare) — conversia de mesaje dintr-o formă comprehensibilă într-una incomprehensibilă, și inversul acestui proces, pentru a face mesajul imposibil de înțeles pentru cei care interceptează mesajul și nu au cunoștințe secrete adiționale (anume cheia necesară pentru decriptarea mesajului). În ultimele decenii, domeniul s-a extins dincolo de problemele de confidențialitate și include, printre altele, și tehnici de verificare a integrității mesajului, autentificare a trimițătorului și receptorului, semnătură electronică, calcule securizate.
Cele mai vechi forme de scriere secretizată necesitau doar puțin mai mult decât hârtie și creion (sau unelte similare acestora), întrucât majoritatea oamenilor nu știau să citească. Creșterea alfabetizării a necesitat creșterea complexității criptografiei. Principalele tipuri clasice de cifruri sunt cifrurile cu transpoziție, care modifică ordinea literelor dintr-un mesaj (de exemplu „ajutor” devine „ojartu” într-o schemă trivială de rearanjare), și cifrurile cu substituție, care înlocuiesc sistematic litere sau grupuri de litere cu alte litere și grupuri de litere (de exemplu, „conexiune” devine „dpofyjvof” înlocuind fiecare literă cu următoarea din alfabet). Versiuni simple ale celor două tipuri de cifruri ofereau un grad mic de confidențialitate în cazul oponenților instruiți. Unul din primele cifruri cu substituție a fost Cifrul lui Cezar, în care fiecare literă din textul clar era înlocuită cu o literă aflată la un număr fix de poziții distanță de ea în alfabet. Cifrul a fost denumit astfel după Iulius Cezar despre care se spune că l-a folosit, cu o deplasare de 3, în comunicația cu generalii săi în timpul campaniilor militare.
Criptarea încearcă să asigure secretul comunicațiilor cum sunt cele între spioni, lideri militari, și diplomați, dar a avut și aplicații religioase. De exemplu, vechii creștini foloseau criptografia pentru a ascunde unele aspecte ale scrierilor lor religioase pentru a evita persecuțiile ce i-ar fi așteptat dacă ar fi fost mai puțin atenți; numărul 666 sau, în unele manuscrise mai vechi, 616, Numărul fiarei din Apocalipsă, este uneori considerat a fi o referință la împăratul roman Nero, ale cărui politici includeau persecuția creștinilor.[3] Există și referințe, chiar mai vechi, la anumite cifruri evreiești. Criptografia este recomandată în Kama Sutra ca modalitate a îndrăgostiților de a comunica fără a fi descoperiți.[4] Steganografia (ascunderea existenței mesajului) a fost și ea dezvoltată în antichitate. Unul din primele exemple, de la Herodot, implica ascunderea unui mesaj tatuat pe capul unui sclav ras - sub părul crescut după tatuare.[2] Exemple mai moderne de steganografie includ utilizarea de cerneală invizibilă, micropuncte, și watermarking digital.
Textele cifrate produse de cifrurile clasice (și de unele moderne) dezvăluie informații statistice despre textul clar, care pot fi adesea folosite pentru spargerea acestora. După descoperirea analizei frecvenței (poate de către înțeleptul arab al-Kindi) în preajma secolului al IX-lea, aproape toate aceste cifruri au devenit mai mult sau mai puțin ușor de spart de un atacator informat. Astfel de cifruri clasice încă se bucură astăzi de popularitate, deși mai ales ca jocuri. Aproape toate cifrurile rămân vulnerabile la această tehnică de criptanaliză până la inventarea cifrurilor polialfabetice, de către Leon Battista Alberti în preajma anului 1467 (deși se pare că acesta era cunoscut înainte și de arabi). Inovația lui Alberti a constat în folosirea de cifruri diferite pe părți diferite ale mesajului (la limită, pentru fiecare literă diferită). El a inventat și ceea ce a fost poate primul dispozitiv autinat de cifrare, o roată ce implementa o realizare parțială a invenției sale. În cifrul polialfabetic Vigenère, criptarea se bazează pe un cuvânt cheie, care controlează substituția în funcție de ce literă a cuvântului cheie se folosește. La jumătatea anilor 1800, Charles Babbage a arătat că cifrurile polialfabetice de acest tip rămân vulnerabile la tehnicile de analiză a frecvenței.[2]

Deși analiza frecvenței este o tehnică puternică și generală, criptarea a rămas adesea eficientă în practică; mulți criptanaliști amatori nu stăpânesc această tehnică. Spargerea unui mesaj fără analiza frecvenței necesita cunoașterea cifrului folosit, ceea ce însemna că spargerea acestuia necesita spionaj, mită, dezertări. În cele din urmă, în secolul al XIX-lea, s-a recunoscut explicit că secretul algoritmului unui cifru nu oferă multă siguranță; de fapt, s-a constatat chiar că orice schemă criptografică adecvată (inclusiv cifrurile) trebuie să rămână sigure chiar și dacă adversarul cunoaște perfect algoritmul de cifrare. Secretul cheii ar trebui astfel să fie suficient pentru ca un bun cifru să-și păstreze confidențialitatea în caz de atac. Acest principiu fundamental a fost enunțat explicit în 1883 de Auguste Kerckhoffs și este în general numit Principiul lui Kerckhoffs; el a fost reenunțat mai succint și mai direct de Claude Shannon ca Maxima lui Shannon — „Inamicul cunoaște sistemul”.
Diferite dispozitive fizice au fost folosite pentru a ajuta lucrul cu cifrurile. Una din primele modalități a fost scytalul din Grecia antică, un sul folosit probabil de spartani ca ajutor la criptarea și decriptarea cu un cifru cu transpoziție. În epoca medievală, au fost inventate și alte unelte, cum ar fi grila de cifru, folosită și pentru un fel de steganografie. Inventarea cifrurilor polialfabetice, a declanșat inventarea unor unelte mai sofisticate, cum ar fi discul lui Alberti, schema cu tabula recta a lui Johannes Trithemius, și multicilindrul lui Thomas Jefferson (reinventat independent de Étienne Bazeries pe la 1900). Unele aparate mecanice de criptare/decriptare au fost inventate la începutul secolului al XX-lea, printre care s-au numărat mașinile rotitoare — cea mai celebră fiind mașina Enigma folosită de Germania în al doilea război mondial. Cifrurile implementate de mașini similare dar îmbunătățite au adus o creștere a dificultății criptanalizei după al doilea război mondial.[5]
Dezvoltarea electronicii și a calculatoarelor numerice după al doilea război mondial au făcut posibile cifruri mult mai complexe. Mai mult, calculatoarele au permis criptarea oricărui fel de date reprezentate de calculator în format binar, spre deosebire de cifrurile clasice care criptau doar texte în limbaj scris, dizolvând utilitatea abordării lingvistice a criptanalizei în multe cazuri. Multe cifruri informatice pot fi caracterizate prin operarea pe secvențe de biți (uneori pe grupuri sau blocuri), spre deosebire de schemele clasice și mecanice, care manevrează caractere tradiționale (litere și cifre) direct. Totuși, calculatoarele au ajutat și criptanaliștii, ceea ce a compensat până la un punct creșterea complexității cifrurilor. Cu toate acestea, cifrurile moderne bune au rămas cu un pas înaintea criptanalizei; este cazul de obicei ca utilizarea unui cifru de calitate să fie foarte eficientă (rapidă și puțin costisitoare în ce privește resursele), în timp ce spargerea cifrului să necesite un efort cu multe ordine de mărime mai mare, făcând criptanaliza atât de ineficientă și nepractică încât a devenit efectiv imposibilă.
Cercetările academice deschise desfășurate în domeniul criptografiei sunt relativ recente — au început doar la jumătatea anilor 1970 cu specificațiile publice ale DES (Data Encryption Standard) la NBS, lucrarea Diffie-Hellman,[6] și publicarea algoritmului RSA. De atunci, criptografia a devenit o unealtă folosită pe scară largă în comunicații, rețele de calculatoare, și în securitatea informatică în general. Nivelul prezent de securitate al multor tehnici criptografice moderne se bazează pe dificultatea unor anumite probleme computaționale, cum ar fi problema factorizării întregilor sau a calculului logaritmilor discreți. În multe cazuri, există demonstrații matematice care arată că unele tehnici criptografice sunt sigure dacă o anumită problemă computațională nu poate fi rezolvată eficient.[7]
Proiectanții de sisteme și algoritmi criptografici, pe lângă cunoașterea istoriei criptografiei, trebuie să ia în considerație în dezvoltarea proiectelor lor și posibilele dezvoltări ulterioare. De exemplu, îmbunătățirile continue în puterea de calcul a calculatoarelor au mărit gradul de acoperire al atacurilor cu forța brută la specificarea lungimii cheilor. Efectele potențiale ale calculatoarelor cuantice sunt deja luate în calcul de unii proiectanți de sisteme criptografice; iminența anunțată a implementării acestor mașini face aceste precauții necesare.[8]
În principal, până la începutul secolului al XX-lea, criptografia s-a ocupat mai ales de șabloane lingvistice. De atunci, accentul s-a mutat pe folosirea extensivă a matematicii, inclusiv a aspectelor de teoria informației, complexitatea algoritmilor, statistică, combinatorică, algebră abstractă și teoria numerelor. Criptografia este și o ramura a ingineriei, dar una neobișnuită, întrucât se ocupă de opoziția activă, inteligentă și răuvoitoare; majoritatea celorlalte ramuri ale ingineriei se ocupă doar de forțe naturale neutre. Se fac cercetări și în examinarea relațiilor dintre problemele criptografice și fizica cuantică.
Criptografia modernă
Domeniul modern al criptografiei poate fi împărțit în câteva domenii de studiu. Cele principale sunt discutate aici.
Criptografia cu chei simetrice
Criptografia cu chei simetrice se referă la metode de criptare în care atât trimițătorul cât și receptorul folosesc aceeași cheie (sau, mai rar, în care cheile sunt diferite, dar într-o relație ce la face ușor calculabile una din cealaltă). Acest tip de criptare a fost singurul cunoscut publicului larg până în 1976.[6]
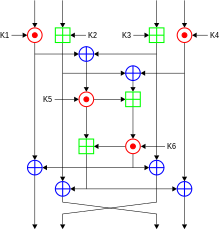
Studiul modern al cifrurilor cu chei simetrice se leagă mai ales de studiul cifrurilor pe blocuri și al cifrurilor pe flux și al aplicațiilor acestora. Un cifru pe blocuri este, într-un fel, o formă modernă de cifru polialfabetic Alberti: cifrurile pe blocuri iau la intrare un bloc de text clar și o cheie, și produc la ieșire un bloc de text cifrat de aceeași dimensiune. Deoarece mesajele sunt aproape mereu mai lungi decât un singur bloc, este necesară o metodă de unire a blocurilor succesive. S-au dezvoltat câteva astfel de metode, unele cu securitate superioară într-un aspect sau altul decât alte cifruri. Acestea se numesc moduri de operare și trebuie luate în calcul cu grijă la folosirea unui cifru pe blocuri într-un criptosistem.
Data Encryption Standard (DES) și Advanced Encryption Standard (AES) sunt cifruri pe blocuri care sunt considerate standarde de criptografie de guvernul american (deși DES a fost în cele din urmă retras după adoptarea AES).[9] În ciuda decăderii ca standard oficial, DES (mai ales în varianta triple-DES, mult mai sigură) rămâne încă popular; este folosit într-o gamă largă de aplicații, de la criptarea ATM[10] la securitatea e-mail-urilor[11] și accesul la distanță securizat.[12] Multe alte cifruri pe blocuri au fost elaborate și lansate, cu diverse calități. Multe au fost sparte.[8][13]
Cifrurile pe flux de date, în contrast cu cele pe blocuri, creează un flux arbitrar de material-cheie, care este combinat cu textul clar, bit cu bit sau caracter cu caracter. Într-un cifru pe flux de date, fluxul de ieșire este creat pe baza unei stări interne care se modifică pe parcursul operării cifrului. Această schimbare de stare este controlată de cheie, și, la unele cifruri, și de fluxul de text clar. RC4 este un exemplu de binecunoscut cifru pe flux.[8]
Funcțiile hash criptografice (adesea numite message digest) nu folosesc neapărat chei, sunt o clasă importantă de algoritmi criptografici. Aceștia primesc date de intrare (adesea un întreg mesaj), și produc un hash scurt, de lungime fixă, sub forma unei funcții neinversabile. Pentru hash-urile bune, coliziunile (două texte clare diferite care produc același hash) sunt extrem de dificil de găsit.
Vezi și
- Cod
- Criptare
- Criptogramă
- Criptomonedă
- Istoria criptologiei
- Istoria criptanalizei
- Pătratul lui Polybius
- Scytal
- Temura
Note
- ^ Academia Română, Dicționarul explicativ al limbii române, Editura Univers Enciclopedic Gold, 2016
- ^ a b c d David Kahn, The Codebreakers, 1967, ISBN 0-684-83130-9.
- ^ Eerdmans Commentary on the Bible, James D G Dunn, John W Rogerson, eds., Wm. B. Eerdmans Publishing, 2003, ISBN 0-8028-3711-5
- ^ Kama Sutra, Sir Richard F. Burton, translator, Partea I, Capitolul III, artele 44 și 45.
- ^ James Gannon, Stealing Secrets, Telling Lies: How Spies and Codebreakers Helped Shape the Twentieth Century, Washington, D.C., Brassey's, 2001, ISBN 1-57488-367-4.
- ^ a b Whitfield Diffie și Martin Hellman, "New Directions in Cryptography", IEEE Transactions on Information Theory, vol. IT-22, Nov. 1976, pp: 644–654. (pdf)
- ^ Oded Goldreich, Foundations of Cryptography, Volume 1: Basic Tools, Cambridge University Press, 2001, ISBN 0-521-79172-3
- ^ a b c AJ Menezes, PC van Oorschot și SA Vanstone, Handbook of Applied Cryptography ISBN 0-8493-8523-7.
- ^ FIPS PUB 197: The official Advanced Encryption Standard Arhivat în , la Wayback Machine..
- ^ NCUA letter to credit unions Arhivat în , la Wayback Machine., iulie 2004
- ^ RFC 2440 - Open PGP Message Format
- ^ SSH at windowsecurity.com Arhivat în , la Wayback Machine. de Pawel Golen, iulie 2004
- ^ Bruce Schneier, Applied Cryptography, 2nd edition, Wiley, 1996, ISBN 0-471-11709-9.
Bibliografie
- Simon Singh - How to Make It, Break It, Hack It, Crack It, Delacorte Press, New York 2001
- David Kahn - The Codebreakers, New York 1996
- S. McClain - The Navajo Weapon, Boulder, Colorado 1994
- Simson Garfinkel - PGP: Pretty Good Privacy, Bonn 1996
- James Bamford - The Puzzle Palace, London 1983 (despre NSA)
Legături externe
- Criptografia și codurile secrete care au marcat istoria, 13 septembrie 2012, Maria Olaru, Descoperă
- BerkaEnigma - Criptografía Simétrica Aplicada
| Istoria criptologiei | Criptanaliză | Portalul criptografiei | Subiecte în criptografie |
| Algoritm cu chei simetrice | Cifru bloc | Cifru stream | Criptografie cu chei publice | Funcție hash criptografică | Cod de autentificare a mesajelor | Număr aleatoriu |