Teorema lui Desargues
În geometria euclidiană, teorema lui Desargues este o problemă de geometrie sintetică.
Enunț
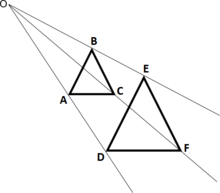
Fie două triunghiuri ΔABC și ΔDEF fără vârfuri comune, cu laturi respectiv paralele. Atunci dreptele AD, BE și CF sunt paralele sau concurente.
Soluție
2) În cazul în care segmentele AB și DE sunt egale, ABDE este un paralelogram. De aici rezultă AD || BE. Tot din AB = DE rezultă egalitatea triunghiurilor ΔABC = ΔDEF deci și a segmentelor BC și EF. Ca și mai înainte, vom avea BE || CF. În concluzie, AD || BE || CF .
1) În cazul în care segmentele AB și DE au lungimi diferite, dreptele AD și BE se vor întâlni într-un punct O. (În caz contrar, ar rezulta că ABDE ar fi un paralelogram ceea ce contravine ipotezei)
OD/OA = DE/AB
Tot în acest caz, triunghiurile ΔABC și ΔDEF sunt asemenea, fără a fi egale :
DE/AB = EF/BC ≠ 1
Fie acum O' punctul de intersecție al dreptelor BE și CF.
Avem O'E/O'B = EF/BC = DE/AB = OE/OB. Va rezulta :
OE/OB - 1 = O'E/O'B - 1, apoi EB/OB = EB/O'B și deci
OB = O'B.
Dacă luăm în compas lungimea BO, ridicăm compasul, punem la loc un vârf în B și trasăm punctul O', acesta va coincide cu punctul de plecare O, așadar
O = O' iar dreptele date sunt concurente. Q.E.D.
Soluția 3D
Desenul reprezintă de fapt situația văzută de sus, iar ABC este de fapt o prismă dreaptă văzută de sus. Să notăm partea superioară a prismei cu A”B”C”. Segmentele paralele
- A”B” și DE,
- A”C” și DF,
- B”C” și EF determină trei plane care se vor intersecta într-un punct O”. (dacă nu, cădem peste cazul 2) și aplicăm soluția 2D).
Proiecția dreaptă a acestui punct pe planul desenului este traversată de toate cele trei proiecții ale celor trei drepte de intersecție ale celor trei plane. Altfel spus, dreptele considerate inițial sunt proiecții ale unor drepte concurente, și deci sunt concurente.
Comentariu

În geometria proiectivă cele două cazuri 1) și 2) sunt unificate, prin adăugarea punctelor, dreptelor, sau planelor „de la infinit”.
Vezi și
Pentru alte probleme care au soluții cu triunghiuri asemenea,
Manuale
- Michèle Audin, Géométrie, EDP Sciences, 2006