Градиент концентрации
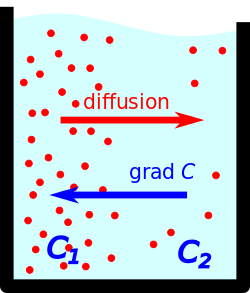

Градиент концентрации или концентрационный градиент — векторная физическая величина, характеризующая величину и направление наибольшего изменения концентрации какого-либо вещества в среде. Например, если рассмотреть две области с различной концентрацией какого-либо вещества, разделённые полупроницаемой мембраной, то градиент концентрации будет направлен из области большей концентрации вещества в область с меньшей его концентрацией. Вектор диффузионного потока направлен против вектора градиента концентрации, что, в соответствии с принципом Ле Шателье, приводит со временем к уменьшению этого потока и градиента концентрации.
Определение
Градиент концентрации направлен по пути , соответствующему нормали к изоконцентрационной поверхности (полупроницаемой мембране). Значение градиента концентрации равно отношению приращения концентрации к соответствующему приращению пути :
При постоянном значении градиента концентрации на длине пути :
Здесь и — начальное и конечное значение концентрации на длине пути (нормали к изоконцентрационной поверхности).
Градиент концентрации может быть причиной переноса веществ, например диффузии. Согласно закону Фика, диффузионный поток, то есть количество молекул рассматриваемого типа, проходящих при диффузии через единичную площадку, перпендикулярную к градиенту концентрации, в единицу времени, определяется выражением:
- ,
где n — концентрация молекул рассматриваемого типа, D — коэффициент диффузии. Таким образом, диффузия осуществляется против вектора градиента концентрации[1][2].
Единицей измерения градиента концентрации в Международной системе единиц (СИ) является величина м−4 (моль/м4 или кг/м4), а также её дольные или кратные производные.
См. также
Примечания
- ↑ Сивухин Д. В. § 91. Самодиффузия в газах // Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2005. — Т. II. Термодинамика и молекулярная физика. — С. 344. — 544 с. — ISBN 5-9221-0601-5.
- ↑ Кикоин А. К., Кикоин И. К. Молекулярная физика. — М.: Наука, 1976. — С. 146. — 480 с.
Литература
- Антонов В. Ф., Черныш А. М., Пасечник В. И. Биофизика — М.: ВЛАДОС, 2000, С. 35. ISBN 5-691-00338-0
- Трифонов Е. В. Психофизиология человека, 14-е изд. — СПб.: 2011.









