वर्नियरमापकम्
सामान्येन मीटरमापकोपकरणेन वयं दृष्ट्या अवलोक्य २ मिलीमीटरपर्यन्तस्य अनुमानेन च तदर्घभागपर्यन्तस्य दैर्घ्यं मापितुं शक्नुमः । परन्तु, तदग्रेऽनुमातुम् आस्माकीना दृष्टिरसमर्थंव । अतएव दैर्घ्यस समधिकरूपेण विशुद्धतया मापनार्थं वर्नियर्, चूलिकामापकः, (Screw gauge) वृत्तमापकादीनि यन्त्रणि विनिर्मितानि ।
सप्तदशे स्वीष्टाब्दे फ्रान्सदेशीयेन पीरेवर्नियरनामकेन गणितज्ञेन वर्नियरनामकं यन्त्रम् आविष्कृतम् ।अतएव तन्नाम्नैव अभिहितमिदं यन्त्रम् । इदं वर्नियरमेकः सहायकः मापकः भवति । स मुख्यमापके अभिसरति । मुख्यमापकवत् वर्नियरमपि चिह्नाङ्कितं भवति । परन्तु तानि चिह्नानि इत्थम् अङ्कितानि भवन्ति यत् वर्नियरस्य ’न’ चिन्हानां दैर्घ्यं प्रायशः मुख्यमापिकायाः (न-१) चिन्हानां दैर्घ्यतुल्यं कदाचिञ्च (न+१) चिन्हानां दैर्घ्यतुल्यं भवति। ते दैर्घ्यं मुख्यमापिकायाः ६ भागतुल्याः भवन्ति । अत एकस्य मुख्यमापिकाभागस्य वर्नियरभागस्य च अन्तरः १/१० मुख्यमापिकाभागतुल्यो भवति । परन्तु इञ्चाङ्कितेषु कतिषु वर्नियरेषु ८ भागाः मुख्यमापिकायाः ६ भागरुल्याः भवन्ति, तदा तु मुख्यमापिकायाः इञ्चपरिमित्यां १६ भागाः भवन्ति । कदाचित्तु वर्नियरस्य २० भागाः मुख्यमापिकायाः १६ भागातुल्या: भवन्ति ।
१.३ चित्रे मुख्यमापिका वर्नियरञ्च युगपद् प्रदर्शिते । वर्नियरस्य १० भागानां दैर्घ्यं मापिकायाः ६ भागतुल्यम् अस्ति । वर्नियरस्य शून्यचिन्हं मापिकायाः शून्यचिन्हस्य अभिमुखं वर्त्तते । परन्तु वर्नियरस्य इतराणि चिन्हानि मापिकायाः चिन्हापेक्षया वामपार्श्वे अपसृतानि । तथा च :- १ मुख्यमापिकाभागस्य १ वर्नियरभागस्य चान्तरः = १/१० मापिकाभागः २ मुख्यमापिकाभागस्य २ वर्नियरं भागस्य चान्तरः = २/१० मापिकाभागः ३” ३” = ३/१० मापिकाभागः इत्यादयः
अन्ततोगत्वा वर्नियरस्य दशमे भागे मापिकायाः दशमे भागे च पूर्णतया एकमापिका भागेन तुल्योऽन्तरं भवति। अर्थात् स मापिकायाः नवमचिन्हस्य अभिमुखं भवति । इत्थं तद्यपि एकमापिकाभागस्य ततोऽन्ये लघुभागाः विहिताः तथापि – वर्नियरस्य साहाय्येन तस्य १/१०, २/१०, ३/१० प्रभृतीनां भागानां दैर्घ्यं याथार्थेन लक्ष्यते अस्यां दशायां न्यूनतमं पठनीयं दैर्घ्यं १/१० मापिकाभागस्य तुल्यं भवति दैर्घ्यमिदं वर्नियरस्य लघुतमः मापः (Least count) इत्यभिघीयते । अतः कस्यचिद् वर्नियरस्य लघुतमः मापः मुख्यमापिकायाः १ भागस्य यद्-दैर्घ्यं वर्नियरस्य १ भागस्य च यद् दैर्घ्यं तयोरन्तरेण तुल्यः भवति । अयमेव अन्तरः वर्नियराल्पतमाङ्कोऽपि ( vernier constant) कथ्यते ।
वर्नियरस्य पठनाय प्रथमं वर्नियरस्य शून्यतः पूर्ववर्त्तीनि मुख्यमापिकाचिन्हानि पठनीयानि । तदनन्तरं वर्नियरं वर्नियरे स्वचक्षुचालनं कुर्वन् अवलोकनीयं यत् वर्नियरस्य कतमं चिन्हं मुख्यमापिकाचिन्हाभिमुखं वर्तते । संख्यां चेमं वर्नियरस्य अल्पतमाङ्केन गुणयित्वा मुख्यमापिकायाः मापे संयोजनात् पूर्णमापः परिज्ञायते ।
वर्नियरकैलिपर्सं (vernier calipers) तस्य प्रयोगश्च
यस्मिन् सामान्यतमे यन्त्रे, वर्नियरस्य उपयोगः क्रियते तद् वर्नियरकैलिपर्समिति नाम्ना अभिधीयते । अस्मिन् यन्त्रे मुख्यमापिका एकायस्पट्टिकोपरि निर्मिता भवति । तत्र एकस्मिन् पर्श्वे इञ्चं तस्य दशमो भागः कदाचिञ्च षोडशो भागोऽङ्कतो भवति । तत्र एकस्मिन् पर्श्वे इञ्चं तस्य दशमो भागः कदाचिञ्च षोडशो भागोऽङ्कतो भवति । वर्नियरमापकं च तदुपरि प्रसरन्त्यां एकस्यां अन्यासां अयस्पट्टिकायाम् अङ्कितं भवति ।
प्रायशः वर्नियरमापिकायाः दश भागाः दैर्घ्यं मुख्यमापिकायाः नवभागतुल्याः भवन्ति । मुख्यमापिकायाः वर्नियरस्य वामपार्श्वस्य शिरसी च द्वयोरन्ययो पट्टिकयोर् दैर्घ्यंण सह समकोणं विदघती संयुक्त्ते भरतः । अ, ब इति शिरसी वाह्यपिण्डं परिमातुं, स, द कस्यचिद् रिक्त्तान्तरस्य वस्तुनः आन्तरिकं व्यासं परिमातुं, पट्टिका ’य’ च गभीरत्वं परिमातुं भवाति। यदा इमे पट्टिके पूर्णतया अन्योन्यं स्पृशतः तदा मुख्यमापिकायाः वर्नियरस्य च शून्यचिन्हे सर्वथैव अभिमुखीने न भवतः अपितु तयोर्मघ्ये किञ्चिदन्तिरी भवति । उभयोः शून्ययोरन्तरश्चाय शून्याङ्की त्रुटिरिति (Zero Error) कथ्यते । अयन्तु वर्नियरसाहाय्येन पठ्यते । वर्नियरकैलिपर्सेन मापनारम्भाद् पूर्वं शून्याङ्कित्रुट्याः पठनम् अन्यावश्यकं भवति ।
प्रयोगकरणस्य रीतिः
प्रयोगकरणस्य रीतिः भागत्रये विभाज्या
१. वर्नियरस्य अल्पतमाङ्कस्य ज्ञानकरणम् ।
२.शून्याङ्कित्रुट्याः ज्ञानकरणम् ।
३. प्रदत्तस्य दैर्घ्यस्य मापनम् ।
वर्नियरस्य अल्पतमाङ्कस्य ज्ञानकरणम्
वर्नियराल्पतमाङ्कस्य ज्ञानकरणार्थम् उभयोर्मापिकयोः शून्ये परस्पराभिमुखोने कृत्वा लक्ष्यते यत् वर्नियरस्य कियद्भागानां दैर्घ्यं मुख्यमापिकायाः किपद्भागानां दैर्घ्येण तुल्यं अस्ति । अनेन प्रकारेण गणनाद्वारा मुख्यमापिकाया एकस्य भागस्य वर्नियरस्य च स च यद् दैर्घ्यस्य अन्तरः अर्थात् वर्नियरस्य अल्पतमाङ्कः परिज्ञायते ।
शून्याङ्कित्रुट्याः ज्ञानकरणम्
शून्याङ्किकीं त्रुटिं परिज्ञातुं मापिकयोरुभयोः पट्टिके सर्वथैव संयुज्येते पुनश्च अवलोक्यते यत् मापिकयोरुभयोः शून्ये परस्पराभिमुखीने स्तः न वा । यदि चेदुभे शून्ये अभिमुखीने स्तः तर्हि उपकरणे कापि शून्याङ्किकी त्रुटिनं भवति । यदि वर्नियरस्य शून्यं मुख्यमापिकायाः शून्यतोऽग्रे भवति तर्हि शून्याङ्की त्रुटिः घनात्मिका भवति सा च प्रेक्षणेभ्यः ऊनीकरणीया यदि चेत् वर्नियरस्य शून्यं पश्चाद् वर्त्तते तर्हि शून्याङ्किकी त्रुटिः श्रृणात्मिका भवति सा च प्रेक्षणेषु संयोज्या भवति । अघस्यनयोः चित्रयोः कल्पनीयं यत् मुख्यमापिका मि.मी. इति परिमाणेन विभाजिता तथाच वर्नियरस्य अल्पतमाङ्कः ०१ से.मी. परिमितोऽस्ति ।
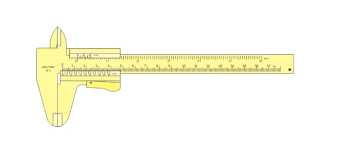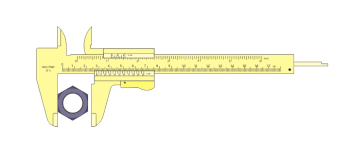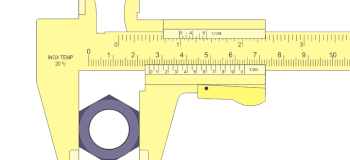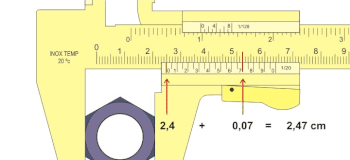
वर्नियरपठनसम्बन्धिसामान्यनियमानुसारेण दक्षिणभागतः पठने वर्नियरस्य ’स’ इति तृतीयं चिन्हं मुख्यमापिकायाः नवमचिन्हतः १ से.मी.+०३ से.मी. =१३ से.मी. वामभागेऽपसृतम् भवति । दैर्घ्यमिदं वर्नियरस्य यत् शून्यं मुख्यमापिकायाश्च यत् शून्यं तयोर्मघ्यवर्त्तिना दैर्घ्येण तुल्यं भवेत् । यतः यदा वर्नियरस्य शून्यं मुख्यमापिकायाः शून्यस्य अभिमुखं भवेत् तर्हि वर्नियरस्य दशमं चिन्हं मुख्यमापिकायाः मवमचिन्हस्य अभिमुखं वर्तते ।
अतएव ऋणात्मिका शून्याङ्किकी त्रुटिः=१३ से.मी. । प्रेक्षणेषु इयं संयोजनीया ।
प्रदत्तस्य दैर्घ्यस्य मापनम्
यस्य वस्तुनः दैर्घ्यं वर्नियरकैलिपर्सेन मापनीयं भवति तत्तु द्वयोः पट्टिकयोर्मघ्ये तथा गृह्यते यत् ते तद्वस्तु सम्यक्तया स्पृशेताम् । अथात् यन्त्रेण वस्तुनः ग्रहणकाले तद्वस्तु नैव शिथिलं न चाप्यतिदिढं भवेत् । पुनश्च अवलोक्यते यत् वर्नियरस्य शून्यचिन्हं मापिकायाः कस्मात् चिन्हाद् अग्रे वर्त्तते । अस्य चिन्हस्य पठनात् मुख्यमापिकायाः मानं परिज्ञायते । तदनन्तरं स्वचक्षुषो युगपदेव उभयोर्मापिकयोः दक्षिणभागे निक्षिप्य परिलक्ष्यते यत् वर्नियरस्य कतमं चिन्हं याथार्थेन मुख्यमापिकायाः कस्य चिन्हस्य अभिमुखं वर्त्तते । वर्नियरस्यास्य चिन्हस्य संख्या वर्नियरस्य अल्पतमाङ्केन गुण्यते । इत्यं वर्नियरस्य मापो लभ्यते ।
यदि चेत् इञ्चपरिमाणे सेण्टीमीटराणां संख्या उपलभ्या तर्हि इञ्चेषु सेण्टीमीटरेषु च शून्याङ्की त्रुटिं परिलक्ष्य वर्नियरकैलीपर्सं विभिन्नदैर्घ्ये प्रसार्य तानि दैर्घ्याणि इञ्चेषु सेन्टीमीटरेषु च पठनीयानि ।प्रत्येकस्य दैर्घ्यस्य सेण्टीमीटरस्य संख्या यदि इञ्चानां संख्या विभज्यते तर्हि एकस्मिन् इञ्चे सेण्टीमीटरस्य संख्या उपलभ्यते । अष्टवारं दशवारं वा ईदृशं प्रेक्षणं कृत्वा तस्य मघ्यमं मानं ज्ञातव्यम् । अत्र समविकस्य दैर्घ्यस्य ग्रहणात् शुध्दत्वमं फलं ज्ञायते (कथम् ?) ।
यदि चेत् कस्यचिद् सघनवलयकण्डस्य आयतनं माप्यं तर्हि तस्य उच्छितिः व्यासश्च वर्नियरकैलिपर्सेण मापनीयो । व्यासं च अर्ध्दीकृत्य त्रिज्यायाः दैर्घ्यं ’त्र’ इति ज्ञातव्यम् । पुनश्च आयतनम् = π × त्र२ × उच्छ्रिति इति सूत्रेण आयतनं गणनीयम् ।
यदि चेत् कस्यचिद् रिक्तान्तरस्य वलयदण्डस्य आभ्यन्तरम् आयतनं ज्ञातव्यं स्यात् तर्हि वलयदण्डस्य गभीरत्वमं ’य’ इति पट्टिकया तस्याभ्यन्तरं व्यासं च वर्नियरकैलिपर्सस्य ’स’ द’ इति शिरोभ्यां माप्यते । व्यासस्य अर्ध्दं त्रिज्या भवति । पुनश्च आयतनम् = π त्र२ × गाम्भीर्यम् इति सूत्रेण गणना क्रियते ।
अवधानीयम्
- दैर्घ्यमापनकाले वस्तु इत्थं ग्राह्यं यत् तत् पट्टिकयोर्मघ्ये सम्यक्तया स्थितं भवेत । इदम् गृहीतं वस्तु अतिदृढं शिथिलं दा न भवेत् ।
- वलयदण्डस्य यथार्थं व्यासं परिज्ञातुं प्रत्येकस्मिन् स्थाने द्वयोः लम्वरूपयोः दिशोः मापः करणीय; (किम् ?) । ईदृशश्च मापः कतिपयेषु च स्थानेषु ग्राह्यः ।
वर्नियरकैलिपर्सेण क्रियमाणा इतरे प्रयोगाः
प्रयोगद्वारा ’π’ इत्यस्य मानस्य ज्ञानम्
कस्यचिद् वृत्तस्य परिधेः दैर्घ्यं तस्य व्यासस्य दैर्घ्यापेक्षया यावद्गुणितमधिकं भवति तदनुपातः ’π’ इति ग्रीकाक्षरेण लक्ष्यते । ’π’ चिन्ह्मिदं पादिकानाम्नाभिहितम् । पादिकायाः मानं परिज्ञातुं निम्नाङ्कितयोः रीत्योः कतरापि रीतिः प्रयोज्या । किन्तु, तत्रायमेव सिध्दान्तो निहितः यत् परिधेः व्यासस्य च दैर्घ्यम् उपलभ्य व्यासदैर्घ्येण परिधिदैर्घ्यं विभज्यते ।
प्रथमा रीतिः
विभिन्नानां व्यासानां चत्वारः पञ्च वा वलयदंडाः संगृह्याः । तेपां परिधयः एकेन ऋज्वा सूक्ष्मसुत्रेण व्यासाश्च वर्नियरकैलिपर्सेण मापनीयाः । प्रत्येकस्य परिधेश्च दैर्घ्यं तस्य व्यासदैर्घ्येंण विभाज्यम् । इत्थं ’π’ इत्यस्य अर्थात् पदिकायाःमानम् उपलभ्यते । सर्वेषां मानानां योगं प्रेक्षणसंख्यया विभजनात् ’π’ इत्यस्य अर्थात् पादिकायाः मध्यमं मानं ज्ञायते ।
द्वितीया रीतिः
कर्गदस्य सूक्ष्मैकां पट्टिकां आदाय तस्यैका आवृत्तिः वलयदंडोपरि इत्थं आस्तरणीया यत् कर्गदेन वलयदंडः पूर्णतया स्पृष्टो भवेत् । यत्र कर्गदस्य उभे शिरसी ऊर्घ्वाधरं वर्त्तेते तत्र कीलिकया छिद्रयोरुभयोर् ’अ’-’ब’ इत्येतयोर्मघ्यस्यितं दैर्घ्यं मापनीयम् व्यासः मापनीयः । व्यासदैर्घ्येण च परिघिदैर्घ्यं भाज्यम् । तर्हि ’π’ इत्यस्य अर्थात् पादिकायाः मानं ज्ञायते । मानञ्चे दं २२/७ अथवा ३.१४ इत्यनेन तुल्यं भवति ।
प्रदत्तस्यैकस्य अनुप्रस्थपरिच्छेदस्य क्षेत्रफलं ज्ञातव्यम्
क्षेत्रफलम् = π त्र२ । यत्र ’त्र’ इति वलयदण्डस्य त्रिज्या भवति ।
प्रदत्तस्यैकस्य वलयदण्डस्य आपयतनं मापिकागलपात्रिकया (Measuring glass) ज्ञातव्यं साधनीयञ्च यत् आयतनं = π त्र२ च यत्र ’त्र’ इति परिच्छेदस्य त्रिज्या तथा ’च’ इति वलयदण्डस्य उच्र्छितिरस्ति ।