Delta v
| Del niza o področju |
| Astrodinamika |
|---|
 |
|
Inženiring in učinkovitost |
Delta v [délta vé] (dobesedno sprememba hitrosti, tudi karakteristična hitrost orbitalnega manevra), označena kot ∆v, je v astrodinamiki in raketodinamiki količina, ki se rabi pri dinamiki poletov vesoljskih plovil, in je mera za potrebni sunek sile, da plovilo izvede manever (spremembo tira), kot je na primer izstrelitev ali pristanek na planetu ali luni, ali orbitalni manever v vesoljskem prostoru. Je skalarna količina in ima enoto hitrosti m·s−1. Rabljena v tem kontekstu se razlikuje od fizikalne spremembe hitrosti plovila.
Kot preprosti zgled je lahko običajna raketa, ki z izgorevanjem goriva dosega potisk. Delta v je sprememba njene hitrosti, ki jo lahko doseže z izgoretjem svojega celotnega goriva.
Delto v ustvarjajo reakcijski motorji, kot so na primer raketni motorji in je sorazmerna s potiskom na enoto mase in časom izgorevanja. Rabi se za določevanje mase raketnega potisnega goriva, ki je potrebno za dani manever prek enačbe Ciolkovskega.
Pri mnogokratnih manevrih se delta v sešteva linearno.
Za medplanetarne odprave se delta v velikokrat izriše na konturnem grafu svinjske zarebrnice (porkchop plot), ki prikazuje odvisnost zahtevane delte v za odpravo od datuma izstrelitve.
Definicija
Delta v se lahko izrazi z naslednjim integralom:
kjer je:
- – trenutni potisk motorja ob času ,
- – trenutna masa plovila ob času ,
- – začetni čas izgorevanja,
- – končni čas izgorevanja.
Posebni primeri
Če ni zunanjih sil, velja enačba:
kjer je koordinatni pospešek.
Če deluje potisk v isti smeri, je izraz v/|v| konstanten, in enačba se poenostavi v:
kar je preprosto velikost spremembe hitrosti. Ta zveza pa v splošnem ne velja. Če se na primer konstantni enosmerni pospešek po času (t1 − t0)/2 obrne, je razlika hitrosti enaka 0, delta v pa je za neobrnjeni potisk enaka.
Za rakete 'na katere ne delujejo zunanje sile' je mišljeno, da na njih ne deluje gravitacija, upor ozračja, aerostatični protitlak na šobo in elektromagnetna polja so šibka, tako da se za izračun zmogljivosti delte v plovila prek enačbe Ciolkovskega rabi vakuumski specifični sunek Isp, stroški za izgube v ozračju pa se prevalijo v zalogo delte v pri izstrelitvah s planetovega površja.
Orbitalni manevri
Orbitalni manevri se izvajajo z zagonom potisnika, ki proizvede reakcijsko silo delujočo na vesoljsko plovilo. Velikost te potisne sile je enaka:
kjer je:
- – efektivna hitrost izhajanja izpušnega plina v raketnem okvirju,
- – velikost masnega toka potisnega goriva v izgorevalni komori.
Pospešek vesoljskega plovila, ki ga povzroča ta sila, je enak:
kjer je masa vesoljskega plovila.
Med izgorevanjem se masa vesoljskega plovila manjša zaradi porabe goriva, njen časovni odvod pa je enak:
Če je sedaj smer sile, to je smer šobe, med izgorevanjem stalna, se hitrost zaradi potisne sile izgorevanja od začetnega časa do končnega časa poveča za:
Če se namesto integracijske spremenljivke časa vzame masa vesoljskega plovila , velja:
Pri tem se privzame, da je konstanta in ni odvisna od količine preostalega goriva. Ta zveza se tako integrira v:
kar je enačba Ciolkovskega.
Če na primer 20 % začetne izstrelitvene mase predstavlja gorivo, ki da konstantno efektivno izpušno hitrost 2100 m/s (tipična vrednost hidrazinskega potisnika), je zmogljivost takšnega reaktivnega nadzornega sistema (RCS) enaka:
Če ni konstantna funkcija količine preostalega goriva:[a]
se zmogljivost reakcijskega nadzornega sistema izračuna z zgornjim integralom.

Pospešek, ki ga povzroča potisna sila je le dodatni pospešek, ki ga je treba prišteti k drugim pospeškom (sili na enoto mase), ki vplivajo na vesoljsko plovilo, tako da se lahko tir razširi z numeričnim algoritmom, ki vključuje tudi to potisno silo.[b] Za mnoge namene, tipično za raziskave optimizacije manevrov, se aproksimirajo s sunkovnimi manevri, kot je prikazano na sliki z po zgornji enačbi. Poleg tega se lahko na primer vzame pristop modeliranja manevra s »stožčevimi zaplatami« (patched conics) kot premik z enega Keplerjevega tira na drugega s trenutno spremembo vektorja hitrosti.
Ta aproksimacija s sunkovnimi manevri je v večini primerov zelo točna, vsaj kadar se rabi kemijsko gorivo. Za nizkopotisne sisteme, tipično na primer za električne pogonske sisteme, je ta aproksimacija manj točna. Tudi za geostacionarno vesoljsko plovilo, ki rabi električni pogon za zunanjravninski nadzor izgorevanja potisnika s periodami več ur okrog vozlov, je takšna aproksimacija zadovoljiva.
| vrsta manevra | potrebna Δv [m/s] | ||
|---|---|---|---|
| srednja | največja | ||
| kompenzacija upora ozračja na višini orbite ... |
400–500 km | < 25 | < 100 |
| 500–600 km | < 5 | < 25 | |
| > 600 km | < 7,5 | ||
| nadzor lege plovila (po treh oseh) na orbiti | 2–6 | ||
| zadrževanje plovila v legi na GSO | 50–55 | ||
| zadrževanje plovila v Lagrangeevih točkah L1/L2 | 30–100 | ||
| zadrževanje plovila v Lunini orbiti[1] | 0–400 | ||
Proizvodnja
Delto v običajno zagotovi potisk raketnega motorja, lahko pa jo proizvedejo drugi motorji. Časovni prirastek spremembe delte v je velikost pospeška, ki ga proizvedejo motorji, to je potisk na skupno maso plovila. Dejanski vektor pospeška se določi z dodajanjem potiska na maso k vektorju gravitacije in vektorjem, ki predstavljajo druge sile delujoče na telo.
Za skopno delto v je potrebna dobra začetna točka pri zgodnjih odločitvah konstrukcije, saj se upoštevanje dodatnih kompleksnosti odlaša na kasnejši čas konstrukcijskega procesa.
Enačba Ciolkovskega kaže, da se zahtevana količina pogonskega potisnega goriva z naraščajočo delto v zelo poveča. Zato se pri sodobnih sistemih pogonov vesoljskih plovil precej raziskuje zmanjšanje skupne delte v, potrebne za dani vesoljski polet, kot tudi konstruiranje vesoljskih plovil, zmožnih proizvodnje večjih delt v.
Povečanje delte v, ki jo zagotavlja pogonski sistem, se lahko doseže s:
- stopnjevanjem pogonov
- povečanjem specifičnega sunka
- izboljšanjem razmerja pogonske mase
Mnogokratni manevri
Ker masno razmerje velja za poljubno dano izgorevanje, se pri mnogokratnih manevrih v nizu masna razmerja množijo.
Tako se lahko pokaže, da, če je izpušna hitrost stalna, se lahko delte v seštevajo:
Kadaj sta in masni razmerji manevrov, in pa delti v prvega in drugega manevra:
kjer je in .
To je le enačba Ciolkovskega za vsoto dveh manevrov.
To je uporabno, saj pomeni, da se lahko delte v izračunajo in preprosto dodajo, masno razmerje pa izračuna za celotno plovilo za vso odpravo. Tako je delta v običajno navajana namesto masnih razmerij, ker zahtevajo množenje.
Zaloge delte v


Pri načrtovanju tira se rabi zaloga delte v kot dober pokazatelj koliko pogonskega potisnega goriva bo zanj potrebno. Raba pogonskega potisnega goriva je eksponentna funkcija delte v v soglasju z enačbo Ciolkovskega. Odvisna je tudi od izpušne hitrosti.
Po zakonu o ohranitvi energije ni mogoče določiti zahteve za delto v, če se upošteva le skupna energija plovila v začetni in končni orbiti, ker se pri izpuhu energija izgublja (glej spodaj). Večino plovil se na primer izstreli v orbito z naklonom dovolj blizu zemljepisne širine izstrelišča, da se izkoristi vrtilna hitrost zemeljskega površja. Če je zaradi razlogov odprave treba postaviti plovilo v orbito z različnim naklonom, je potrebna znatna delta v, čeprav sta specifična kinetična in potencialna energija v končni in začetni orbiti enaki.
Kadar raketa rabi potisk v kratkih izbruhih, se lahko drugi viri njenega pospeševanja zanemarijo, velikost spremembe hitrosti enega izbruha pa se lahko preprosto aproksimira z delto v. Skupna potrebna delta v se lahko potem določi s seštevanjem delt v, potrebnih pri posameznih izbruhih, čeprav se med njimi velikost in smer hitrosti spreminja zaradi gravitacije, na primer v eliptičnem tiru.
Za izračun delte v glej Hohmannova prenosna orbita, dvoeliptična prenosna orbita, gravitacijski manever in medplanetarna transportna mreža (ITN). Pomembno je tudi, da velik potisk zmanjšuje gravitacijske izgube.
Delta v je potrebna tudi za ohranjanje satelita v orbiti in se troši v pogonskih manevrih vzdrževanja orbite. Ker se tovor potisnega goriva na večini satelitov ne more dopolniti, lahko količina začetnega tovora na njem dovolj dobro določa njegovo uporabno življenjsko dobo.
Oberthov pojav
Glede na porabo moči se izkaže, da je pri rabi delte v v smeri hitrosti specifična orbitalna energija, dobljena na enoto delte v, enaka trenutni hitrosti. To se imenuje Oberthov pojav. Pri tem plovilo opravi Oberthov manever, kjer pade v gravitacijsko jamo in nato pospeši, ko pri padanju doseže največjo hitrost. Pojav in manever se imenujeta po Hermannu Oberthu, ki ju je leta 1927 prvi opisal.[2]
Satelit v eliptičnem tiru se na primer učinkoviteje potisne pri višji hitrosti (to je na majhni višini) kot pa pri manjši hitrosti (to je pri veliki višini).
Drug primer je, kadar plovilo preletava planet in izgoreva pogonsko gorivo v najbližjem pristopu in ne dlje stran, kar mu da znatno večjo končno hitrost. To velja še posebej kadar je planet velik z močnim gravitacijskim poljem, na primer Jupiter.
Glej tudi gnane manevre.
Graf svinjske zarebrnice
Zaradi relativnih leg planetov, ki se s časom spreminjajo, so za različne datume izstrelitev potrebne različne delte v. Diagram, ki kaže zahtevano delto v v odvisnosti od časa, se včasih imenuje graf svinjske zarebnrnice (angleško porkchop plot). Takšni grafi so uporabni, ker omogočajo izračun izstrelitvenih oken, saj se lahko izstrelitev izvede kadar je odprava znotraj zmožnosti uporabljenega plovila.[3] Nenavadno ime grafa je nastalo v Nasinem Laboratoriju za reaktivni pogon (JPL) sploh zaradi oblike, ki spominja na svinjsko zarebrnico, in predstavlja računalniško generirani konturni graf datuma izstrelitve in značilnosti datuma prihoda poti medplanetarnega poleta za dano možno izstrelitev do planeta.
Delte v v Osončju
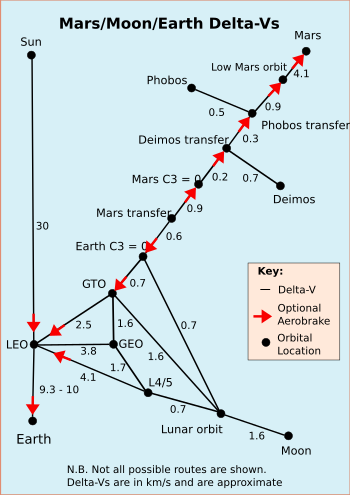
Potrebne delte v za različne orbitalne manevre s konvencionalnimi raketami. Rdeče puščice kažejo kjer se zahtevano izbirno aerozaviranje lahko izvede v tisti določeni smeri, črna števila podajajo delto v v km/s, ki velja v katerikoli smeri.[4][5] Prehodi z nižjimi deltami v se velikokrat lahko pridobijo, vendar zahtevajo redka prenosna okna ali trajajo precej dlje – glej: mehki orbitalni prenosi. Oblika 2.5 za LEO do GTO je večja kot potrebna,[c] oblika 30 za LEO do Sonca je prav tako previsoka.[d]
- C3
- ubežni tir
- GEO
- geosinhrona orbita
- GTO
- geoprenosna orbita
- L4/5
- Lagrangeevi točki L4 in L5 sistema Zemlja–Luna
- LEO
- nizkozemeljska orbita
| Δv [km/s] od (nižje) in k: | LEO (naklon 28°) | LEO (ekvator) | GSO | Lagrangeeva točka L1 | Lagrangeeva točka L2 | Lagrangeevi točki L4 in L5 | Lunina orbita | Lunino površje | ubežna hitrost |
|---|---|---|---|---|---|---|---|---|---|
| zemeljsko površje | 9,3–10.0 | 9,3–10.0 | 13,2–18,2 | 13,9–15,6 | |||||
| LEO 28° | – | 4,24 | 4,33 | 3,77 | 3,43 | 3,97 | 4,04 | 5,93 | 3,22 |
| LEO, ekvator | 4,24 | – | 3,90 | 3,77 | 3,43 | 3,99 | 4,04 | 5,93 | 3,22 |
| GSO | 2,06 | 1,63 | – | 1,38 | 1,47 | 1,71 | 2,05 | 3,92 | 1,30 |
| Lagrangeeva točka L1 | 0,77 | 0,77 | 1,38 | – | 0,14 | 0,33 | 0,64 | 2,52 | 0,14 |
| Lagrangeeva točka L2 | 0,33 | 0,33 | 1,47 | 0,14 | – | 0,34 | 0,64 | 2,52 | 0,14 |
| Lagrangeevi točki L4 in L5 | 0,84 | 0,98 | 1,71 | 0,33 | 0,34 | – | 0,98 | 2,58 | 0,43 |
| nizka Lunina orbita (LLO) | 1,31 | 1,31 | 2,05 | 0,64 | 0,65 | 0,98 | – | 1,87 | 1,40 |
| Lunino površje | 2,74 | 2,74 | 3,92 | 2,52 | 2,53 | 2,58 | 1,87 | – | 2,80 |
| ubežna hitrost za Zemljo | 2,9 | 1,30 | 0,14 | 0,14 | 0,43 | 1,40 | 2,80 | – |
Glej tudi
- zaloga delte v
- gravitacijski upor
- orbitalni manever
- vzdrževanje orbite
- pogon vesoljskega plovila
- specifični sunek
- enačba Ciolkovskega
- delta v (fizika)
- karakteristična energija
Opombe
- ↑ To je lahko na primer za »odpihani« sistem (blow-down system) pri katerem se tlak v rezervoarju zmanjša pri celotni porabi goriva. Poleg velikosti masnega toka goriva se do neke mere zmanjša tudi efektivna hitrost izhajanja izpušnega plina .
- ↑ Potisna sila na enoto mase je , kjer sta in dani funkciji časa .
- ↑ Vsota LEO do GTO in GTO do GEO mora biti enaka LEO do GEO. Točne oblike so odvisne od tega katera nizkozemeljska orbita je uporabljena. Po geoprenosni orbiti (GTO) je hitrost v prizemlju lahko samo 9,8 km/s. To odgovarja LEO na približni višini 700 km, kjer bi bila njena hitrost 7,5 km/s, kar da delto v 2,3 km/s. Če se začne z nižje LEO, to zahteva večjo delto v za GTO, vendar bi morala potem skupna za LEO do GEO biti višja.
- ↑ Hitrost vrtenja Zemlje okrog Sonca je 29,78 km/s, kar ustreza specifični kinetični energiji 443 km2/s2. K temu je treba dodati globino potencialne energije LEO, približno 61 km2/s2, da se dobi kinetična energija blizu Zemlje 504 km2/s2, kar odgovarja hitrosti 31,8 km/s. Ker je hitrost LEO enaka 7,8 km/s, je delta v le 24 km/s. S pomočjo gravitacijskega manevra bi bilo možno doseči Sonce z manjšo delto v. Glej Parker Solar Probe.
Sklici
- ↑ Frozen lunar orbits Arhivirano 2007-02-09 na Wayback Machine.
- ↑ Oberth (1970).
- ↑ »Mars Exploration: Features«. marsprogram.jpl.nasa.gov (v angleščini).
- ↑ »Rockets and Space Transportation« (v angleščini). Arhivirano iz prvotnega spletišča dne 1. julija 2007. Pridobljeno 1. junija 2013.
- ↑ »Delta-V Calculator« (v angleščini). Arhivirano iz spletišča dne 12. marca 2000. Podaja oblike 8.6 od zemeljskega površja do LEO, 4.1 in 3.8 za LEO do Lunine orbite (ali L5) in GEO, 0.7 za L5 do Lunine orbite in 2.2 za Lunino orbito do Luninega površja. Slike izhajajo iz 2. poglavja Space Settlements: A Design Study Arhivirano 2001-11-28 at the Library of Congress na Nasini spletni strani (mrtva povezava).
- ↑ list of delta-v[mrtva povezava]
- ↑ »L2 Halo lunar orbit« (PDF). Arhivirano iz prvotnega spletišča (PDF) dne 25. decembra 2015. Pridobljeno 5. junija 2018.
- ↑ Strategic Considerations for Cislunar Space Infrastructure
Viri
- Oberth, Hermann (1970). »Ways to spaceflight«. Angleški prevod nemškega izvirnika »Wege zur Raumschiffahrt«, (1920). Tunis, Tunizija: Agence Tunisienne de Public-Relations.