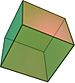
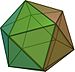
Pravilni politop
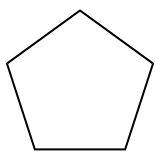 Pravilni petkotnik je mnogokotnik, dvorazsežni politop s 5 robovi, predstavljen s Schläflijevim simbolom {5}. |
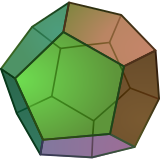 Pravilni dodekaeder je polieder, trirazsežni politop z 12 petkotnimi stranskimi ploskvami, ki so predstavljene s Schläflijevim simbolom {5,3}. |
 Pravilni dodekapleks je polihoron, štirirazsežni politop s 120 dodekaederskimi cellicami, predstavljenimi s Schläflijevim simbolom {5,3,3}. (tukaj je prikazan kot a Schleglov diagram) |
 Pravilno kubično satovje je teselacija, neskončni trirazsežni politop, predstavljen s Schläflijevim simbolom {4,3,4}. |
 256 oglišč in 1024 robov 8-kocke lahko prikažemo v tej ortogonalni projekciji (Petriejev mnogokotnik) | |
Pravilni politop je v matematiki politop, katerega simetrija je prehodna v njegovih zastavah. To daje najvišjo stopnjo simetrije. Vsi njegovi elementi ali j-stranske ploskve (za vse 0 ≤ j ≤ n, kjer je n razsežnost politopa) celice stranske ploskve itd. so tudi prehodni v simetrijah politopa. So pravilni politopi z razsežnostjo ≤ n.
Pravilni politopi so v vseh razsežnostih posplošeni analog pravilnih mnogokotnikov (zgled: kvadrat ali pravilni petkotnik) in pravilnih poliedrov (zgled: kocka).
Razvrstitev in opis
Pravilne politope se razdeli po njihovi razsežnosti.
Lahko se jih še nadalje deli po simetriji. Zgled: pravilni oktaeder ima enako simetrijo kot dodekaeder in ikozaeder. Včasih se grupe simetrije imenujejo po pravilnih politopih. Tako obstajata tetraedrska in ikozaedrska simetrija.
Trije posebni razredi pravilnih politopov obstajajo v vsaki razsežnosti:
- pravilni simpleks
- hiperkocka
- ortopleks
V dveh razsežnostih je neskončno veliko pravilnih mnogokotnikov. V treh in štirih razsežnostih je še več pravilnih poliedrov in polihoronov.
Schläflijevi simboli
Najbolj natančno predstavitev pravilnih politopov je razvil Ludwig Schläfli (1814 – 1895). Malo spremenjena oblika je postala standard. Način označevanja je najlažje razumljiv pri enkratnem dodajanju samo ene razsežnosti.
- konveksni pravilni mnogokotnik, ki ima n stranic, se označuje z {n}. Tako ima enakostraničen trikotnik oznako {3}, kvadrat {4}in tako naprej. Pravilni zvezdni mnogokotnik, ki se ovije m-krat okoli svojega središča, se označuje z {n/m}, kjer sta m in n tuji števili. Pravilni pentagram ima oznako {5/2}.
- pravilni polieder, ki ima {n} stranskih ploskev, ki se združujejo okoli oglišča, označujemo z {n, p}. Devet pravilnih poliedrov je {3, 3} {3, 4} {4, 3} {3, 5} {5, 3} {3, 5/2} {5/2, 3} {5, 5/2} in {5/2, 5}. Pri tem pa je {p} slika oglišč
- pravilni polihoron ali policelica, ki ima {n, p} pri tem pa se q celic združuje okoli roba, se označuje z {n, p, q}. slika oglišča polihorona pa je {p, q}
- petrazsežni pravilni politop se označuje z {n, p, q, r}
- itd.
Dualnost
Dual pravilnega politopa je tudi pravilni politop. Schläflijev simbol dualnega politopa je enak prvotnemu napisanemu v obratnem redu {3, 3} je sebi dualen. {3,4} je dual naslednjim politopom {4,3}, {4,3,3} in {3,3,4}.
Slika oglišč pravilnega politopa je dual politopove facete. Zgled: slika oglišča za {3,3,4} je {3,4}, dual katere je {4,3} to pa je celica za {4,3,3}.
Hiperkocka in križni politop (ortopleks) sta v vseh razsežnostih dualna drug drugemu.
Kadar je Schläflijev simbol palindromski, je polieder sebi dualen. Sebi dualni pravilni politopi so:
- vsi pravilni mnogokotniki {a}
- pravilni n-simpleksi {3, 3, …, 3}
- pravilna 24-celica v štirih razsežnostih {3, 4, 3}
- vsa pravilna n-razsežna satovja {4, 3, ….3, 4}. Obravnavamo jih lahko kot neskončne politope.
Pravilni simpleksi

|

|

|

|
| daljica | trikotnik | tetraeder | pentahoron |

|

|

|
Najprej se označi točko A. Nato še točko B na razdalji r od nje. Poveže se ju tako, da se dobi daljico. Označi se točko C na pravokotni razdalji r od obeh. Povežeta se A in B, da se dobi enakostranični trikotnik. Označi se točko D v tretji pravokotni razsežnosti na razdalji r od vseh treh. Poveže se vse v pravilni tetraeder. Tako se lahko nadaljuje v višje razsežnosti.
To so pravilni simpleksi, ki jih imenujemo na naslednji način:
- točka
- daljica
- enakostranični trikotnik
- pravilni tetraeder
- pravilni pentahoron ali 4-simpleks
- pravilni heksateron ali 5-simpleks
… n-simpleks ima n+1 oglišč.
Hiperkocke

|
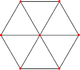
|

|
| kvadrat | kocka | teserakt |

|

|

|
Pričnimo s točko A. Podaljšajmo premico do točke B na razdalji r. Povežimo tako, da dobimo daljico. Podaljšajmo drugo daljico na dolžino r pravokotno na AB od B do C. Podobno naredimo od A do D, da dobimo kvadrat ABCD. Podaljšamo daljice z dolžino r iz vsakega kota pravokotno na AB in BC. Označimo nove točke z E, F, G in H. Tako dobimo kocko ABCDEFGH. Podobno lahko naredimo za višje razsežnosti. Kar smo dobili so hiperkocke ali merilni politopi. Njihova imena so v zaporedju razsežnosti:
- točka
- daljica
- kvadrat (pravilni tetragon)
- kocka (pravilni heksaeder)
- teserakt (pravilni oktahoron) ali 4-kocka
- penterakt (pravilni dekateron) ali 5-kocka
- ....n-kocka ima 2n oglišč
Ortopleksi

|

|

|
| kvadrat | oktaeder | 16-celica |

|

|

|
Pričnimo s točko O in razširimo premico v nasprotno smer do točk A in B, ki sta na razdalji r od O in na medsebojni razdalji 2r. Narišimo premico COD z dolžino 2r s središčem v O in pravokotno na AB. Povežimo konce kvadrata ABCD. Narišimo premico EOF z enako dolžino s središčem v O pravokotno na AB in CD. Povežimo konce v kvadrat, da dobimo pravilni oktaeder. Podobno naredimo za višje razsežnosti.
To so ortopleksi ali križni politopi. Njihova imena v zaporedju razsežnosti so
- točka
- daljica
- kvadrat
- pravilni oktaeder
- pravilni heksadekakron (16-celica) ali 4-ortopleks
- pravilni triakontakaiditeron (pentakros) ali 5-ortopleks
- ...n-ortopleks ima 2n oglišč
Odkrivanje
Konveksni mnogokotniki in poliedri
Prve obdelave pravilnih mnogokotnikov izvirajo iz antične Grčije. Znana so jim že bila platonska telesa
Zvezdni mnogokotniki in poliedri
Razumevanje zvezdnih mnogokotnikov in poliedrov je po Evklidu ostalo enako še mnogo stoletij. Prvi, ki je resno proučeval mnogokotnike je bil Thomas Bradwardine (1290 -1349). Različni zvezdni poliedri so se pojavili v renesančni umetnosti. Johannes Kepler (1571 – 1630) je proučeval mali stelirani dodekaeder in veliki stelirani dodekaeder in zanju ugotovil, da sta pravilna. Louis Poinsot (1777 – 1859) je odkril veliki dodekaeder in veliki ikozaeder v letu 1809. Augustin Louis Cauchy (1789 - 1857) je podal popolni seznam v letu 1812. Ti poliedri so dandanes poznani kot Kepler-Poinsotovi poliedri.
ApeirotopiKepler-Poinsotovi poliedri 



mali stelirani
dodekaederveliki stelirani
dodekaederveliki dodekaeder veliki ikozaeder
Politopi v višjih razsežnostih

Šele v 19.stoletju je Ludwig Schläfli (1814 -1895) proučeval pravilne politope v višjih razsežnostih. Njegovo delo je bilo objavljeno šele šest let po smrti.
Coxeter je v letu 1948 v svojem delu obdelal Schläflijeve ugotovitve. Schläfli obstaja šest pravilnih konveksnih politopov v 4 razsežnostih. Njihovi odnosi do platonskih teles je naslednji: 4 simpleks (pentahoron), 120-celica in 600-celica po vrsti odgovarjajo tetraedru, dodekaedru in ikozaedru. Hiperkocka ali teserakt, 24-celica in heksaeder (ali 4-ortopleks ali 16-celica) po vrsti odgovarjajo kocki, hibridu kocka/oktaeder in oktaedru.
V petih in več razsežnostih so natančno trije pravilni politopi, ki odgovarjajo tetraedru, kocki in oktaedru. To so pravilni simpleks, hiperkocka in ortopleks.
Proti koncu 19. stoletja sta matematika Arthur Cayley (1821 – 1895) in Ludvig Schläfli (1814 – 1895) razvila teorijo o pravilnih politopih v štirih in višjih razsežnostih. Takšni so teserakt in 24-celica.
Zadnjega si je zelo težko predstavljati. Teserakt vsebuje osem kubičnih celic, ki so sestavljene iz dveh kock v vzporednih hiperravninah s pripadajočimi oglišči navzkrižno povezanimi tako, da je osem križnih robov enakih po dolžini in pravokotnih na 12 +12 robov, ki ležijo na vsaki kocki. Pripadajoče stranske ploskve so povezane tako, da tvorijo ostalih šest kubičnih stranskih ploskev teserakta. 24-celica se lahko dobi iz teserakta s povezovanjem osmih oglišč vsake od kubičnih stranskih ploskev v dodatno oglišče. To tvori štirirazsežno analogijo piramide. Obe obliki in ostale štirirazsežne oblike si lahko neposredno predstavljamo z uporabo štirirazsežnega stereografa.
Še težje si je predstavljati ostale abstraktne pravilne politope kot sta 57-celica ali 11-celica.
V začetku 20. stoletja je bila definicija pravilnega politopa naslednja:
- pravilni mnogokotnik je tisti mnogokotnik, ki ima robove in kote enake.
- pravilni polieder je polieder katerega stranske ploskve so skladni pravilni mnogokotniki in njihove slike oglišč so skladne in pravilne
- in tako dalje: n-politop je n-razsežni politop, katerega n-1 razsežne stranske ploskve so pravilne in skladne, njihove slike oglišč pa so pravilne in skladne.
Ta definicija je rekurzivna, ker določa pravilnost oblik višjih razsežnosti s pomočjo pravilnosti oblik nižje razsežnosti. Razen te, obstaja še nerekurzivna definicija, ki trdi, da je politop pravilen, če ima dovolj veliko stopnjo simetrije.
- n-politop je pravilen, če vsaka množica, ki jo sestavlja oglišče, vsebuje tudi rob. Dvorazsežna stranska ploskev vsebuje rob. Tako lahko nadaljujemo vse do n-1 razsežnosti.
Zgled:kocka je pravilno telo, ker takrat, ko izberemo oglišče kocke in eno izmed treh robov, ki prihajajo vanj ter eno izmed dveh stranskih ploskev, ki vsebujejo rob. V tem primeru trojico ali zastavo (oglišče, rob, stranska ploskev) lahko preslikamo v poljubno zastavo s pomočjo primerne simetrije kocke. Tako lahko definiramo pravilni politop na naslednji način:
- pravilni politop je tisti, ki je prehoden na svojih zastavah.
Aperotopi - neskončni politopi
V prvem delu 20. stoletja sta Coxeter in Petrie odkrila tri neskončne strukture {4, 6}, {6, 4} in {6, 6}. imenovala sta jih poševni poliedri, ker sta mislila, da zadoščajo definiciji pravilnega poliedra: vsa oglišča, robovi in stranske ploskve so si podobne, vsi koti so enaki in telo nima prostih robov. Danes jih imenujemo neskončni poliedri ali apeiroedri. Pravilna tlakovanja na ravnini {4,4}, {3,6} in {6,3} se tudi obravnavajo kot neskončni poliedri.
Pravilni kompleksni politopi
Kompleksno število ima realni del in imaginarni del, ki je mnogokratnik kvadratnega korena iz minus ena. Kompleksni Hilbertov prostor ima svoje koordinate x, y, z itd. kot kompleksna števila. To v resnici podvoji število razsežnosti. Politop, ki ga konstruiramo v takšnem unitarnem prostoru, se imenuje kompleksni politop.
Abstraktni politopi
Grünbaum je odkril tudi 11-celico. To je štirirazsežni objekt, katerega facete niso ikozaedri ampak so "hemiikozaedri". To so oblike, ki jih dobimo tako, da vzamemo nasprotne stranske ploskve ikozaedra kot da so v resnici iste stranske ploskve. Hemiikozaeder ima samo 10 trikotnih stranskih ploskev in 6 oglišč. Ikozaeder pa ima 20 stranskih ploskev in 12 oglišč.
Konstrukcije
Mnogokotniki
Običajni način konstruiranja pravilnega mnogokotnika v ravnini je konstrukcija z ravnilom in šestilom. Risanje nekaterih pravilnih mnogokotnikov je zelo preprosto. Nekaterih pa ne moremo narisati. Najenostavnejši n-stranski pravilni mnogokotniki, ki jih ni mogoče narisati so tisti, ki imajo število stranic n enako: 7, 9,11, 13, 14, 18, 19, 21, ….
Poliedri
Evklidova knjiga Elementi nudi večje število konstrukcij z ravnilom in šestilom za platonska telesa (glej http://www.dform.com/projects/euclid/home.html Arhivirano 2007-10-28 na Wayback Machine. Evklidovi elementi).
Beseda konstruirati je povezana s sistematično izgradnjo stvari. Najbolj pogost način za konstrukcijo pravilnega poliedra je razvoj mreže. Da dobimo z razvojem mreže polieder, moramo vzeti površino poliedra in jo odrezati vzdolž robov tako, da lahko površino izravnamo v ravnino. To nam da ravnino neraztegnjenega poliedra. Ker pa imajo platonska telesa za stranske ploskve samo trikotnike, kvadrate in petkotnike. Te like lahko konstruiramo z ravnilom in šestilom. Tako obstajajo tudi načini za risanje teh mrež. To se lahko uporabi tudi za zvezdne poliedre, čeprav moramo biti previdni pri izdelavi mreže za poliedre , ki jim vidimo samo zunanjo površino.
Višje razsežnosti



V višjih razsežnostih postaja vse težje razumeti, kaj pomeni izraz konstruirati neki objekt. V trirazsežnem prostoru je nemogoče ustvariti fizični model objekta, ki ima 4 ali več razsežnosti. Obstaja nekaj načinov, s pomočjo katerih se ta problem rešuje.
Prvi način je primeren za štiri razsežnosti in uporablja štirirazsežno stereografijo.
Drugi način je potopitev objekta z višjo razsežnostjo v trirazsežni prostor. Pri tem pa se uporabljajo načini analogni načinom prikazovanja trirazsežnih teles v ravnini. Tako na primer imajo razvite mreže višje razsežni ekvivalent. Nekaj teh lahko pogledamo na strani [1] Arhivirano 2011-07-17 na Wayback Machine.. Lahko si predstavljamo izgradnjo modela iz teh mrež, če bi narisali mrežo poliedra na papir. Žal nikoli ne moremo opraviti potrebnih upogibanj trirazsežne strukture, da bi dobili štirirazsežni politop ali polihoron zaradi fizičnih omejitev prostora. Naslednji način za risanje večrazsežnih oblik v treh razsežnostih je vrsta projekcije. Zgled: ortografska projekcija ali perspektivna projekcija. (glej [2]). Celo potopitev štirirazsežnega polihorona v dve razsežnosti je lahko problematična. Lažje razumljivi so modeli trirazsežnih projekcij.
Drugi način, ki je razumljiv opazovalcu v trirazsežnem prostoru, je v tem, da štirirazsežni polihoron potopimo v objekt s pomočjo tehnologije navidezne resničnosti. Zgled: predstavljajmo si, da nekdo hoče vedeti, če je prostor napolnjen s kockami. Opazovalec bo sedel znotraj ene kocke in bo lahko videl kocke pred seboj, za seboj zgoraj in spodaj ter levo in desno. Če bi potoval v teh smereh, bi lahko raziskoval vrste kock in tako razumel strukturo prostora. Res, da neskončna vrsta kock ni politop. V resnici je to teselacija trirazsežnega prostora. Seveda štirirazsežni polihoron se lahko obravnava kot teselacija trirazsežnega neevklidskega prostora oziroma teselacija površine štirirazsežne sfere (štirirazsežno sferno tlakovanje).
Glej tudi
Zunanje povezave
- Pravilni politop na Glossary for Hyperspace (angleško)
- Navigator po poliedrih (Stella) (angleško)
- Umetniške oblike v naravi Arhivirano 2012-07-04 na Wayback Machine. (nemško)
- Slike poliedrov (angleško)
- Mreže poliedrov (angleško)