Комутативни прстен
У теорији прстена, грани апстрактне алгебре, комутативни прстен је прстен у коме је операција множења комутативна. Ово значи да ако су a и b било која два елемента прстена, онда је a×b=b×a.
Проучавање комутативних прстена се назива комутативна алгебра.
Дефиниција и први примери
Дефиниција
Прстен је скуп опремљен са две бинарне операције, тј. операцијама које комбинују било која два елемента прстена у трећи. Зову се сабирање и множење и обично се означавају са „” и „”; на пример и . Да би се формирао прстен, ове две операције морају да задовоље бројна својства: прстен мора бити абелова група под сабирањем, као и моноид под множењем, где се множење дистрибуира преко сабирања; тј. . Елементи идентитета за сабирање и множење су означени са и .
Ако је множење комутативно, тј. тада се прстен назива комутативним. У остатку овог чланка, сви прстенови ће бити комутативни, осим ако је експлицитно другачије наведено.
Први примери
Важан пример, и у неком смислу кључан, је прстен целих бројева са две операције сабирања и множења. Пошто је множење целих бројева комутативна операција, ово је комутативни прстен. Обично се означава са као скраћеница од немачке речи Zahlen (бројеви).
Поље је комутативни прстен где је и сваки елемент који није нула је инверзибилан; тј. има мултипликативну инверзну вредност такву да је . Према томе, по дефиницији, било које поље је комутативни прстен. Рационални, реални и комплексни бројеви формирају поља.
Ако је дати комутативни прстен, онда скуп свих полинома у променљивој чији су коефицијенти у формира полиномски прстен, означен као . Исто важи и за неколико променљивих.
Ако је неки тополошки простор, на пример подскуп неког, континуалне функције реалне- или комплексне вредности на формирају комутативни прстен. Исто важи и за диференцијабилне или холоморфне функције, када су два концепта дефинисана, као што је комплексна многострукост.
Дељивост
За разлику од поља, где је сваки елемент различит од нуле мултипликативно инвертибилан, концепт дељивости за прстенове је богатији. Елемент прстена назива се јединица ако поседује мултипликативну инверзну вредност. Други посебан тип елемента су делиоци нуле, односно елемент прстена такав да постоји елемент прстена који није нула, при чему је . Ако не поседује делиоце нуле који нису нула, назива се интегрални домен (или домен). Елемент који задовољава за неки позитиван цео број се назива нилпотентним.
Локализације
Локализација прстена је процес у коме се неки елементи претварају у инвертибилне, тј. у прстену се додају мултипликативни инверзи. Конкретно, ако је мултипликативно затворен подскуп од (тј. кад год онда је и ) онда је локализација на , или прстен разломака са имениоцима у , који се обично означава састављен од симбола
подлежу одређеним правилима која опонашају поништавање познато из рационалних бројева. Заиста, на овом језику је локализација различита од нуле за све целе бројеве. Ова конструкција функционише за било који интегрални домен уместо . Локализација је поље које се назива количник поља .
Примери
- Најважнији пример је прстен целих бројева са операцијама сабирања и множења. Уобичајено множење целих бројева је комутативно. Прстен се обично обележава словом Z, од немачке речи Zahlen (бројеви).
- Рационални, реални и комплексни бројеви чине комутативне прстене; они су штавише поља.
- Општије, свако поље је комутативни прстен, па је класа поља поткласа класе комутативних прстенова.
- Прост пример некомутативног прстена је скуп свих матрица димензије 2-са-2 чији су елементи реални бројеви. На пример, множење матрица
- није једнако множењу изведеном супротним редоследом:
- Ако је n позитиван цео број, тада скуп Zn целих бројева по модулу n чини комутативни прстен са n елемената (види модуларна аритметика).
- Ако је R дати комутативни прстен, онда је скуп свих полинома променљиве X чији коефицијенти су из R гради нови комутативни прстен који се означава са R[X].
Локални прстени
прстен се назива локалним ако има само један максимални идеал, означен са m. За било који (не нужно локални) прстен R, локализација
на простом идеалу p је локалнa. Ова локализација одражава геометријска својства Спец R „око p”. Неколико појмова и проблема у комутативној алгебри могу се свести на случај када је R локално, што локалне прстенове чини посебно дубоко проучаваном класом прстенова. Поље остатка R је дефинисано као
Било који R-модул M даје k-векторски простор дат са M / mM. Накајамина лема показује да овај пасус чува важне информације: коначно генерисани модул M је нула ако и само ако је M / mM нула.
Редовни локални прстенови
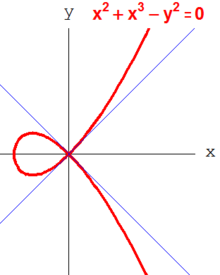
k-векторски простор m/m2 је алгебарска инкарнација котангенсног простора. Неформално, елементи од m се могу сматрати функцијама које нестају у тачки p, док m2 садржи оне које нестају редоследом од најмање 2. За било који Нетеров локални прстен R, неједнакост
важи, одражавајући идеју да котангентни (или еквивалентно тангентни) простор има најмање димензију простора Спец R. Ако је једнакост истинита у овој процени, R се назива регуларним локалним прстеном. Нетеров локални прстен је правилан ако и само ако је прстен (који је прстен функција на тангентном конусу) изоморфан полиномском прстену над k. Уопштено говорећи, регуларни локални прстенови су донекле слични полиномским прстеновима.[1] Уобичајени локални прстенови су УФД-ови.[2]
Дискретни прстенови за вредновање су опремљени функцијом која додељује цео број било ком елементу r. Овај број, назван вредновање r, може се неформално сматрати нултим или полним редом r. Дискретни вредносни прстенови су управо једнодимензионални регуларни локални прстенови. На пример, прстен клица холоморфних функција на Римановој површини је дискретни вредносни прстен.
Комплетни пресеци

По Круловој главној теореми идеала, темељном резултату теорије димензија прстенова, димензија
је најмање r − n. Прстен R се назива комплетним пресечним прстеном ако се може представити на начин који постиже ову минималну границу. Овај појам се такође углавном проучава за локалне прстенове. Сваки регуларни локални прстен је комплетан пресечни прстен, али не и обрнуто.
Прстен R је потпуни пресек у теорији скупова ако је редуковани прстен придружен R, тј. онај добијен дељењем свих нилпотентних елемената, потпуни пресек. Према подацима из 2017. године, генерално је непознато да ли су криве у тродимензионалном простору потпуни пресеци теоријских скупова.[3]
Коен-Маколејеви прстенови
Дубина локалног прстена R је број елемената у неком (или, како се може показати, било ком) максималном регуларном низу, тј. низу a1, ..., an ∈ m тако да су сви ai делиоци различити од нуле у
За било који локални Нетеров прстен, важи неједнакост
Локални прстен у коме се остварује једнакост назива се Коен–Маколејев прстен. Локални комплетни пресечни прстенови, и а фортиори, регуларни локални прстенови су Коен–Маколеј, али не и обрнуто. Кохен–Макалеј комбинује пожељна својства регуларних прстенова (као што је особина да буду универзални ланчани прстенови, што значи да се (ко)димензија простих бројева добро понаша), али су такође робустнији у узимању количника од регуларних локалних прстенова.[4]
Референце
- ^ Matsumura (1989, стр. 143, §7, Remarks) harv грешка: више циљева (2×): CITEREFMatsumura1989 (help)
- ^ Matsumura (1989, §19, Theorem 48) harv грешка: више циљева (2×): CITEREFMatsumura1989 (help)
- ^ Lyubeznik (1989)
- ^ Eisenbud (1995, Corollary 18.10, Proposition 18.13) harv грешка: више циљева (3×): CITEREFEisenbud1995 (help)
Литература
- Christensen, Lars Winther; Striuli, Janet; Veliche, Oana (2010), „Growth in the minimal injective resolution of a local ring”, Journal of the London Mathematical Society, Second Series, 81 (1): 24—44, S2CID 14764965, arXiv:0812.4672
 , doi:10.1112/jlms/jdp058
, doi:10.1112/jlms/jdp058 - Eisenbud, David (1995), Commutative algebra. With a view toward algebraic geometry., Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94268-1, MR 1322960
- Hochster, Melvin (2007), „Homological conjectures, old and new”, Illinois J. Math., 51 (1): 151—169, doi:10.1215/ijm/1258735330

- Jacobson, Nathan (1945), „Structure theory of algebraic algebras of bounded degree”, Annals of Mathematics, 46 (4): 695—707, ISSN 0003-486X, JSTOR 1969205, doi:10.2307/1969205
- Lyubeznik, Gennady (1989), „A survey of problems and results on the number of defining equations”, Representations, resolutions and intertwining numbers, стр. 375—390, Zbl 0753.14001
- Matsumura, Hideyuki (1989), Commutative Ring Theory, Cambridge Studies in Advanced Mathematics (2nd изд.), Cambridge University Press, ISBN 978-0-521-36764-6
- Pinter-Lucke, James (2007), „Commutativity conditions for rings: 1950–2005”, Expositiones Mathematicae, 25 (2): 165—174, ISSN 0723-0869, doi:10.1016/j.exmath.2006.07.001

- Atiyah, Michael; Macdonald, I. G. (1969), Introduction to commutative algebra, Addison-Wesley Publishing Co.
- Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Commutative Noetherian and Krull rings, Ellis Horwood Series: Mathematics and its Applications, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155615-7
- Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Dimension, multiplicity and homological methods, Ellis Horwood Series: Mathematics and its Applications., Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155623-2
- Kaplansky, Irving (1974), Commutative rings (Revised изд.), University of Chicago Press, MR 0345945
- Nagata, Masayoshi (1975) [1962], Local rings, Interscience Tracts in Pure and Applied Mathematics, 13, Interscience Publishers, стр. xiii+234, ISBN 978-0-88275-228-0, MR 0155856
- Zariski, Oscar; Samuel, Pierre (1958), Commutative Algebra I, II, University series in Higher Mathematics, Princeton, N.J.: D. van Nostrand, Inc. (Reprinted 1975-76 by Springer as volumes 28-29 of Graduate Texts in Mathematics.)
- Artin, Michael (2018). Algebra (2nd изд.). Pearson.
- Atiyah, Michael; Macdonald, Ian G. (1969). Introduction to commutative algebra. Addison–Wesley.
- Bourbaki, N. (1964). Algèbre commutative. Hermann.
- Bourbaki, N. (1989). Algebra I, Chapters 1–3. Springer.
- Cohn, Paul Moritz (2003), Basic algebra: groups, rings, and fields, Springer, ISBN 978-1-85233-587-8.
- Eisenbud, David (1995). Commutative algebra with a view toward algebraic geometry. Springer.
- Gallian, Joseph A. (2006). Contemporary Abstract Algebra, Sixth Edition. Houghton Mifflin. ISBN 9780618514717.
- Gardner, J.W.; Wiegandt, R. (2003). Radical Theory of Rings. Chapman & Hall/CRC Pure and Applied Mathematics. ISBN 0824750330.
- Herstein, I. N. (1994) [reprint of the 1968 original]. Noncommutative rings. Carus Mathematical Monographs. 15. With an afterword by Lance W. Small. Mathematical Association of America. ISBN 0-88385-015-X.
- Hungerford, Thomas W. (1997). Abstract Algebra: an Introduction, Second Edition. Brooks/Cole. ISBN 9780030105593.
- Jacobson, Nathan (2009). Basic algebra. 1 (2nd изд.). Dover. ISBN 978-0-486-47189-1.
- Jacobson, Nathan (1964). „Structure of rings”. American Mathematical Society Colloquium Publications (Revised изд.). 37.
- Jacobson, Nathan (1943). „The Theory of Rings”. American Mathematical Society Mathematical Surveys. I.
- Kaplansky, Irving (1974), Commutative rings (Revised изд.), University of Chicago Press, ISBN 0-226-42454-5, MR 0345945.
- Lam, Tsit Yuen (2001). A first course in noncommutative rings. Graduate Texts in Mathematics. 131 (2nd изд.). Springer. ISBN 0-387-95183-0.
- Lam, Tsit Yuen (2003). Exercises in classical ring theory. Problem Books in Mathematics (2nd изд.). Springer. ISBN 0-387-00500-5.
- Lam, Tsit Yuen (1999). Lectures on modules and rings. Graduate Texts in Mathematics. 189. Springer. ISBN 0-387-98428-3.
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third изд.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556, Zbl 0984.00001.
- Matsumura, Hideyuki (1989). Commutative Ring Theory. Cambridge Studies in Advanced Mathematics (2nd изд.). Cambridge University Press. ISBN 978-0-521-36764-6.
- Milne, J. „A primer of commutative algebra”.
- Rotman, Joseph (1998), Galois Theory (2nd изд.), Springer, ISBN 0-387-98541-7.
- van der Waerden, Bartel Leendert (1930), Moderne Algebra. Teil I, Die Grundlehren der mathematischen Wissenschaften, 33, Springer, ISBN 978-3-540-56799-8, MR 0009016.
- Warner, Seth (1965). Modern Algebra. Dover. ISBN 9780486663418.
- Wilder, Raymond Louis (1965). Introduction to Foundations of Mathematics. Wiley.
- Zariski, Oscar; Samuel, Pierre (1958). Commutative Algebra. 1. Van Nostrand.
- Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Commutative Noetherian and Krull rings, Mathematics and its Applications, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155615-7
- Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Dimension, multiplicity and homological methods, Mathematics and its Applications, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155623-2
- Ballieu, R. (1947). „Anneaux finis; systèmes hypercomplexes de rang trois sur un corps commutatif”. Ann. Soc. Sci. Bruxelles. I (61): 222—227.
- Berrick, A. J.; Keating, M. E. (2000). An Introduction to Rings and Modules with K-Theory in View. Cambridge University Press.
- Cohn, Paul Moritz (1995), Skew Fields: Theory of General Division Rings
 , Encyclopedia of Mathematics and its Applications, 57, Cambridge University Press, ISBN 9780521432177
, Encyclopedia of Mathematics and its Applications, 57, Cambridge University Press, ISBN 9780521432177 - Eisenbud, David (1995), Commutative algebra. With a view toward algebraic geometry., Graduate Texts in Mathematics, 150, Springer, ISBN 978-0-387-94268-1, MR 1322960
- Gilmer, R.; Mott, J. (1973). „Associative Rings of Order”. Proc. Japan Acad. 49: 795—799. doi:10.3792/pja/1195519146
 .
. - Harris, J. W.; Stocker, H. (1998). Handbook of Mathematics and Computational Science. Springer.
- Isaacs, I. M. (1994). Algebra: A Graduate Course. AMS. ISBN 978-0-8218-4799-2.
- Jacobson, Nathan (1945), „Structure theory of algebraic algebras of bounded degree”, Annals of Mathematics, Annals of Mathematics, 46 (4): 695—707, ISSN 0003-486X, JSTOR 1969205, doi:10.2307/1969205
- Knuth, D. E. (1998). The Art of Computer Programming. 2: Seminumerical Algorithms (3rd изд.). Addison–Wesley.
- Korn, G. A.; Korn, T. M. (2000). Mathematical Handbook for Scientists and Engineers. Dover. ISBN 9780486411477.
- Milne, J. „Class field theory”.
- Nagata, Masayoshi (1962) [1975 reprint], Local rings, Interscience Tracts in Pure and Applied Mathematics, 13, Interscience Publishers, ISBN 978-0-88275-228-0, MR 0155856
- Pierce, Richard S. (1982). Associative algebras. Graduate Texts in Mathematics. 88. Springer. ISBN 0-387-90693-2.
- Poonen, Bjorn (2018), Why all rings should have a 1 (PDF), arXiv:1404.0135

- Serre, Jean-Pierre (1979), Local fields, Graduate Texts in Mathematics, 67, Springer
- Springer, Tonny A. (1977), Invariant theory, Lecture Notes in Mathematics, 585, Springer, ISBN 9783540373704
- Weibel, Charles. „The K-book: An introduction to algebraic K-theory”.
- Zariski, Oscar; Samuel, Pierre (1975). Commutative algebra. Graduate Texts in Mathematics. 28–29. Springer. ISBN 0-387-90089-6.
- Fraenkel, A. (1915). „Über die Teiler der Null und die Zerlegung von Ringen”. J. Reine Angew. Math. 145: 139—176.
- Hilbert, David (1897). „Die Theorie der algebraischen Zahlkörper”. Jahresbericht der Deutschen Mathematiker-Vereinigung. 4.
- Noether, Emmy (1921). „Idealtheorie in Ringbereichen”. Math. Annalen. 83 (1–2): 24—66. S2CID 121594471. doi:10.1007/bf01464225.
Спољашње везе
![]() Медији везани за чланак Комутативни прстен на Викимедијиној остави
Медији везани за чланак Комутативни прстен на Викимедијиној остави















![{\displaystyle R\left[X\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73de3a1ad1ac968cfce515ecb04c96a8633f60bf)















