Rotacija stabla

U diskretnoj matematici, rotacija stabla je operacija na binarnom stablu koja menja strukturu ali ne i redosled elemenata. Rotacija stabla pomera jedan čvor kao gore u stablu, a jedan ka dole. Koristi se da bi se stablu promenio oblik, tj. konkretno visina, pomeranjem manjih podstabala dole a većih gore, što rezultuje većom efikasnošću kod mnogih operacija sa stablima.
Ne postoji konzistentnost kod različitih definicija smera rotacija. Neki kažu da smer rotacije zavisi od strane ka kojoj su čvorovi pomereni, dok drugi kažu da zavisi od toga koje dete zauzima mesto korena (suprotno od prošlog). Ovaj članak prihvata pristup da smer zavisi od strane na koju se pomera.
Ilustracija
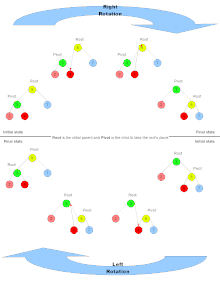
Operacija desne rotacije, kao što je prikazano na slici iznad, izvršena je za koren Q stoga je to desna rotacija u čvoru Q. Ova operacija rezultuje rotacijom stabla u smeru kazaljke na satu. Obrnuta operacija je leva rotacija, koja rezultuje rotacijom u smeru suprotnom od smera kazaljke na satu (prikazana leva rotacija je u čvoru P). Ključ shvatanja kako rotacija funkcioniše je shvatanje njenih ograničena. Na primer redosled čvorova stabla (kada se čina sa leva na desno npr.) ne može da se promeni (drugi način da se to sagleda je da redosled kojim su čvorovi posećeni u inorder obilasku mora da bude isti pre i posle operacije). Još jedno ograničenje je glavna odlika binarnog stabla pretrage, da je desno dete veće od roditelja a levo manje. Primetimo da desno dete levog deteta korena podstabla (npr. čvor B u dijagramu za stablo sa korenom u Q) može da postane levo dete korena, koje ujedino postaje desno dete "novog" korena u rotiranom podstablu, bez kršenja ijednog od ograničenja. Kao što možete primetiti iz dijagrama, redosled čvorova se ne menja. Suprotna operacija takodje čuva redosled i predstavlja drugu vrstu rotacije.
Pod pretpostavkom da je ovo binaro stablo pretrage, kao što je navedeno iznad, elementi moraju da se protumače kao konkretne vrednosti koje mogu međusobno da se porede. slova iznad koriste se kao kontejneri za ove vrednosti.
Detaljna ilustracija
Kada je podstablo rotirano, visina strane na koju je primenjena rotacija povećava se za 1, dok se visina suprotne strane smanjuje za 1. Zbog ove činjenice rotacije su korisne za rebalansiranje stabla.
Koristi se terminologija Koren za roditelja podstabla koje se rotira, Pivot za čvor koji će postati novi roditelj, SR za stranu na koju je rotacija primenjena i SS za suprotnu stranu. U dijagramu iznad za čvor Q, SR je C a SS je P. Pseudo kod za rotaciju je:
Pivot = Koren.SS Koren.SS = Pivot.SR Pivot.SR = Koren Koren = Pivot
Ovo je operacija konstantnog vremena izvršavanja.
Programer mora da se postara da roditelj korena pokazuje na pivot posle rotacije. Takodje, programer mora da zna da ova operacija može da promeni glavni koren stabla i da shodno tome promeni pokazivače.
Inorder Invarijanta
Rotacija stvara inorder obilazak invarijante binarnog stabla. Ovo podrazumeva da redosled elemenata nije promenjen kada je rotacija primenjena u bilo kom delu stabla. Inorder obilazak stabala koja su prikazana gore:
Levo stablo: ((A, P, B), Q, C) Desno stablo: (A, P, (B, Q, C))
Pravljenje jednog iz drugog je jednostavno. Ono što sledi je primer Python koda koji obavlja to izračunavanje:
def desna_rotacija(koren):
levo, Q, C = koren
A, P, B = levo
return (A, P, (B, Q, C))
Još jedan način gledanja na ovo je:
Desna rotacija čvora Q:
Neka je P levo dete od Q. Namesti da levo dete od Q bude desno dete od P. Nameti da desno dete od P bude Q.
Leva rotacija čvora P:
Neka je Q desno dete od P. Namesti da desno dete od P bude levo dete od Q. Namesi da levo dete od Q bude P.
Ostale grane su ostale iste.
Takođe postoje i duple rotacije koje su kombinacije leve i desne rotacije. Dupla leva rotacija u X može biti definisana kao desna rotacija desnog deteta od X praćena levom rotacijom X; slično, dupla desna rotacija u X može biti definisana kao leva rotacija levog detete od X praćena desnom rotacijom X.
Rotacija stabla koristi se u mnogim strukturama podataka, kao što su AVL stabla, crveno-crna stabla, splay stabla, i treap stabla. Zahtevaju konstantno vreme pošto su lokalne transformacije: operišu samo na 5 čvorova, i ne moraju da obilaze ostatak stabla.
Rebalansiranje pomoću rotacija

Stablo može biti rebalansirano pomoću rotacija. Posle rotacije, visina strane na koju je primenjena rotacija povećava se za 1, dok se visina druge strane smanjuje za 1. Stoga, rotacije mogu biti strateški primenjene na čvorove kojima je razlika visina levog i desnog deteta veća od 1. Samo-balansirajuća binarna stabla primenjuju ovu operaciju automatski. Tip stabla koje koristi ovu tehniku rebalansiranja je AVL stablo.
Razdaljina rotacije
Razdaljina rotacije između dva binarna stabla sa istim brojem čvorova je minimalan broj rotacija potreban da se jedno stablo pretvori u drugo. Sa ovom razdaljinom, niz stabala sa n čvorova postaje metrički prostor: razdaljina je simetrična, pozitivna za dva različita stabla, i zadovoljava nejednakost trouglova.
Problem da li postoji algoritam polinomijalne složenosti koji računa razdaljinu rotacije i dalje je otvoren.
Daniel Sleator, Robert Tarjan i William Thurston pokazali su da je razdaljina rotacije između dva stabla sa n čvorova (za n ? 11) najviše 2n − 6, i da je beskonačno mnogo parova stabala na ovoj razdaljini.[1]
Vidi još
- AVL stabla, crveno-crna stabla, i splay stabla, vrste binarnog stabla pretrage strukture podataka koja koristi rotacije da održi balans stabla.
- Associativity of a binary operation means that performing a tree rotation on it does not change the final result.
- Day–Stout–Warren algoritam balansira neizbalansirano binarno stablo pretrage.
- Tamari lattice, posebno uređen set u kome elementi mogu biti definisani kao binarna stabla a redosled elemenata definisan je rotacijama.
Reference
- ^ Sleator, Daniel D.; Tarjan, Robert E.; Thurston, William P. (1988), „Rotation distance, triangulations, and hyperbolic geometry”, Journal of the American Mathematical Society, American Mathematical Society, 1 (3): 647—681, JSTOR 1990951, MR 928904, doi:10.2307/1990951.
Spoljašnje veze
- Java appleti koji demonstriraju rotaciju stabla
- Rotacija AVL stabla - tutorial Архивирано на сајту Wayback Machine (6. фебруар 2012) (RTF) by John Hargrove
