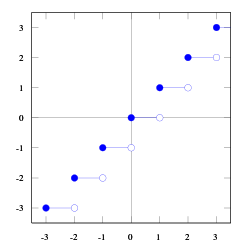
Golv-_och_takfunktionerna

Golv- och takfunktionerna är två funktioner inom talteorin.

Värdet av golvfunktionen ${\displaystyle \lfloor x\rfloor }$ för något reellt tal x är det största heltal som är mindre än eller lika med x (för positiva tal x ger golvfunktionen helt enkelt heltalsdelen av x).

Exempel:

• ${\displaystyle \lfloor 2{,}9\rfloor =2}$
• ${\displaystyle \lfloor 2\rfloor =2}$
• ${\displaystyle \lfloor -2{,}5\rfloor =-3}$

Andra beteckningssätt är ${\displaystyle \operatorname {floor} (x)}$ (av engelska floor ’golv’) och ${\displaystyle \left[x\right]\ }$

Takfunktionen ${\displaystyle \lceil x\rceil }$ ger på motsvarande sätt det minsta heltal som är större än eller lika med x.

Exempel:

• ${\displaystyle \lceil 2{,}1\rceil =3}$
• ${\displaystyle \lceil 2\rceil =2}$
• ${\displaystyle \lceil -2{,}5\rceil =-2}$

Ett annat beteckningssätt är ${\displaystyle \operatorname {ceil} (x)}$ (av engelska ceiling ’(inner)tak’).

Srinivasa Aiyangar Ramanujan presenterade följande problem i Journal of the Indian Mathematical Society.^[1]

Om n är ett positivt heltal, bevisa att

(i)     ${\displaystyle \left\lfloor {\tfrac {n}{3}\right\rfloor +\left\lfloor {\tfrac {n+2}{6}\right\rfloor +\left\lfloor {\tfrac {n+4}{6}\right\rfloor =\left\lfloor {\tfrac {n}{2}\right\rfloor +\left\lfloor {\tfrac {n+3}{6}\right\rfloor }$

(ii)     ${\displaystyle \left\lfloor {\tfrac {1}{2}+{\sqrt {n+{\tfrac {1}{2}\right\rfloor =\left\lfloor {\tfrac {1}{2}+{\sqrt {n+{\tfrac {1}{4}\right\rfloor }$

(iii)     ${\displaystyle \left\lfloor {\sqrt {n}+{\sqrt {n+1}\right\rfloor =\left\lfloor {\sqrt {4n+2}\right\rfloor .}$

Talet n är ett primtal om och endast om^[2]

${\displaystyle \sum _{m=1}^{\infty }\left(\left\lfloor {\frac {n}{m}\right\rfloor -\left\lfloor {\frac {n-1}{m}\right\rfloor \right)=2.}$

Låt r > 1 vara ett heltal, p_n det n-te primtalet, och

${\displaystyle \alpha =\sum _{m=1}^{\infty }p_{m}r^{-m^{2}.}$

Då är^[3]

${\displaystyle p_{n}=\left\lfloor r^{n^{2}\alpha \right\rfloor -r^{2n-1}\left\lfloor r^{(n-1)^{2}\alpha \right\rfloor .}$

Det finns ett tal θ = 1.3064... (Mills konstant) så att

${\displaystyle \left\lfloor \theta ^{3}\right\rfloor ,\left\lfloor \theta ^{9}\right\rfloor ,\left\lfloor \theta ^{27}\right\rfloor ,\dots }$

är alla primtal.^[4]

Det finns även ett tal ω = 1.9287800... med egenskapen att

${\displaystyle \left\lfloor 2^{\omega }\right\rfloor ,\left\lfloor 2^{2^{\omega }\right\rfloor ,\left\lfloor 2^{2^{2^{\omega }\right\rfloor ,\dots }$

är alla primtal.^[4]

Om π(x) är antalet primtal mindre eller lika stora som x, får man följande formel som en enkel konsekvens av Wilsons sats:^[5]

${\displaystyle \pi (n)=\sum _{j=2}^{n}\left\lfloor {\frac {(j-1)!+1}{j}-\left\lfloor {\frac {(j-1)!}{j}\right\rfloor \right\rfloor .}$

Om n ≥ 2, är^[6]

${\displaystyle \pi (n)=\sum _{j=2}^{n}\left\lfloor {\frac {1}{\sum _{k=2}^{j}\left\lfloor \left\lfloor {\frac {j}{k}\right\rfloor {\frac {k}{j}\right\rfloor }\right\rfloor .}$

Ingen av formlerna i denna sektion är dock av någon praktisk betydelse.^[7][8]

• Stegfunktion/trappfunktion

• Wikimedia Commons har media som rör Golv- och takfunktionerna.
  Bilder & media