Kuark
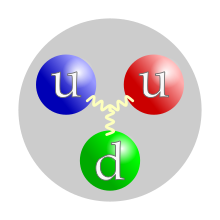 İki yukarı kuark ve bir aşağı kuark ile bunları birbirine bağlayan kuvvetleri oluşturan gluonlardan meydana gelen bir proton. Kuarkların renk yükleri rastgele seçilmiştir; ancak bu renklerin tamamının bulunması zorunludur. | |
| Bileşim | Temel parçacık |
|---|---|
| İstatistik | Fermiyonik |
| Nesil | 1., 2., 3. |
| Etkileşim(ler) | Elektromanyetizma, kütleçekim, güçlü, zayıf |
| Sembol | q |
| Antiparçacık | Antikuark ( q ) |
| Teorileştirme |
|
| Keşif | SLAC Ulusal Hızlandırıcı Laboratuvarı (c. 1968) |
| Türler | 6 (yukarı, aşağı, garip, tılsım, üst ve alt) |
| Elektrik yükü | +2⁄3 e, -1⁄3 e |
| Renk yükü | Evet |
| Spin | 1⁄2 |
| Baryon sayısı | 1⁄3 |
Kuark, bir tür temel parçacık ve maddenin temel bileşenlerinden biridir. Kuarklar, bir araya gelerek hadronlar olarak bilinen bileşik parçacıkları oluşturur. Bunların en kararlıları, atom çekirdeğinin bileşenleri proton ve nötrondur. Renk hapsi olarak bilinen olgudan ötürü kuarklar asla yalnız bir şekilde bulunmaz, yalnızca baryonlar ve mezonlar gibi hadronlar dahilinde bulunabilir. Bu sebeple kuarklar hakkında bilinenlerin çoğu hadronların gözlenmesi sonucunda elde edilmiştir.
Kuarklar; elektrik yükü, renk yükü, spin ve kütle gibi çeşitli yapısal özelliklere sahiptir. Kuarklar, parçacık fiziğinin Standart Model'inde dört temel kuvvetin (elektromanyetizma, kütleçekim, güçlü etkileşim ve zayıf etkileşim) tümüyle de etkileşen, aynı zamanda elektrik yükü temel yükün tam sayı katı olmayan tek temel parçacık ailesidir.
Yukarı, aşağı, tılsım, garip, üst ve alt olmak üzere çeşni olarak bilinen altı tip kuark bulunur. Yukarı ve aşağı kuark, bütün kuarklar içinde en düşük kütleli olanlardır. Daha ağır kuarklar parçacık bozunması yoluyla aşağı ve yukarı kuarka dönüşür, yani yüksek kütle durumundan daha düşük kütle durumuna dönüşüm yaşanır. Bu sebeple yukarı ve aşağı kuarklar evrende en yaygın olarak bulunanlardır. Bununla birlikte tılsım, garip, üst ve alt kuarklar sadece yüksek enerjili çarpışmalarda (kozmik ışınlar ve parçacık hızlandırıcılarda) oluşabilir. Her kuark çeşnisi için ona karşılık gelen bir tane de antiparçacık bulunur. Antikuark denilen bu parçacık, bazı özelliklerinin aynı büyüklükte fakat ters işaretli olması ile kuarktan ayrılır.
Kuark modeli, 1964'te Murray Gell-Mann ve George Zweig tarafından birbirlerinden bağımsız olarak ortaya atıldı. Kuarklar, hadronlar için oluşturulan bir düzenleme şemasının parçaları olarak tanımlandı. Stanford Doğrusal Hızlandırıcı Merkezinde (günümüzdeki adıyla SLAC Ulusal Hızlandırıcı Laboratuvarı) 1968 yılında yapılan ve sonuçları 1969'da yayımlanan derin inelastik saçılma deneyleriyle birlikte kuarkların varlığı fiziksel olarak kanıtlandı. Zaman içinde altı çeşninin tamamı, gerçekleştirilen hızlandırıcı deneyleriyle ispat edildi. Keşfedilen son kuark olan üst kuarkın keşfi ise 1995'te, Fermilab'da gerçekleşti.
Sınıflandırma

Standart Model, günümüz itibarıyla bilinen tüm temel parçacıkları açıklayan bir teoridir.[1] Bu model kuarkların (q); yukarı (u), aşağı (d), tılsım (c), garip (s), üst (t) ve alt (b) olmak üzere altı çeşnisini de kapsar.[2] Kuarkların antiparçacıklarına antikuark denir ve karşılık gelen kuarkın sembolünün üzerine çizgi eklenerek gösterilir (örneğin yukarı kuark için anti kuark u ile gösterilir). Antimaddelerin genelinde olduğu gibi, antikuarklar da kendi kuarkı ile aynı kütleye, ortalama ömre ve spine sahip olsa da elektrik yükü ve diğer yükleri ters işaretlidir.[3]
Kuarklar, spin 1⁄2 parçacıklarıdır ve bu da onların spin-istatistik teoremine göre fermiyon olarak tanımlanmasına yol açar. Dolayısıyla aynı iki fermiyonun aynı anda aynı kuantum durumunda bulunamayacağını söyleyen Pauli dışarlama ilkesine tabiidirler. Bu aynı kuantum durumunda çoklu sayılarda bulunabilen bozonların (tam sayı spinli parçacıklar) tersidir.[4] Leptonlardan farklı olarak kuarklar, güçlü etkileşime girmelerini sağlayan renk yüküne sahiptirler. Farklı kuarklar arasındaki etkileşim, hadronlar olarak bilinen bileşke parçacıkların oluşmasını sağlar.[5]
Hadronların kuantum sayılarını belirleyen kuarklara değerlik kuark denir. Bununla birlikte hadronlar, kuantum sayısına etki etmeyen sonsuz sayıda sanal (veya deniz) kuark, antikuark ve gluon barındırabilir.[6] Üç değerlik kuarklı baryonlar ve bir değerlik kuark ile bir antikuarklı mezonlar olmak üzere iki farklı hadron ailesi vardır.[7] En yaygın görülen baryonlar, atom çekirdeğini oluşturan proton ve nötrondur.[8] Hadronların büyük bir bölümü bilinirken (baryonlar listesi ile mezonlar listesi maddelerine bakınız) bunların çoğu kuark bileşenleri ve yapıtaşını oluşturan kuarkların kazandırdığı özelliklerle ayırt edilirler.[a][9] Varlıkları, kuark modelinin oluşturulmasından beri tahmin edilen daha fazla değerlik kuarka sahip egzotik hadronlar olan pentakuarklar (
q
q
q
q
q
) 2015 yılında LHCb deneyi sırasında keşfedilirken[10] tetrakuarkların (
q
q
q
q
) varlığı henüz ispatlanamamıştır.[11][12]
Temel fermiyonlar, her biri ikişer lepton ve kuarkı kapsayan üç nesilden oluşur. Birinci nesilde yukarı ve aşağı kuark, ikinci nesilde tılsım ve garip kuark, üçüncü nesilde üst ve alt kuark yer alır. Kuarkların ve diğer temel fermiyonların dördüncü nesli ile ilgili araştırmaların tamamı başarısızlıkla sonuçlanmış[13] ve üç nesilden fazlası olmadığına dair doğrudan olmayan kanıtlar mevcuttur.[b][14][15] Daha yüksek nesillerde yer alan parçacıkların genellikle daha büyük kütleye ve daha az kararlılığa sahip olmaları, zayıf etkileşimler vasıtasıyla bozunarak daha küçük nesilli parçacıklara dönüşmesine yol açar. Sadece birinci nesildeki (yukarı ve aşağı) kuarklar doğada yaygın olarak bulunur. Daha ağır kuarklar sadece yüksek enerjili çarpışmalarda (kozmik ışınları içerenler gibi) yaratılabilir ve hemen ardından bozunur. Ancak bu parçacıkların, evrenin daha sıcak ve yoğun fazda olduğu Büyük Patlama'dan sonraki bir saniyenin ilk kesirlerin de bulundukları düşünülür (kuark dönemi). Ağır kuarklar üzerine çalışmalar, parçacık hızlandırıcılar gibi yapay olarak yaratılmış koşullarda yürütülür.[16]
Elektrik yükü, kütle, renk yükü ve çeşniye sahip olan kuarklar çağdaş fiziğin dört temel kuvveti olan elektromanyetizma, kütleçekim, zayıf etkileşim ve güçlü etkileşimin tamamıyla etkileştiği bilinen tek parçacık ailesidir.[8] Ancak kütleçekim, görece daha büyük enerji (Planck enerjisi) veya daha uzun mesafe (Planck uzunluğu) görülen durumların dışında atomik skalada etkisizdir. Geçerli bir kuantum kütleçekimi teorisi var olmadığından, kütleçekim Standart Model ile açıklanamaz.
Geçmişi
Kuark modeli 1964'te, Murray Gell-Mann[17] ve George Zweig[18][19] tarafından, birbirlerinden bağımsız olarak ortaya atıldı.[20] Öneri, Gell-Mann'ın 1961'de hazırladığı sekiz katlı yol ya da daha teknik bir ifadeyle SU(3) çeşni simetrisi olarak bilinen bir parçacık sınıflandırma sistemi formülasyonundan sonra geldi.[21][22] Yuval Ne'eman da aynı yıl, bağımsız bir şekilde sekiz katlı yola benzer bir şema geliştirdi.[23][24]
Kuark teorisi ortaya çıktığında, diğer parçacıklarla birlikte çok sayıda hadron da "particle zoo" dahilindeydi. Gell-Mann ve Zweig hadronların temel parçacık olmadıklarını, onun yerine kuarklar ve antikuarklardan oluşan bileşik parçacıklar olduklarını ortaya attılar. Modelleri; spin ve elektrik yüklerini tanımladıkları yukarı, aşağı ve garip kuark olmak üzere üç çeşniyi kapsıyordu.[17][18][19] Önermeye fizik camiasından gelen ilk tepkiler karışıktı. Kuarkların fiziksel bir varlık mı yoksa o zaman için tam olarak anlaşılmayan bazı kavramların açıklanabilmesi için kullanılan bir soyutlama mı olduğu konusunda bir fikir ayrılığı vardı.[25]
Bir yıl geçmeden Gell-Mann-Zweig modeli için birtakım genişlemeler önerildi. Sheldon Glashow ve James Bjorken, "tılsım" adını verdikleri kuarkların dördüncü çeşnisinin varlığını tahmin ettiler. Bu ekleme; yeni çeşninin zayıf etkileşimin (bu mekanizma kuarkların bozunmasına izin verir) daha iyi açıklanabilmesine olanak sağladığından, bilinen kuark sayısı ile bilinen lepton sayısını eşitlediğinden ve bilinen mezonların kütlelerinin doğru bir şekilde yeniden belirlenmesini sağlayan bir kütle formülü belirttiğinden dolayı önerilmişti.[26]
Stanford Doğrusal Hızlandırıcı Merkezinde (SLAC) 1968 yılında yapılan ve sonuçları 1969'da yayımlanan derin inelastik saçılma deneyleri, protonun daha küçük, nokta benzeri parçacıklardan oluştuğunu ve böylece bir temel parçacık olmadığını gösterdi.[27][28] O dönemde fizikçiler bu nesneleri kuarklar ile ilişkilendirmek konusunda tereddütlü olduklarından parçacıklar, Richard Feynman'ın türettiği "parton" olarak adlandırdı.[29][30][31] Bu deneyler sırasında gözlemlenen cisimler, diğer çeşnilerin de keşfedilmesiyle daha sonra yukarı ve aşağı kuark olarak tanımlanacaktı.[32] Buna rağmen parton, hadronların bileşenlerini (kuarklar, antikuarklar ve gluonlar) tanımlayan ortak bir terim olarak kullanımda kaldı.
Garip kuarkın varlığı SLAC'deki saçılma deneyleri ile dolaylı olarak doğrulandı. Bu, Gell-Mann ve Zweig'ın üç kuark modelinin gerekli bileşeni olmasının yanı sıra, 1947'de kozmik ışınlarda keşfedilen kaon (K) ve pion (π) hadronları için de açıklama getiriyordu.[33] 1970'teki bir araştırmada Glashow, Yannis İliopulos ve Luciano Maiani; çeşni değiştiren nötr akımları açıklayan GIM mekanizmasını ortaya attı. Bu teorik model, henüz keşfedilmemiş tılsım kuarkın varlığına dair yeni kanıtlar oluşturuyordu.[34][35] Var olması gerektiği düşünülen kuark çeşnisi sayısı 1973 yılında, Makoto Kobayashi ve Toshihide Maskawa başka bir kuark çifti olmasının, CP ihlalinin deneysel gözlemiyle açıklanabileceğini ifade etmesiyle altıya yükseldi.[36]
Tılsım kuarklar Kasım 1974'te, Burton Richter önderliğindeki ekip tarafından SLAC'ta ve Samuel C. C. Ting önderliğindeki ekip tarafından Brookhaven Ulusal Laboratuvarı'nda gerçekleştirilen farklı ve bağımsız deneylerde ilk kez tespit edildi. Tılsım kuarklar; mezonlarda, tılsım antikuarklara bağlı bir şekilde gözlemlendi. Keşfedilen meon için Ting'in J, Richter'ın ise ψ (psi) sembolünü kullanması nedeniyle mezonun resmî adı J/psi mezonu oldu. Bu keşifle birlikte kuark modelinin geçerliliği kabul görüldü.[31]
İlerleyen yıllarda, kuark modelinin altı kuarka genişletilmesi için bir takım öneriler getirildi. Bunlardan Haim Harari 1975'teki makalesinde, diğer kuarklar için "üst" ve "alt" terimlerini kullanan ilk kişi oldu.[37][38] Alt kuark 1977'de, Leon Lederman'ın liderliğindeki bir ekip tarafından Fermilab'da gözlemlendi.[39][40] Bu, üst kuarkın varlığına dair bir göstergeydi; zira üst kuarkın yokluğunda alt kuark eşsiz kalmış olacaktı. Üst kuarkın gözlemlenmesi 1995'te, Fermilab'daki CDF[41] ve DØ[42] takımları tarafından gerçekleştirilen deneylerde yaşandı.[20] Bu kuarkın kütlesi, daha önce öngörülenden daha büyüktü.[43][44]
Etimoloji
Gell-Mann quark (İngilizcede "kuark"ın karşılığı) kelimesini, martıların çıkardığı sesten türetmişti.[45] James Joyce'un Finneganın Vahı (Finnegans Wake) adlı kitabındaki bir şiirde yer alan quark kelimesine rastlayana dek, kavram için kullanmayı düşündüğü bu sesin gerçekteki yazımı konusunda kararsız kalmıştı:[46]
Sayın Numune Mark için üç kuark!
Havlaması pek dişli olmasa da
Ve tabii varı yoğu konuya dair değil.— İngilizce: Three quarks for Muster Mark!
Sure he hasn't got much of a bark
And sure any he has it's all beside the mark.
Almanca kökenli olan kelime, bu dilde bir süt ürünü anlamına gelmesinin yanı sıra "saçmalık" anlamı da taşır.[47][48] The Quark and the Jaguar adlı kitabında Gell-Mann, kuark adıyla ilgili daha ayrıntılı bilgi verir:[49]
1963'te çekirdeği oluşturan temel bileşenlere "kuark" (quark) adını verdiğimde, elimde yazı yok sadece "kwork" gibi bir ses vardı. Sonra arada bir dikkatle okuduğum James Joyce'un Finnegans Wake kitabında, "Three quarks for Muster Mark" cümlesinde "quark" sözcüğüyle karşılaştım. "Quark" (anlamı, bir şey için martının ağlaması) "Mark" ve "bark" (havlama sesi) ile ve bunlara benzer sözcüklerle kafiyeli olduğundan, sözcüğü "kwork" şeklinde telaffuz edebilmek için bir bahane bulmalıydım. Ancak kitap Humphrey Chimpden Earwicker adlı bir politikacının rüyasını gösteriyordu. Metindeki sözcükler, Aynanın İçinden (Through the Looking-Glass) kitabındaki birleşik sözcükler gibi genel olarak aynı anda birkaç farklı sözcükten türetilmişti.
Zweig, teorileştirdiği parçacığın dört türü olduğunu düşündüğünden bu parçacık için ace (İngilizcede "as"ın karşılığı) ismini tercih etse de kuark modeli yaygın bir şekilde kabul görünce Gell-Mann'ın kullandığı terim kabul gördü.[50]
Kuark çeşnilerinin isimleri ise farklı nedenlere bağlı olarak verildi. Yukarı ve aşağı kuarklar, taşıdıkları izospinin yukarı ve aşağı bileşenleri olduklarında dolayı bu isimleri aldılar.[51] Garip kuarklar, kuark modeli ortaya çıkmadan yıllar önce kozmik ışınlarda keşfedilen garip parçacıkların bileşenleri olarak keşfedildiklerinde bu şekilde isimlendirildiler ve bu parçacıklar olağandışı uzun yaşam sürelerine sahip oldukları için "garip" olarak anılmaya başladılar.[52] Bjorken ile birlikte tılsım kuark fikrini ortaya atan Glashow, "çalışmamıza charmed quark (İngilizcede "tılsım kuark"ın karşılığı) adını verdik çünkü onun çekirdek altı dünyaya taşıdığı simetriyle büyülenmiş ve sevinmiştik" dedi.[53] Alt ve üst kuark isimleri Harari tarafından, "yukarı ve aşağı kuarkların mantıksal eşleri" oldukları için seçildi.[37][38][52] Geçmişte üst ve alt kuarklar, sırasıyla "gerçeklik" ve "güzellik" isimleriyle de anıldı ancak bu isimler büyük ölçüde kullanımdan kalktı.[54]
Yapısı
Elektrik yükü
Kuarklar kesirli elektrik yüküne sahiptir ve bu değer, çeşnisine bağlı olarak temel yükün (e) -1⁄3 ya da +2⁄3 katı olabilir. Yukarı tip kuark adı verilen yukarı, tılsım ve üst kuarkların elektrik yükü +2⁄3 iken; aşağı tip kuarklar olarak adlandırılan aşağı, garip ve alt kuarklar -1⁄3 elektrik yüküne sahiptir. Antikuarklar, eşlerinin tersi elektrik yüküne; yukarı tip antikuarklar -2⁄3 ve aşağı tip antikuarklar 1⁄3 elektrik yüküne sahiptir. Bir hadronun elektrik yükü, barındırdığı kuarkların elektrik yükleri toplamına eşit olduğundan bütün hadronlar tam sayı yüklere sahiptirler. Üç kuarkın (baryonlar), üç antikuarkın (antibaryonlar) ve bir kuark ve bir antikuarkın (mezonlar) kombinasyonu her zaman tam sayı değerini verir.[55] Örneğin atom çekirdeğinin bileşenlerinden iki aşağı kuark ve bir yukarı kuarktan oluşan nötron 0, iki yukarı kuark ve bir aşağı kuarktan oluşan proton ise +1 elektrik yüküne sahiptir.[8]
Spin
Spin büyüklüğü, indirgenmiş Planck sabiti ħ biriminden olan bir vektörle gösterilebilir. Kuarklar için herhangi bir eksen boyunca spin vektörü bileşeninin ölçümü yalnızca +ħ/2 ya da -ħ/2 değerlerini verebildiğinden kuarklar spin 1⁄2 parçacıklar olarak sınıflandırılır.[56] Spinin verilen bir eksendeki -genel kabulle z eksenindeki- bileşeni, +1⁄2 değeri için yukarı ok ↑ işareti ile ve -1⁄2 değeri için aşağı ok işareti ile ifade edilir. Örneğin z ekseni boyunca spini +1⁄2 olan bir yukarı kuark u↑ ile ifade edilir.[57]
Zayıf etkileşim

Bir çeşninin kuarkı, başka bir çeşninin kuarkına sadece, parçacık fiziğindeki dört temel kuvvetten biri olan zayıf etkileşim ile dönüşebilir. W bozonu yayımı veya soğurulması yoluyla herhangi bir türden yukarı tip kuark (yukarı, tılsım ve üst kuarklar) herhangi bir türden aşağı tip kuarka (aşağı, garip ve alt kuarklar) dönüşebilir ya da bu dönüşümün tersi gerçekleşebilir. Bu çeşni dönüşüm mekanizması, bir nötronun (n), bir proton (p), bir elektron (e-) ve bir elektron antinötrinosuna (ve) ayrıldığı beta bozunması radyoaktif sürecine sebep olur (sağ kısımdaki diygram). Bu olay nötrondaki (udd) aşağı kuarklardan birinin sanal bir W- parçacığı yayarak bir yukarı kuarka dönüşmesi ile olur. Sonuçta nötron protona (uud) dönüşür. Sonrasında W- bozonu da bir elektron ve bir elektron antinötrinosuna dönüşür.[58]
| n | → | p + e + ve | (Beta bozunması, hadron gösterimi) |
| udd | → | uud + e + ve | (Beta bozunması, kuark gösterimi) |
Beta bozunması ve onun tersi olan süreç olan ters beta bozunması, pozitron emisyon tomografisi (PET) gibi tıbbi uygulamalarda ve nötrino keşfi gibi yüksek enerji deneylerinde kullanılır.

Çeşni dönüşüm süreci bütün kuarklar için aynı iken her kuark kendi neslinden bir kuarka dönüşme eğilimindedir. Bütün çeşni dönüşümleri için göreli eğilimler Cabibbo-Kobayashi-Maskawa matrisi (CKM matrisi) olarak bilinen bir matematik tablosu ile tanımlanır. CKM matrisi elemanlarının yaklaşık değerleri şu şekildedir:[59]
Buradaki Vij, i çeşnili kuarkın j çeşnili kuarka (veya tam tersi) dönüşümünün eğilimini gösterir.[c]
Leptonlar (yukarıdaki beta bozunması diyagramındaki W bozonunun sağı tarafı) için de bunun eşdeğeri olan Pontecorvo-Maki-Nakagawa-Sakata matrisi (PMNS matrisi) bulunur.[60] CMK ve PMNS matrisleri birlikte bütün çeşni dönüşümlerini tanımlar ancak ikisi arasındaki bağlantı henüz net değildir.[61]
Güçlü etkileşim ve renk yükü

Kuantum renk dinamiğine göre kuarklar, renk yükü olarak adlandırılan bir özelliğe sahiptir. Renk yükünün mavi, yeşil ve kırmızı olmak üzere rastgele belirlenmiş üç türü bulunur.[d] Bunlardan her biri, sırasıyla antimavi, antiyeşil ve antikırmızı olmak üzere birer antirenk ile tamamlanır. Her kuark bir renk taşırken her antikuark da bir antirenk taşır.[62]

Üç rengin farklı kombinasyonları ile yüklenmiş kuarklar arasındaki çekme ve itme sistemi güçlü etkileşim olarak adlandırılır. Güçlü etkileşime, gluonlar denilen kuvvet taşıyıcı parçacıklar aracılık eder. Güçlü etkileşimi tanımlayan teori kuantum renk dinamiğidir. Herhangi bir renk değeri ile yüklenmiş bir kuark, ona karşılık gelen antirengi taşıyan antikuarkla birlikte bir bağlı sistem oluşturabilir; üç (anti)kuark, birer (anti)renk benzer şekilde bağ oluşturacaktır. İki çekici kuarkın sonucu renk nötrlüğü olacaktır ve renk yükü ξ olan bir kuark ile -ξ olan bir antikuarkın bir araya gelmesi 0 renk yükü (veya beyaz renk) ve bir mezon oluşumu şeklinde sonuçlanacaktır. Optikteki eklemeli renk modeline benzer şekilde, her biri farklı renkten olan üç kuarkın veya üç antikuarkın kombinasyonu da beyaz renk yükü ve bir baryon veya antibaryon oluşumu şeklinde sonuçlanacaktır.[63]
Modern parçacık fiziğinde ayar simetrileri, parçacıklar arası etkileşimlerle ilgilidir. SU(3) (genellikle SU(3)c şeklinde kısaltılır) rengi, kuarklardaki renk yüküyle ilgili ayar simetrisidir ve kuantum renk dinamiği için tanımlayıcı simetridir.[64] Kuantum renk dinamiğinin fiziği, üç boyutlu renk uzayında hangi yönlerin mavi, kırmızı ya da yeşil olarak tanındığından bağımsızdır. SU(3)c renk dönüşümleri renk uzayındaki dönmelere denk gelir (matematiksel ifadeyle bir karmaşık uzay). Kuarkların renklerine göre fB, fG, fR[65] alt türleri olan her kuark çeşnisi (f) bir triplet oluşturur: SU(3)c'ün temel temsili altında dönüşen üç bileşenli bir kuantum alanı.[66] SU(3)c'ün yerel olması, güçlü etkileşimin özelliklerini, bilhassa kuvvet taşıyıcıları olarak sekiz gluon türünün varlığını belirler.[64][67]
Kütle

Kuarkların kütleleri, kuarkın kendi başına olan kütlesini ifade eden çıplak kuark kütlesi ile, kuarkın ve onu çevreleyen gluon parçacık alanının kütlesinin toplamını ifade eden bileşik kuark kütlesi olmak üzere iki farklı şekilde gösterilir.[68] Çoğu hadronun kütlesi, kuarkların kütlelerinden ziyade kuarkları bir arada tutan gluonların kütlelerinden gelir. Gluonlar tabiatları gereği kütlesiz olurken sahip oldukları enerji (özellikle kuantum renk dinamiği bağlanma enerjisi), hadronların kütlelerinin çoğunluğunu oluşturur. Örneğin protonun 938 MeV/c2 olan durgun kütlesine, bileşeni oluşturan üç değerlik kuarkın katkısı 11 MeV/c2 iken geriye kalanın çoğu gluonların kuantum renk dinamiği bağlanma enerjisine atfedilebilir.[69][70]
Standart Model'e göre temel parçacıkların kütleleri, Higgs bozonu ile bağlantılı olan Higgs mekanizmasından kazanır. Fizikçiler, kütlesi (~171 GeV/c2) olan[69][71] üst kuarkın kütlesi üzerine yapılacak olan ilerdeki araştırmaların kuarkların ve diğer temel parçacıkların kütlelerinin orijinine dair daha fazla bilgi vereceğini düşünürler.[72][73]
Özellikler tablosu
Aşağıdaki tablo altı kuarkın başlıca yapısal özelliklerini özetler. Çeşni kuantum sayıları (izospin (I3), tılsım (C), gariplik (S), üstlük (T) ve altlık (B′)) belli kuark çeşnilerine atanmıştır ve kuark temelli sistemlerin ve hadronların niteliklerini gösterir. Baryonlar üç kuarktan oluştuğundan, baryon sayısı (B) bütün kuarklar için +1⁄3'tür. Antikuarklar için elektrik yükü (Q) ve diğer bütün çeşni kuantum sayıları (B, I3, C, S, T ve B′) ters işaretlidir. Kütle ve toplam açısal momentum kuantum sayısı (J; nokta parçacıklar için spine eşittir) antikuarklarda işaret değiştirmez.
| Adı | Sembolü | Kütlesi (MeV/c2)* | J | B | Q (e) | I3 | C | S | T | B′ | Antipaçacık | Antiparçacık sembolü |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Birinci nesil | ||||||||||||
| Yukarı | u | 2,3 ± 0,7 ± 0,5 | 1⁄2 | +1⁄3 | +2⁄3 | +1⁄2 | 0 | 0 | 0 | 0 | Antiyukarı | u |
| Aşağı | d | 4,8 ± 0,5 ± 0,3 | 1⁄2 | +1⁄3 | -1⁄3 | -1⁄2 | 0 | 0 | 0 | 0 | Antiaşağı | d |
| İkinci nesil | ||||||||||||
| Tılsım | c | 1275±25 | 1⁄2 | +1⁄3 | +2⁄3 | 0 | +1 | 0 | 0 | 0 | Antitılsım | c |
| Garip | s | 95±5 | 1⁄2 | +1⁄3 | -1⁄3 | 0 | 0 | -1 | 0 | 0 | Antigarip | s |
| Üçüncü nesil | ||||||||||||
| Üst | t | 173210±510 ± 710 | 1⁄2 | +1⁄3 | +2⁄3 | 0 | 0 | 0 | +1 | 0 | Antiüst | t |
| Alt | b | 4180±30 | 1⁄2 | +1⁄3 | -1⁄3 | 0 | 0 | 0 | 0 | -1 | Antialt | b |
*173210±510 ± 710 gibi gösterimler ölçüm kesinsizliğini belirtir.
Etkileşen kuarklar
Kuantum renk dinamiğinin tanımladığı gibi kuarklar arasındaki güçlü etkileşime, gluonlar olarak bilinen kütlesiz vektör ayar bozonları aracılık eder. Her bir gluon, birer renk yükü ile antirenk yükü taşır. Parçacık etkileşimlerinin standart referans sisteminde gluonlar, kuarklar arasında sürekli olarak sanal emisyon ve absorbsiyon yolları ile takas edilir. Bir gluon kuarklar arasında taşındığında, hem kuarkta hem de gluonda renk değişimi olur. Örneğin bir kırmızı kuark bir kırmızı-antiyeşil gluon yayarsa, yeşile ya da bir yeşil kuark bir kırmızı-antiyeşil gluon soğurursa kırmızıya dönüşür. Böylece, her kuarkın rengi sürekli değişirken güçlü etkileşim korunmuş olur.[74][75][76]
Gluonlar renk taşıdıklarından, diğer gluonları yayma ve soğurma yetisine sahiptirler. Bu da asimptotik özgürlük olarak adlandırılan kuarkların birbirlerine yakınlaşırken aralarındaki renk dinamiği bağlanma kuvvetinin zayıflamasına sebep olur.[77] Diğer taraftan kuarklar arasındaki mesafe arttığında bağlanma kuvveti de güçlenir. Renk alanı gerilmiş bir hâle gelir ve alanı güçlendirmek için uygun renkten daha çok gluon kendiliğinden yaratılır. Belli enerji eşiğinin üzerinde kuark ve antikuark çiftleri üretilir. Çiftler, ayrılmış kuarklar ile bağlanır ve yeni hadronların oluşmasına sebep olur. Kuarkların hiçbir zaman izole bir şekilde görülemeyeceğini söyleyen bu olgu renk hapsi olarak tanımlanır.[78][79] Bu hadronlaşma süreci, yüksek enerjili çarpışmalarda oluşan kuarkların bir başka yolla etkileşime girmeye başlamasından önce meydana gelir. Buradaki tek istisna, hadronize olmadan önce bozunmaya uğrayabilen üst kuarktır.[80]
Deniz kuarkları
Hadronlar, kuantum sayılarına katkıda bulunan değerlik kuarklar (qv) ile birlikte, deniz kuarkları (
q
s) olarak bilinen sanal kuark-antikuark (qq) çiftleri içerir. Sanal kuark-antikuark çiftleri, hadronlardaki değerlik kuarkların çevresinde bir çeşit "bulut" veya "zırh" olarak nitelendirilebilecek biçimde olma eğilimindedir. Bu bulut sanal gluonlardan oluşan dıştaki başka bir katmanla tamamlanır. Bu katmanlar çevrelediği değerlik kuarka göre bir renk alır. Kuantum renk dinamiği, değerlik kuarkın antirengini taşıyan buluttaki sanal antikuarkların alanın içinde daha yakın olmalarını sağlar. Örneğin kırmızı bir kuark için, antikırmızı sanal antikuarklar, kırmızı sanal kuark eşlerinden ziyade kırmızı değerlik kuarka yakınlaşma eğiliminde olacaktır.[81][82]
Kuark maddesinin diğer evreleri

Yeterli düzeyde uç şartlar altında, kuarklar hapisten kurtularak serbest parçacık haline gelebilir. Asimptotik özgürlük boyunca, yüksek sıcaklıkta güçlü etkileşim zayıflar. Nihayetinde renk hapsi kaybolacak ve serbest hareket eden kuarklar ve gluonların son derece sıcak bir plazması oluşabilecektir. Maddenin bu teorik evresine kuark-gluon plazması adı verilir.[85] Bu durum için gerekli olan kesin koşullar bilinmemekle birlikte çeşitli tartışma ve deney konusu olmuştur. 2000'lerdeki tahminler, gerekli sıcaklığın (1,90±0,02)×1012 kelvin olduğunu gösterir.[86] 1980'lerde ve 1990'larda Avrupa Nükleer Araştırma Merkezinde (CERN) yapılan denemelere karşın şimdiye kadar serbest kuarklar ve gluonlar için gereken koşullara hiçbir zaman erişilememiştir. Öte yandan 2000'li yıllarda Göreli Ağır İyon Çarpıştırıcısı'nda gerçekleştirilen deneyler sonucunda "neredeyse kusursuz" akışkan hareketi yapan sıvı benzeri kuark maddesi için kanıtlar bulunmuştur.[87]
Kuark-gluon plazması, ağır kuark çiftlerinin sayı bakımından yukarı ve aşağı kuark çiftlerinden büyük farkla fazla olması ile nitelendirilebilir. Hadronların kararlı olamayacağı kadar yüksek bir sıcaklığa sahip olan Büyük Patlama sonrasındaki 10−6 saniyeden öncesinde, kuark dönemi olarak adlandırılan dönemde, evrenin kuark-gluon plazması ile dolu olduğu düşünülür.[88]
Yeterli düzeyde yüksek baryon yoğunluklarında ve görece düşük sıcaklıklarda kuark maddesinin, zayıf etkileşen kuarkların Fermi sıvısına yozlaşması beklenir. Bu sıvı renkli kuark Cooper çiftlerinin yoğunlaşması ve böylece de yerel SU(3)c simetrisinin kırılması ile karakterize edilebilir. Cooper çiftleri renk yükü barındırdıklarından, buna benzer kuark maddesi evreleri renk süperiletkeni olacaklar; renk yükü, kuark maddesinden hiçbir dirençle karşılaşmadan geçebilecektir.[89]
Notlar
- ^ p ile Δ+ ve n ile Δ0 gibi bazı baryonlar aynı kuark içeriğine sahiptirler. Bu durumlarda Δ parçacıkları proton ve nötronun uyarılmış durumları olarak nitelendirilirler.
- ^ Buna dair ana kanıtı,
Z0
bozonunun rezonans genişliğinin, 4. nesil nötrinoların ~45 GeV/c2 değerinden daha fazla kütleye sahip olmaya zorlaması oluşturur. Bu durum, diğer üç nesil nötrinoların kütlelerinin 2 MeV/c2 değerini geçmemesi durumuyla çelişki gösterir. - ^ Bir kuarkın başka bir kuarka bozunmasının gerçekteki olasılığı; bozunan kuarkın kütlesi, bozunma ürünlerinin kütleleri ve CKM matrisindeki denk gelen elemanın yanı sıra diğer değişkenlerin de dahil olduğu karmaşık bir fonksiyondur. Bu olasılık, denk gelen CKM girişinin büyüklüğünün karesi ile orantılıdır (ancak eşit değildir).
- ^ Adına rağmen renk yükünün, görünür ışığın renk spektrumu ile hiçbir ilişkisi yoktur.
Kaynakça
- Özel
- ^ Amsler, C. et al. (Particle Data Group) (2008). "Higgs Bosons: Theory and Searches" (PDF). Physics Letters B (1 bas.). 667: 1-1340. doi:10.1016/j.physletb.2008.07.018. 1 Şubat 2017 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 25 Şubat 2010.
- ^ Nave, R. "Quarks". HyperPhysics (İngilizce). Georgia Devlet Üniversitesi Fizik ve Astronomi Bölümü. 5 Eylül 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Eylül 2009.
- ^ Wong, S. S. M. (1998). Introductory Nuclear Physics (İngilizce) (2. bas.). Wiley Interscience. s. 30. ISBN 0-471-23973-9.
- ^ Peacock, K. A. (2008). The Quantum Revolution (İngilizce). ABC-CLIO/Greenwood. s. 125. ISBN 031333448X.
- ^ Rathsman, Johan (1996). Quark and Lepton Interactions: Studies of quantum chromodynamics and Majorana neutrinos (PDF) (doktora) (İngilizce). Uppsala Üniversitesi. s. 3. 22 Aralık 2018 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 5 Aralık 2017.
- ^ Povh, B.; Scholz, C.; Rith, K.; Zetsche, F. (2008). Particles and Nuclei (İngilizce). Springer. s. 98. ISBN 3540793674.
- ^ Davies, P. C. W. (1979). "Bölüm 6.1". The Forces of Nature (İngilizce). Cambridge University Press. ISBN 052122523X.
- ^ a b c Munowitz, M. (2005). Knowing (İngilizce). Oxford University Press. s. 35. ISBN 0195167376.
- ^ Serway, Raymond A.; Jewett, John W. (2005). Finding Patterns in the Particles (İngilizce) (4 bas.). Cengage Learning. s. 1067. ISBN 053449143X.
- ^ Aaij, R.; ve diğerleri. (LHCb iş birliği) (2015). "Observation of J/ψp Resonances Consistent with Pentaquark States in Λ0b→J/ψK-p Decays". Physical Review Letters (İngilizce). 115 (7): 072001. arXiv:1507.03414 $2. Bibcode:2015PhRvL.115g2001A. doi:10.1103/PhysRevLett.115.072001.
- ^ Choi, S.-K.; ve diğerleri. (Belle iş birliği) (2007). "Observation of a Resonance-like Structure in the
π±
Ψ′ Mass Distribution in Exclusive B→K
π±
Ψ′ decays". Physical Review Letters (İngilizce). 100 (14): 142001. arXiv:0708.1790 $2. Bibcode:2008PhRvL.100n2001C. doi:10.1103/PhysRevLett.100.142001. - ^ Aaij, R.; ve diğerleri. (LHCb iş birliği) (2014). "Observation of the Resonant Character of the Z(4430)- State". Physical Review Letters (İngilizce). 112. arXiv:1404.1903 $2. Bibcode:2014PhRvL.112v2002A. doi:10.1103/PhysRevLett.112.222002.
- ^ Amsler, C. et al. (Particle Data Group) (2008). "Review of Particle Physics: b′ (4th Generation) Quarks, Searches for" (PDF). Physics Letters B (İngilizce) (1 bas.). 667: 1-1340. doi:10.1016/j.physletb.2008.07.018. 21 Aralık 2018 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 25 Şubat 2010.
- ^ Decamp, D. (1989). "Determination of the number of light neutrino species". Physics Letters B (İngilizce) (4 bas.). 231: 519. doi:10.1016/0370-2693(89)90704-1.
- ^ Fisher, A. (1991). "Searching for the Beginning of Time: Cosmic Connection". Popular Science (İngilizce) (4. bas.). 238: 70. 14 Ağustos 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 25 Şubat 2010.
- ^ Perkins, D. H. (2003). Particle Astrophysics (İngilizce). Oxford University Press. s. 4. ISBN 0198509529.
- ^ a b Gell-Mann, Murray (1964). "A Schematic Model of Baryons and Mesons". Physics Letters (İngilizce) (3 bas.). 8: 214-215. doi:10.1016/S0031-9163(64)92001-3.
- ^ a b Zweig, G. (1964). "An SU(3) Model for Strong Interaction Symmetry and its Breaking". CERN Report No.8181/Th 8419 (İngilizce).
- ^ a b Zweig, G. (1964). "An SU(3) Model for Strong Interaction Symmetry and its Breaking: II". CERN Report No.8419/Th 8412 (İngilizce).
- ^ a b Carithers, B.; Grannis, P. (1995). "Discovery of the Top Quark" (PDF). Beam Line (İngilizce) (3 bas.). SLAC Ulusal Hızlandırıcı Laboratuvarı. 25: 4-16. 3 Aralık 2016 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 25 Şubat 2010.
- ^ Gell-Mann, Murray (2000) [1964]. "The Eightfold Way: A theory of strong interaction symmetry". M. Gell-Manm, Y. Ne'emann (Ed.). The Eightfold Way (İngilizce). Westview Press. s. 11. ISBN 0-7382-0299-1.
- ^ Gell-Mann, Murray (1961), "The Eightfold Way: A theory of strong interaction symmetry", Synchroton Laboratuvarı Rapor CTSL-20 (İngilizce), Kaliforniya Teknoloji Enstitüsü
- ^ Ne'emann, Y. (2000). "Derivation of strong interactions from gauge invariance". Gell-Manm, M.; Ne'emann, Y. (Ed.). The Eightfold Way (İngilizce). Westview Press (1964 tarihinde yayınlandı). ISBN 0-7382-0299-1.
Orijinal Ne'emann, Y. (1961). "Derivation of strong interactions from gauge invariance". Nuclear Physics (İngilizce). 26: 222. doi:10.1016/0029-5582(61)90134-1. - ^ Olby, R. C.; Cantor, G. N. (1996). Companion to the History of Modern Science (İngilizce). Taylor & Francis. s. 673. ISBN 0415145783.
- ^ Pickering, A. (1984). Constructing Quarks (İngilizce). University of Chicago Press. ss. 114-125. ISBN 0226667995.
- ^ Bjorken, B. J.; Glashow, S. L. (1964). "Elementary Particles and SU(4)". Physics Letters (İngilizce). 11 (3): 255-257. Bibcode:1964PhL....11..255B. doi:10.1016/0031-9163(64)90433-0.
- ^ Bloom, E. D. (1969). "High-Energy Inelastic e–p Scattering at 6° and 10°". Physical Review Letters (İngilizce). 23 (16): 930-934. doi:10.1103/PhysRevLett.23.930.
- ^ Breidenbach, M. (1969). "Observed Behavior of Highly Inelastic Electron–Proton Scattering". Physical Review Letters (İngilizce). 23 (16): 935-939. doi:10.1103/PhysRevLett.23.935.
- ^ Feynman, Richard (1969). "Very High-Energy Collisions of Hadrons". Physical Review Letters (İngilizce) (24 bas.). 23: 1415-1417. doi:10.1103/PhysRevLett.23.1415.
- ^ Kretzer; S.; ve diğerleri. (2004). "CTEQ6 Parton Distributions with Heavy Quark Mass Effects". Physical Review D (İngilizce) (11 bas.). 69: 114005. doi:10.1103/PhysRevD.69.114005. arXiv:hep-ph/0307022.
- ^ a b Griffiths 2008, s. 42.
- ^ Peskin & Schroeder 1995, s. 556.
- ^ Ezhela, V. V. (1996). Particle Physics (İngilizce). Springer. s. 2. ISBN 1563966425.
- ^ Glashow, S. L.; İliopulos, Y.; Maiani, L. (1970). "Weak Interactions with Lepton–Hadron Symmetry". Physical Review D (İngilizce). 2 (7): 1285-1292. doi:10.1103/PhysRevD.2.1285.
- ^ Griffiths 2008, s. 44.
- ^ Kobayashi, M.; Maskawa, T. (1973). "CP-Violation in the Renormalizable Theory of Weak Interaction". Progress of Theoretical Physics (İngilizce) (2 bas.). 49: 652-65. doi:10.1143/PTP.49.652.
- ^ a b Harari, Haim (1975). "A new quark model for hadrons". Physics Letters B (İngilizce). 57B: 265. doi:10.1016/0370-2693(75)90072-6.
- ^ a b Staley, K. W. (2004). The Evidence for the Top Quark (İngilizce). Cambridge University Press. ss. 31-33. ISBN 9780521827102.
- ^ Herb, S. W.; ve diğerleri. (1997). "Observation of a Dimuon Resonance at 9.5 GeV in 400-GeV Proton-Nucleus Collisions". Physical Review Letters (İngilizce). 39: 252. doi:10.1103/PhysRevLett.39.252.
- ^ Bartusiak, M. (1994). A Positron named Priscilla (İngilizce). National Academies Press. s. 245. ISBN 0309048931.
- ^ Abe, F. et al. (CDF deneyi) (1995). "Observation of Top Quark Production in pp Collisions with the Collider Detector at Fermilab". Physical Review Letters (İngilizce). 74: 2626-2631. doi:10.1103/PhysRevLett.74.2626.
- ^ Abachii, S. et al. (D0 deneyi) (1995). "Search for High Mass Top Quark Production in pp Collisions at √s = 1.8 TeV". Physical Review Letters (İngilizce). 74: 2422-2426. doi:10.1103/PhysRevLett.74.2422.
- ^ Staley, K. W. (2004). The Evidence for the Top Quark (İngilizce). Cambridge University Press. s. 144. ISBN 0521827108.
- ^ "New Precision Measurement of Top Quark Mass" (İngilizce). Brookhaven Ulusal Laboratuvarı. 8 Mayıs 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 26 Şubat 2010.
- ^ Gribbin, J.; Gribbin, M. (1997). Richard Feynman: A Life in Science (İngilizce). Penguin Books. s. 194. ISBN 0-452-27631-4.
- ^ Joyce, James (1982). Finnegans Wake (İngilizce). Penguin Books (1939 tarihinde yayınlandı). s. 383. ISBN 0-14-00-6286-6. LCCN-59-354.
- ^ "What Does 'Quark' Have to Do with Finnegans Wake?" (İngilizce). Merriam-Webster. 27 Haziran 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Haziran 2018.
- ^ Gillespie, Gerald E. P. "Why Joyce Is and Is Not Responsible for the Quark in Contemporary Physics" (PDF). Papers on Joyce 16 (İngilizce). 17 Ocak 2018 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 27 Haziran 2018.
- ^ Gell-Mann, Murray (1995). The Quark and the Jaguar: Adventures in the Simple and the Complex (İngilizce). Henry Holt and Company. s. 180. ISBN 978-0805072532.
- ^ Gleick, J. (1992). Genius: Richard Feynman and Modern Physics (İngilizce). Little, Brown and Company. s. 390. ISBN 0-316-903167.
- ^ Sakurai, J. J. (1994). S. F Tuan (Ed.). Modern Quantum Mechanics (İngilizce) (Gözden geçirilmiş bas.). Addison-Wesley. s. 376. ISBN 0-201-53929-2.
- ^ a b Perkins, D. H. (2000). Introduction to High Energy Physics (İngilizce). Cambridge University Press. s. 8. ISBN 0521621968.
- ^ Riordan, M. (1987). The Hunting of the Quark: A True Story of Modern Physics (İngilizce). Simon & Schuster. s. 210. ISBN 9780671504663.
- ^ Close 2006, s. 133.
- ^ Quigg, Chris (2006). Fraser, G. (Ed.). The New Physics for the Twenty-First Century (İngilizce). Cambridge University Press. s. 91. ISBN 0521816009.
- ^ Close, F. (2006). The New Cosmic Onion (İngilizce). CRC Press. ss. 80-90. ISBN 1584887982.
- ^ Lincoln, D. (2004). Understanding the Universe (İngilizce). World Scientific. s. 116. ISBN 9812387056.
- ^ "Weak Interactions". Virtual Visitor Center (İngilizce). SLAC Ulusal Hızlandırıcı Laboratuvarı. 2008. 23 Kasım 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Şubat 2010.
- ^ Amsler, C.; ve diğerleri. (2008). "Review of Particles Physics: The CKM Quark-Mixing Matrix" (PDF). Physics Letters (İngilizce) (1 bas.). B667: 1-1340. 21 Aralık 2018 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 27 Şubat 2010.
- ^ Maki, Z.; Nakagawa, M.; Sakata, S. (1962). "Remarks on the Unified Model of Elementary Particles". Progress of Theoretical Physics (İngilizce) (5 bas.). 28: 870. doi:10.1143/PTP.28.870. 9 Mayıs 2010 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Ekim 2020.
- ^ Chauhan, B. C.; Picariello, M.; Pulido, J.; Torrente-Lujan, E. (2007). "Quark–lepton complementarity, neutrino and standard model data predict θPMNS13 = 9°+1°
-2°". European Physical Journal (İngilizce) (3 bas.). C50: 573-578. doi:10.1140/epjc/s10052-007-0212-z. arXiv:hep-ph/0605032. - ^ Nave, R. "The Color Force". HyperPhysics (İngilizce). Georgia Devlet Üniversitesi Fizik ve Astronomi Bölümü. 6 Mayıs 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Şubat 2010.
- ^ Schumm, B. A. (2004). Deep Down Things (İngilizce). Johns Hopkins University Press. ss. 131-132. ISBN 080187971X. OCLC 55229065.
- ^ a b Peskin & Schroeder 1995, s. Part III.
- ^ Icke, V. (1995). The Force of Symmetry (İngilizce). Cambridge University Press. s. 216. ISBN 052145591X.
- ^ Han, M. Y. (2004). A Story of Light (İngilizce). World Scientific. s. 78. ISBN 9812560343.
- ^ Sutton, C. "Quantum chromodynamics (physics)". Encyclopædia Britannica Online. 9 Aralık 2010 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Mart 2010.
- ^ Watson, A. (2004). The Quantum Quark (İngilizce). Cambridge University Press. ss. 285-286. ISBN 0521829070.
- ^ a b c Amsler, C. et al. (Particle Data Group) (2008). "Review of Particle Physics: Quarks" (PDF). Physics Letters B (İngilizce) (1 bas.). 667: 1-1340. doi:10.1016/j.physletb.2008.07.018. 21 Aralık 2018 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 12 Mart 2010.
- ^ Weise, W.; Green, A. M. (1984). Quarks and Nuclei (İngilizce). World Scientific. ss. 65-66. ISBN 9971966611.
- ^ McMahon, D. (2008). Quantum Field Theory Demystified (İngilizce). McGraw-Hill. s. 17. ISBN 0071543821.
- ^ Roth, S. G. (2007). Precision Electroweak Physics at Electron–Positron Colliders (İngilizce). Springer. s. VI. ISBN 3540351647.
- ^ Yıldız, Hatice Turan (1 Nisan 2008). "CERN, LHC Deneyinde Top Kuark Üretimi" (PDF). C.B.U. Journal of Science (2. bas.). 4: 187-194. ISSN 1305-1385.[ölü/kırık bağlantı]
- ^ Feynman, R. P. (1985). QED: The Strange Theory of Light and Matter (İngilizce) (1. bas.). Princeton University Press. ss. 136-137. ISBN 0-691-08388-6.
- ^ Veltman, M. (2003). Facts and Mysteries in Elementary Particle Physics (İngilizce). World Scientific. ss. 45-47. ISBN 981238149X.
- ^ Wilczek, F.; Devine, B. (2006). Fantastic Realities (İngilizce). World Scientific. s. 85. ISBN 981256649X.
- ^ Wilczek, F.; Devine, B. (2006). Fantastic Realities (İngilizce). World Scientific. s. 400ff. ISBN 981256649X.
- ^ Veltman, M. (2003). Facts and Mysteries in Elementary Particle Physics (İngilizce). World Scientific. ss. 295-297. ISBN 981238149X.
- ^ Yulsman 2002, s. 55.
- ^ F. Garberson (2008). "Top Quark Mass and Cross Section Results from the Tevatron" (İngilizce). arXiv:0808.0273 $2.
- ^ Steinberger, J. (2005). Learning About Particles (İngilizce). Springer. s. 130. ISBN 3-540-21329-5.
- ^ Wong, C. Y. (1994). Introduction to High-energy Heavy-ion Collisions (İngilizce). World Scientific. s. 149. ISBN 981-02-0263-6.
- ^ Rüester, S. B.; Werth, V.; Buballa, M.; Shovkovy, I. A.; Rischke, D. H. (2005). "The phase diagram of neutral quark matter: Self-consistent treatment of quark masses". Physical Review D (İngilizce). 72: 034003. doi:10.1103/PhysRevD.72.034004. arXiv:hep-ph/0503184.
- ^ Alford, M. G.; Rajagopal, K.; Schaefer, T.; Schmitt, A. (2008). "Color superconductivity in dense quark matter". Reviews of Modern Physics (İngilizce). 80: 1455-1515. doi:10.1103/RevModPhys.80.1455. arXiv:0709.4635.
- ^ Mrowczynski, S. (1998). "Quark–Gluon Plasma" (PDF). Acta Physica Polonica B (İngilizce). 29: 3711. arXiv:nucl-th/9905005. 4 Ağustos 2009 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 18 Mart 2010.
- ^ Fodor, Z.; Katz, S. D. (2004). "Critical point of QCD at finite T and μ, lattice results for physical quark masses". Journal of High Energy Physics (İngilizce). 2004: 50. doi:10.1088/1126-6708/2004/04/050. arXiv:hep-lat/0402006.
- ^ "RHIC Scientists Serve Up "Perfect" Liquid". Brookhaven Ulusal Laboratuvarı. 2005. 16 Temmuz 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 19 Mart 2010.
- ^ Yulsman 2002, s. 75.
- ^ Sedrakian, A.; Clark, J. W.; Alford, M. G. (2007). Pairing in Fermionic Systems (İngilizce). World Scientific. ss. 2-3. ISBN 9812569073.
- Genel
- Close, F. (2006). The New Cosmic Onion (İngilizce). CRC Press. ISBN 1584887982.
- Yulsman, T. (2002). Origins: The Quest for Our Cosmic Roots (İngilizce). CRC Press. ISBN 075030765X.
- Peskin, M. E.; Schroeder, D. V. (1995). An Introduction to Quantum Field Theory (İngilizce). Addison-Wesley. ISBN 0-201-50397-2.
- Griffiths, David (2008). Introduction to Elementary Particles (İngilizce) (2. bas.). Wiley-VCH. ISBN 3527406018.
Konuyla ilgili yayınlar
- Ali, A.; Kramer, G. (2011). "JETS and QCD: A Historical Review of the Discovery of the Quark and Gluon Jets and Its Impact on QCD". European Physical Journal H (İngilizce). 36 (2): 245. arXiv:1012.2288 $2. Bibcode:2011EPJH...36..245A. doi:10.1140/epjh/e2011-10047-1.
- Hughes, Ian Simpson (1985). Elementary Particles (İngilizce) (2. bas.). Cambridge University Press. ISBN 0-521-26092-2.
- Oerter, Robert (2005). The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics (İngilizce). Pi Press. ISBN 0132366789.


