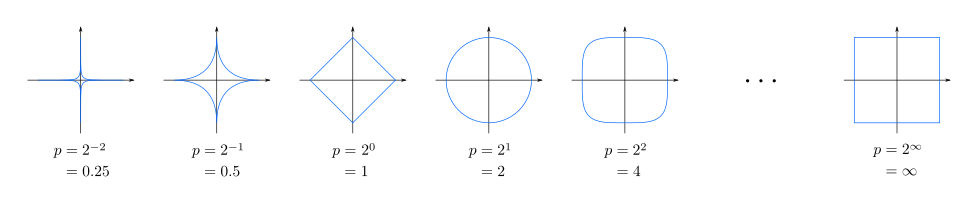Birim küre

Matematikte birim küre uzaklık kavramının iyi tanımlı olduğu bir kümenin adına merkez denilen belli bir noktasından sayıyla bir birim uzaklıkta yer alan ve yine aynı kümede yer alan noktaların kümesidir. Kapalı birim yuvar ise bir merkez noktasından bir birime eşit ve bir birimden daha az uzaklıktaki noktalar kümesidir. Açık birim yuvar ya da sadece birim yuvar denildiğinde ise merkez noktasından bir birimden daha az uzaklıktaki noktalar kümesi anlaşılır. Uzaklık kavramının tanımlı olduğu bu tür kümeler genellikle Öklid uzayları, ya da daha genel hâliyle metrik uzaylar ve normlu vektör uzaylarıdır.

Birim küre denildiğinde başnoktadan uzaklığı sayıyla bir olan noktaların kümesi anlaşılır ve uzlaşma aksi bir gösterim olmadıkça genellikle bu yöndedir. Merkezin başnokta olmadığı durumlarda birim kürenin merkezine vurgu yapılır. Uzaklığın bire eşit olmadığı durumlarda ise genel anlamda küre anlaşılır. Yani, birim küre, yarıçapın uzaklık kavramı üzerinden tanımlı olduğu ve bire eşit olduğu özel bir küredir.

Kapalı birim yuvar tanımı gereği birim küreyi altküme olarak içermektedir. Küredeki uzlaşmaya benzer şekilde, kapalı birim yuvar denilince, genellikle, başnoktadan uzaklığı bire eşit ya da birden küçük olan noktaların kümesi anlaşılır. Merkezin başnokta olmadığı durumlarda birim yuvarın merkezine vurgu yapılır. En genel haliyle, yarıçapın uzaklık kavramı üzerinden tanımlı olduğu ve birden küçük veya bire eşit olduğu özel kümelere kapalı birim yuvar denilir. Benzer uzlaşmalar açık birim yuvar için de geçerlidir.

${\displaystyle n}$ boyutlu Öklid uzayında birim küre

${\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}=1}$

denklemini sağlayan ${\displaystyle (x_{1},\ldots ,x_{n})}$ noktalarının kümesidir. Yine, aynı uzayda, kapalı birim yuvar

${\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}\leq 1}$

eşitsizliğini sağlayan ${\displaystyle (x_{1},\ldots ,x_{n})}$ noktalarının kümesidir.

Kapalı birim yuvarın birim küreden küme olarak farkı açık birim yuvarı verir. Diğer deyişle, ${\displaystyle n}$ boyutlu Öklid uzayında

${\displaystyle x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}<1}$

eşitsizliğini sağlayan ${\displaystyle (x_{1},\ldots ,x_{n})}$ noktalarının kümesine açık birim yuvar denilir.

Yarıçapı 1 birim olan ve x-, y- ve z- eksenlerinde değişikliğe sahip olmayan elipsoid birim kürenin klasik denklemini verir.

${\displaystyle f(x,y,z)=x^{2}+y^{2}+z^{2}=1}$

${\displaystyle n}$ boyutlu Öklid uzayında bir birim kürenin hacmi ve birim kürenin yüzey alanı birçok önemli formülde karşımıza çıkabilir.n boyutlu bir kürenin hacmini V_n olarak gösteririz, bu gama fonksiyonu kullanarak açıklanabilir.

${\displaystyle V_{n}={\frac {\pi ^{n/2}{\Gamma (1+n/2)}={\begin{cases}{\pi ^{n/2}/{(n/2)!}&\mathrm {if~} n\geq 0\mathrm {~is~even,} \\~\\{\pi ^{\lfloor n/2\rfloor }2^{\lceil n/2\rceil }/{n!!}&\mathrm {if~} n\geq 0\mathrm {~is~odd,} \end{cases}$

n!! double faktöriyel demektir. (n-1) boyutlu birim kürenin hiperhacmi (n boyutta bir yuvarın yüzey alanı gibi) A_n ile gösterilir ve alttaki formülle açıklanabilr;

${\displaystyle A_{n}=nV_{n}={\frac {n\pi ^{n/2}{\Gamma (1+n/2)}={\frac {2\pi ^{n/2}{\Gamma (n/2)}\,,}$

Son eşitlikte n > 0 olan değerler için kullanılabilr. Bazı ${\displaystyle n}$ değerleri için bazı yüzey alanlar ve hacimleri;

${\displaystyle n}$	${\displaystyle A_{n}$ (yüzey alan)		${\displaystyle V_{n}$ (hacim)
0	${\displaystyle 0(1/0!)\pi ^{0}$	0	${\displaystyle (1/0!)\pi ^{0}$	1
1	${\displaystyle 1(2^{1}/1!!)\pi ^{0}$	2	${\displaystyle (2^{1}/1!!)\pi ^{0}$	2
2	${\displaystyle 2(1/1!)\pi ^{1}=2\pi }$	6.283	${\displaystyle (1/1!)\pi ^{1}=\pi }$	3.141
3	${\displaystyle 3(2^{2}/3!!)\pi ^{1}=4\pi }$	12.57	${\displaystyle (2^{2}/3!!)\pi ^{1}=(4/3)\pi }$	4.189
4	${\displaystyle 4(1/2!)\pi ^{2}=2\pi ^{2}$	19.74	${\displaystyle (1/2!)\pi ^{2}=(1/2)\pi ^{2}$	4.935
5	${\displaystyle 5(2^{3}/5!!)\pi ^{2}=(8/3)\pi ^{2}$	26.32	${\displaystyle (2^{3}/5!!)\pi ^{2}=(8/15)\pi ^{2}$	5.264
6	${\displaystyle 6(1/3!)\pi ^{3}=\pi ^{3}$	31.01	${\displaystyle (1/3!)\pi ^{3}=(1/6)\pi ^{3}$	5.168
7	${\displaystyle 7(2^{4}/7!!)\pi ^{3}=(16/15)\pi ^{3}$	33.07	${\displaystyle (2^{4}/7!!)\pi ^{3}=(16/105)\pi ^{3}$	4.725
8	${\displaystyle 8(1/4!)\pi ^{4}=(1/3)\pi ^{4}$	32.47	${\displaystyle (1/4!)\pi ^{4}=(1/24)\pi ^{4}$	4.059
9	${\displaystyle 9(2^{5}/9!!)\pi ^{4}=(32/105)\pi ^{4}$	29.69	${\displaystyle (2^{5}/9!!)\pi ^{4}=(32/945)\pi ^{4}$	3.299
10	${\displaystyle 10(1/5!)\pi ^{5}=(1/12)\pi ^{5}$	25.50	${\displaystyle (1/5!)\pi ^{5}=(1/120)\pi ^{5}$	2.550

n ≥ 2 için genişletilmiş ondalık değerleri hassas olarak yuvarlanır.

A_n değerleri tekrarlamayı karşılar,

${\displaystyle A_{0}=0}$

${\displaystyle A_{1}=2}$

${\displaystyle A_{2}=2\pi }$

${\displaystyle A_{n}={\frac {2\pi }{n-2}A_{n-2}$ for ${\displaystyle n>2}$.

V_n değerleri tekrarlamayı karşılar,

${\displaystyle V_{0}=1}$

${\displaystyle V_{1}=2}$

${\displaystyle V_{n}={\frac {2\pi }{n}V_{n-2}$ for ${\displaystyle n>1}$.

A_n ve V_n herhangi bir gerçek sayın ≥ 0, için hesaplanabilir. n 0 olmayan bir tam sayı olduğunda kürenin alanını veya yuvarın hacmini saklamak için uygun koşullar vardır.

Yarıçapı r olan (n–1) boyutlu bir kürenin yüzey alanı A_n rⁿ⁻¹ ve yarıçapı r olan n boyutlu bir yuvarın hacmi V_n rⁿ. For instance, the area is {Kayma|A =.Örneğin, yarıçapı r olan üç boyutlu yuvarın yüzey alanı A = 4π r²’dir.Yarıçapı r olan üç boyutlu bir yuvarın hacmi ise V = 4π r³ / 3 ‘dir.

Normlu bir ${\displaystyle (V,\|\cdot \|)}$ uzayında, açık birim yuvar

${\displaystyle \{x\in V:\|x\|<1\}$

kümesi olarak tanımlanır. Benzer bir şekilde, kapalı birim yuvar

${\displaystyle \{x\in V:\|x\|\leq 1\}$

kümesi olarak tanımlanır. Aynı uzayda, birim küre ise

${\displaystyle \{x\in V:\|x\|=1\}$

kümesi olarak tanımlanır.

Birim yuvarın şekli tamamen seçilen norma bağlıdır. İyi köşelere sahip olabilir ve [−1,1] gibi görülebilir ve norm ⁿ,durumunda l_∞ in Rⁿ. Normal yuvarlak bir yuvar genellikle Hilbert spacenormu üzerinde sonlu-boyutlu Öklid mesafesi üzerinde anlaşılır.Sınırladığı alan birim kürenin genellikle hangi anlama geldiğini tanımlar.p çeşitli değerlerinde, birim yuvarın iki boyutlu uzayı ℓ p {\displaystyle \ell ^{p} space için burada bazı fotoğraflar vardır.(birim yuvar konkav olduğunda p < 1,konveks olduğunda p ≥ 1):

Bu nedenle bu durump ≥ 1 göstermektedir. İki boyutlu birim yuvarların çevreleri${\displaystyle C_{p}$;

${\displaystyle C_{0}=C_{\infty }=8}$ maximum değerdir.

${\displaystyle C_{1}=4{\sqrt {2}$ minimum değerdir.

${\displaystyle C_{2}=2\pi \,.}$

Yukarıda tanımlanan her üç doğrudan, seçilen orijine göre bir metrik uzay açıkça genelleştirilebilir.Ancak, topolojik düşünceler(iç, kapatma, sınır) aynı yola (ultrametric alanlarda, açık kapalı kümelerin tümü)başvurmaya ihtiyaç duymaz ve birim küre bazı metrik uzaylarda boş bile olabilir.

Eğer V gerçek olan bir doğrusal uzayın kuadratik form’u F:V → R, daha sonra { p ∈ V : F(p) = 1 } birim küre ya da Vnin birim yarı küresidir denebilir.Örneğin;kuadrik formu ${\displaystyle x^{2}-y^{2}$,,birine eşit ayarlandığında bölünmüş karmaşık sayılar düzleminde birim çember rolünü oynayan birim hiperbol oluşturulur.Kuadratik formu x² uzayın içinde birim küre için bir çizgi çifti oluşturur.