Mäydan
Bu turıpoçmaqnıñ mäydanı = lw Mäydan - geometrik ike ülçäneşle figura (yassı yä käkre) san sıyfatlaması, figuranıñ zurlığın kürsätä.
Tarixında mäydan xisaplaw kvadratura dip yörtelä.
Mäydanğa iä buluçı figura - kvadraturalı dip isemlänä.
İntegral' isäpläw geometrik figuralarnı ğomumi xisaplaw ısulın birä.
Uñaylıq Additivlek - figuranıñ mäydanı eçke figuranıñ öleşläre summasına tigezİnvariantlıq - kongruent figuralarınıñ mäydannarı bertigezNormalaştırlıq - ber-yaqlı kvadrat mäydanı bergä tigez.
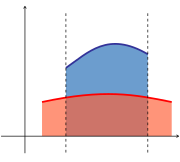
Bilgelängän İntegral - figura mäydanı İke fuktsiä sızıqları arasındağı mäydan - integrallar ayırmasına tigez Funktsiä grafigı häm gorizontal' küçär arasında mäydan
[
a
,
b
]
{\displaystyle [a,b]}
S
=
∫
a
b
f
(
x
)
d
x
{\displaystyle S=\int \limits _{a}^{b}f(x)\,dx}
İke funktsiä grafigı arasında mäydan:
S
=
∫
a
b
|
f
(
x
)
−
g
(
x
)
|
d
x
{\displaystyle S=\int \limits _{a}^{b}\left|f(x)-g(x)\right|\,dx}
Polär koordinatlarda mäydan:
S
=
1
2
∫
θ
1
θ
2
r
2
(
θ
)
d
θ
{\displaystyle S={1 \over 2}\int \limits _{\theta _{1}^{\theta _{2}r^{2}(\theta )\,d\theta }
S
=
∬
A
|
∂
r
∂
u
×
∂
r
∂
v
|
d
u
d
v
.
{\displaystyle S=\iint \limits _{A}\left|{\frac {\partial \mathbf {r} }{\partial u}\times {\frac {\partial \mathbf {r} }{\partial v}\right|\,du\,dv.}
yäki tulı koordinatlarda
S
=
∬
A
(
D
(
x
,
y
)
D
(
u
,
v
)
)
2
+
(
D
(
y
,
z
)
D
(
u
,
v
)
)
2
+
(
D
(
z
,
x
)
D
(
u
,
v
)
)
2
d
u
d
v
{\displaystyle S=\iint \limits _{A}{\sqrt {\left({\frac {D(x,y)}{D(u,v)}\right)^{2}+\left({\frac {D(y,z)}{D(u,v)}\right)^{2}+\left({\frac {D(z,x)}{D(u,v)}\right)^{2}\;\mathrm {d} \,u\,\mathrm {d} \,v}
biredä
D
(
y
,
z
)
D
(
u
,
v
)
=
|
y
u
′
y
v
′
z
u
′
z
v
′
|
,
D
(
z
,
x
)
D
(
u
,
v
)
=
|
z
u
′
z
v
′
x
u
′
x
v
′
|
,
D
(
x
,
y
)
D
(
u
,
v
)
=
|
x
u
′
x
v
′
y
u
′
y
v
′
|
{\displaystyle {\frac {D(y,z)}{D(u,v)}={\begin{vmatrix}y'_{u}&y'_{v}\\z'_{u}&z'_{v}\end{vmatrix},\quad {\frac {D(z,x)}{D(u,v)}={\begin{vmatrix}z'_{u}&z'_{v}\\x'_{u}&x'_{v}\end{vmatrix},\quad {\frac {D(x,y)}{D(u,v)}={\begin{vmatrix}x'_{u}&x'_{v}\\y'_{u}&y'_{v}\end{vmatrix}
Kvadrat kilometr 1 km² = 1 000 000 m²Gektar 1 ga = 10 000 m²Ar 1 a = 100 m²
Энциклопедия элементарной математики. Книга пятая. Геометрия / под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М.: Наука, 1966. — 624 с.
Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2
История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. I: С древнейших времён до начала Нового времени.
История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. II: Математика XVII столетия.
Boyer C. B., Merzbach U. C. A History of Mathematics. — John Wiley & Sons, 2010. — 640 p
The article is a derivative under the Creative Commons Attribution-ShareAlike License .
A link to the original article can be found here and attribution parties here
By using this site, you agree to the Terms of Use . Gpedia ® is a registered trademark of the Cyberajah Pty Ltd


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





