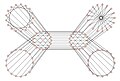
Граф Бігса — Сміта
| Граф Бігса–Сміта | |
|---|---|
 Граф Бігса–Сміта | |
| Вершин | 102 |
| Ребер | 153 |
| Радіус | 7 |
| Діаметр | 7 |
| Обхват | 9 |
| Автоморфізм | 2448 (PSL(2,17)) |
| Хроматичне число | 3 |
| Хроматичний індекс | 3 |
| Властивості | Кубічний граф Симетричний граф Гамільтонів граф дистанційно-регулярний граф |
Граф Біґґза–Сміта — 3-регулярний граф зі 102 вершинами і 153 ребрами. Хроматичне число графа дорівнює 3, хроматичний індекс дорівнює 3, радіус дорівнює 7, діаметр — 7, а обхват — 9. Граф є також вершинно 3-зв'язним і реберно 3-зв'язним.
Всі кубічні дистанційно-регулярні графи відомі[1], граф Бігса — Сміта — один з 13-ти таких графів.
Алгебричні властивості
Група автоморфізмів графа Бігса — Сміта — це група порядку 2448[2], ізоморфна група проєктивної групи PSL(2,17). Вона діє транзитивно на вершини і ребра графа, тому граф Бігса — Сміта є симетричним. Граф має автоморфізм, який переводить будь-яку вершину в будь-яку іншу і будь-яке ребро в будь-яке інше ребро. У списку Фостера граф Бігса — Сміта, зазначений як F102A і є єдиним симетричним графом зі 102 вершинами[3].
Граф Бігса — Сміта однозначно визначається за його спектром, множиною власних значень та матрицею суміжності графа[4].
Характеристичний многочлен графа Бігса — Сміта дорівнює:
- .
Галерея
-
Хроматичне число графа Бігса — Сміта дорівнює 3.
-
Хроматичний індекс графа Бігса — Сміта дорівнює 3.
-
Альтернативне графічне подання графа Бігса — Сміта.
-
Розклад графа Бігса — Сміта на 6 множин по 17 елементів у кожній.
Примітки
- ↑ AE Brouwer, AM Cohen, A. Neumaier. Distance-Regular Graphs. — New York : Springer-Verlag, 1989.
- ↑ Royle, G. F102A data[недоступне посилання з квітня 2019]
- ↑ M. Conder, P. Dobcsányi, «Trivalent Symmetric Graphs Up to 768 Vertices.» J. Combin. Math. Combin. Comput. 40, 41-63, 2 002.
- ↑ E. R. van Dam and WH Haemers, Spectral Characterizations of Some Distance-Regular Graphs. J. Algebraic Combin. 15, pages 189—202, 2003
Джерела
- On trivalent graphs, NL Biggs, DH Smith — Bulletin of the London Mathematical Society, 3 (1971) 155—158.