哈代-李特爾伍德第一猜想

First Hardy–Littlewood conjecture

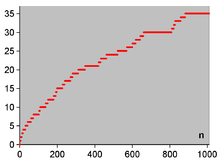小於給定的${\displaystyle n}$的孿生質數的數量的圖。哈代-李特爾伍德第一猜想預測說會有無限多對這樣的數。
領域	數論
猜想提出者	G·H·哈代 約翰·恩瑟·李特爾伍德
猜想提出年	1923
開放問題	是

在數論中，哈代-李特爾伍德第一猜想（first Hardy–Littlewood conjecture）^[1]指的是對小於給定數的質數k元組（英语：Prime_k-tuple）的非病態公式，這猜想是對質數定理的推廣。這猜想最初由G·H·哈代和約翰·恩瑟·李特爾伍德在1923年提出。^[2]

設${\displaystyle m_{1},m_{2},\ldots ,m_{k}$為一組使得${\displaystyle P=(p,p+m_{1},p+m_{2},\ldots ,p+m_{k})}$不對任何質數構成一個完全剩餘系的正整數，並以${\displaystyle \pi _{P}(n)}$表示不大於${\displaystyle n}$並使得${\displaystyle p+m_{1},p+m_{2},\ldots ,p+m_{k}$皆為質數的質數${\displaystyle p}$的數量，那麼有：^[1][3]

${\displaystyle \pi _{P}(n)\sim C_{P}\int _{2}^{n}{\frac {dt}{\log ^{k+1}t},}$

其中

${\displaystyle C_{P}=2^{k}\prod _{q{\text{ prime,} \atop q\geq 3}{\frac {1-{\frac {w(q;m_{1},m_{2},\ldots ,m_{k})}{q}{\left(1-{\frac {1}{q}\right)^{k+1}$

是奇質數的乘積，且此處${\displaystyle w(q;m_{1},m_{2},\ldots ,m_{k})}$表示${\displaystyle 0,m_{1},m_{2},\ldots ,m_{k}$除以${\displaystyle q}$後，其中不同的餘數的個數。

${\displaystyle k=1}$且${\displaystyle m_{1}=2}$的情況和孿生質數猜想相關，特別地，若以${\displaystyle \pi _{2}(n)}$表示不大於${\displaystyle n}$的孿生質數個數，那麼有

${\displaystyle \pi _{2}(n)\sim C_{2}\int _{2}^{n}{\frac {dt}{\log ^{2}t},}$

其中

${\displaystyle C_{2}=2\prod _{\textstyle {q{\text{ prime,} \atop q\geq 3}\left(1-{\frac {1}{(q-1)^{2}\right)\approx 1.320323632\ldots }$

是孿生質數常數。^[3]

質數k元組的斯奎斯數，是根據哈代-李特爾伍德第一猜想，在質數k元組上對斯奎斯數的定義的推廣。質數k元組${\displaystyle P}$的斯奎斯數的定義是最小的違反哈代-李特爾伍德的質數${\displaystyle p}$，也就是最小的使得下式成立的質數：^[3]

${\displaystyle \pi _{P}(p)>C_{P}\operatorname {li} _{P}(p),}$

目前已證明說，哈代-李特爾伍德第一猜想和哈代-李特尔伍德第二猜想彼此不相容。^[4]

Bateman–Horn猜想（英语：Bateman–Horn conjecture）是哈代-李特爾伍德第一猜想在次數大於一的多項式上的推廣。^[1]

• Aletheia-Zomlefer, Soren Laing; Fukshansky, Lenny; Garcia, Stephan Ramon. The Bateman–Horn conjecture: Heuristic, history, and applications. Expositiones Mathematicae. 2020, 38 (4): 430–479. ISSN 0723-0869. doi:10.1016/j.exmath.2019.04.005 . 
• Tóth, László. On the Asymptotic Density of Prime k-tuples and a Conjecture of Hardy and Littlewood. Computational Methods in Science and Technology. January 2019, 25 (3): 143–138. arXiv:1910.02636 . doi:10.12921/cmst.2019.0000033.