在數學 及经典力學 中,泊松括號 是哈密顿力學 中重要的運算,在哈密頓表述的動力系統 中時間演化的定義起着中心角色。在更一般的情形,泊松括号用来定义一个泊松代数 ,而泊松流形 是一个特例。它们都是以西莫恩·德尼·泊松 命名的。
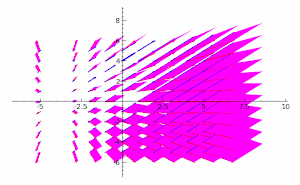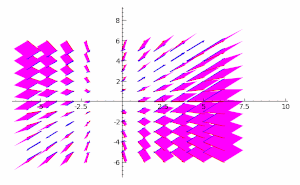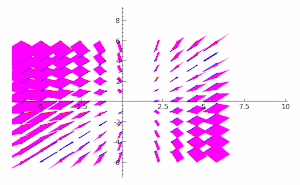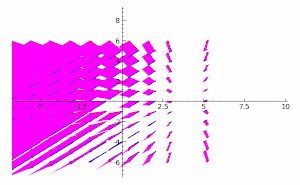
取决于时间的向量场演示图。泊松括号是用这个向量场的分量函数定义的。 两个取决于时间的向量场演示图,表示了上一个向量场分量的梯度函数。 两个取决于时间的向量场的叉积示意图,表示了原向量场分量的梯度函数。两个函数的括号是它们的pq-梯度的叉积的长度。这说明了括号、梯度 与叉积 的关系;由无穷小梯度向量组成的平行四边形 越大,括号越大。
在正則坐標
(
q
i
,
p
j
)
{\displaystyle (q_{i},p_{j})}
相空间 内两个函数
f
(
q
,
p
)
,
g
(
q
,
p
)
{\displaystyle f(\mathbf {q} ,\ \mathbf {p} ),\ g(\mathbf {q} ,\ \mathbf {p} )}
泊松括號 具有如下形式:
{
f
,
g
}
=
∑
i
=
1
N
[
∂
f
∂
q
i
∂
g
∂
p
i
−
∂
f
∂
p
i
∂
g
∂
q
i
]
{\displaystyle \{f,g\}=\sum _{i=1}^{N}\left[{\frac {\partial f}{\partial q_{i}{\frac {\partial g}{\partial p_{i}-{\frac {\partial f}{\partial p_{i}{\frac {\partial g}{\partial q_{i}\right]}
哈密顿-雅可比运动方程 有一个使用泊松括号的等价表示。这可最直接地用坐标系表示。假设
f
(
p
,
q
,
t
)
{\displaystyle f(p,q,t)}
d
d
t
f
(
p
,
q
,
t
)
=
∂
f
∂
t
+
∂
f
∂
p
d
p
d
t
+
∂
f
∂
q
d
q
d
t
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}f(p,q,t)={\frac {\partial f}{\partial t}+{\frac {\partial f}{\partial p}{\frac {\mathrm {d} p}{\mathrm {d} t}+{\frac {\partial f}{\partial q}{\frac {\mathrm {d} q}{\mathrm {d} t}
然后,取
p
=
p
(
t
)
{\displaystyle p=p(t)}
q
=
q
(
t
)
{\displaystyle q=q(t)}
q
˙
=
∂
H
/
∂
p
{\displaystyle {\dot {q}={\partial H}/{\partial p}
p
˙
=
−
∂
H
/
∂
q
{\displaystyle {\dot {p}=-{\partial H}/{\partial q}
d
d
t
f
(
p
,
q
,
t
)
=
∂
f
∂
t
+
∂
f
∂
q
∂
H
∂
p
−
∂
f
∂
p
∂
H
∂
q
=
∂
f
∂
t
+
{
f
,
H
}
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}f(p,q,t)={\frac {\partial f}{\partial t}+{\frac {\partial f}{\partial q}{\frac {\partial H}{\partial p}-{\frac {\partial f}{\partial p}{\frac {\partial H}{\partial q}={\frac {\partial f}{\partial t}+\{f,H\}
从而,辛流形上一个函数f 的演化可用辛同胚 单参数族 给出,以时间t 为参数。丢掉坐标系,我们有
d
d
t
f
=
(
∂
∂
t
−
{
H
,
⋅
}
)
f
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}f=\left({\frac {\partial }{\partial t}-\{\,H,\cdot \,\}\right)f}
算子
−
{
H
,
⋅
}
{\displaystyle -\{\,H,\cdot \,\}
刘维尔算子 。
一个可积动力系统可能有能量以外的运动常数 。这样的运动常数在泊松括号下将与哈密顿量 交换。假设某个函数
f
(
p
,
q
)
{\displaystyle f(p,q)}
p
(
t
)
,
q
(
t
)
{\displaystyle p(t),q(t)}
哈密顿运动方程 的一条轨迹 或解,则沿着轨迹有
0
=
d
f
d
t
{\displaystyle 0={\frac {\mathrm {d} f}{\mathrm {d} t}
0
=
d
d
t
f
(
p
,
q
)
=
∂
f
∂
p
d
p
d
t
+
∂
f
∂
q
d
q
d
t
=
∂
f
∂
q
∂
H
∂
p
−
∂
f
∂
p
∂
H
∂
q
=
{
f
,
H
}
{\displaystyle 0={\frac {\mathrm {d} }{\mathrm {d} t}f(p,q)={\frac {\partial f}{\partial p}{\frac {\mathrm {d} p}{\mathrm {d} t}+{\frac {\partial f}{\partial q}{\frac {\mathrm {d} q}{\mathrm {d} t}={\frac {\partial f}{\partial q}{\frac {\partial H}{\partial p}-{\frac {\partial f}{\partial p}{\frac {\partial H}{\partial q}=\{f,H\}
这里中间步骤利用运动方程得到。这个方程称为刘维尔方程 。刘维尔定理 描述了如上给出的一个测度 (或相空间上分布函数 )的时间演化。
为了使一个哈密顿系统完全可积,所有的运动常数必须互相对合。
設M 是一個辛流形 ,即流形 上帶有一個辛形式 (闭 的非退化2-形式 ):
ω
{\displaystyle \omega }
d
ω
=
0
{\displaystyle d\omega =0}
ω
:
ξ
∈
v
e
c
t
[
M
]
→
i
ξ
ω
∈
Λ
1
[
M
]
{\displaystyle \omega :\xi \in \mathrm {vect} [M]\rightarrow i_{\xi }\omega \in \Lambda ^{1}[M]}
ω
{\displaystyle \omega }
ω
~
:
Λ
1
[
M
]
→
v
e
c
t
[
M
]
{\displaystyle {\tilde {\omega }:\Lambda ^{1}[M]\rightarrow \mathrm {vect} [M]}
d
{\displaystyle d}
M 上内蕴的外导数 运算,而
i
ξ
θ
{\displaystyle i_{\xi }\theta }
内乘 或缩并运算,在1-形式
θ
{\displaystyle \theta }
θ
(
ξ
)
{\displaystyle \theta (\xi )}
由外微分 的公理,我们由:
i
[
v
,
w
]
ω
=
d
(
i
v
i
w
ω
)
+
i
v
d
(
i
w
ω
)
−
i
w
d
(
i
v
ω
)
−
i
w
i
v
d
ω
,
{\displaystyle i_{[v,w]}\omega =d(i_{v}i_{w}\omega )+i_{v}d(i_{w}\omega )-i_{w}d(i_{v}\omega )-i_{w}i_{v}d\omega ,\,}
这里
[
v
,
w
]
{\displaystyle [v,w]}
李括号 ,其性质本质上定义了M 上流形结构。
如果v 使得
d
(
i
v
ω
)
=
0
{\displaystyle d(i_{v}\omega )=0}
ω
{\displaystyle \omega }
余闭 )。类似地,如果
i
v
ω
=
d
f
{\displaystyle i_{v}\omega =df}
f 成立,我们称v
ω
{\displaystyle \omega }
余恰当 )。已知
d
ω
=
0
{\displaystyle d\omega =0}
v 和w 都余闭时,表达式中惟一非零项是
d
(
i
v
i
w
ω
)
{\displaystyle d(i_{v}i_{w}\omega )}
d
∘
d
=
0
{\displaystyle d\circ d=0}
抽象代数 的话来说,余闭向量场组成了M 上光滑向量场李代数 的一个子代数,而余恰当向量场组成这个子代数的一个代数理想 。
假设存在逆映射
ω
~
{\displaystyle {\tilde {\omega }
M 上每个光滑实值函数f 可以与一个余恰当向量场相伴
ω
~
(
d
f
)
{\displaystyle {\tilde {\omega }(df)}
d 的核,即在M 的任何连通分支上是常数)。这样我们定义
(
M
,
ω
)
{\displaystyle (M,\omega )}
泊松括号 ,为可微 函数 上一个双线性 运算,在泊松括号下
C
∞
{\displaystyle C^{\infty }
代数 。它由下式给出:
{
f
,
g
}
=
i
ω
~
(
d
f
)
d
g
=
−
i
ω
~
(
d
g
)
d
f
=
−
{
g
,
f
}
{\displaystyle \{f,g\}=i_{\tilde {\omega }(df)}dg=-i_{\tilde {\omega }(dg)}df=-\{g,f\}\,}
泊松括号的反对称性由外导数 的公理与条件
d
ω
{\displaystyle d\omega }
ω
~
{\displaystyle {\tilde {\omega }
泊松双向量 或泊松结构 ,泊松括号简单地写做
{
f
,
g
}
=
ω
~
(
d
f
,
d
g
)
{\displaystyle \{f,g\}={\tilde {\omega }(df,dg)}
光滑函数上的泊松括号对应于余恰当向量场上的李括号并继承了它的性质。从而它满足雅可比恒等式 :
{
f
,
{
g
,
h
}
}
+
{
g
,
{
h
,
f
}
}
+
{
h
,
{
f
,
g
}
}
=
0
{\displaystyle \{f,\{g,h\}\}+\{g,\{h,f\}\}+\{h,\{f,g\}\}=0\,}
关于一个特定的数量场f 的泊松括号
{
f
,
_
}
{\displaystyle \{f,\_\}
ω
~
(
d
f
)
{\displaystyle {\tilde {\omega }(df)}
李导数 。从而,它是一个导子 ,即它满足莱布尼兹法则 :
{
f
,
g
h
}
=
{
f
,
g
}
h
+
g
{
f
,
h
}
{\displaystyle \{f,gh\}=\{f,g\}h+g\{f,h\}\,}
这是流形的一个基本性质,关于两个向量场的李导数运算的交换子 等价于关于某个向量场的李导数,即它们的李括号。泊松括号中平行的脚色显然是雅可比恒等式的一个变形:
{
f
,
{
g
,
h
}
}
−
{
g
,
{
f
,
h
}
}
=
{
{
f
,
g
}
,
h
}
{\displaystyle \{f,\{g,h\}\}-\{g,\{f,h\}\}=\{\{f,g\},h\}\,}
如果f 和g 的泊松括号消失(
{
f
,
g
}
=
0
{\displaystyle \{f,g\}=0}
f 与g 称为互相对合 (mutual involution ),并有关于f 和g 取泊松括号的运算交换。
泊松括號 是反交换的 ,也滿足雅可比恒等式 。这使得辛流形 上的光滑函数 空间成为無限維的李代數 ,以泊松括號为李括號 。相应的李群 是辛流形的辛同胚 群(也稱為正則變換 )。
给定一个可微切丛 上的向量场 X ,令
P
X
{\displaystyle P_{X}
共轭动量 。这个从场到共轭动量的映射为从泊松括號到李括號 的李代數 反同态:
{
P
X
,
P
Y
}
=
−
P
[
X
,
Y
]
{\displaystyle \{P_{X},P_{Y}\}=-P_{[X,Y]}\,}
这个重要结果值得我们给个简短证明。记位形空间 的q 点的向量场X 为
X
q
=
∑
i
X
i
(
q
)
∂
∂
q
i
{\displaystyle X_{q}=\sum _{i}X^{i}(q){\frac {\partial }{\partial q^{i}
其中
∂
/
∂
q
i
{\displaystyle \partial /\partial q^{i}
X 的共轭动量的表达式为
P
X
(
q
,
p
)
=
∑
i
X
i
(
q
)
p
i
{\displaystyle P_{X}(q,p)=\sum _{i}X^{i}(q)\;p_{i}
这里
p
i
{\displaystyle p_{i}
相空间 的每点
(
q
,
p
)
{\displaystyle (q,p)}
{
P
X
,
P
Y
}
(
q
,
p
)
=
∑
i
∑
j
{
X
i
(
q
)
p
i
,
Y
j
(
q
)
p
j
}
{\displaystyle \{P_{X},P_{Y}\}(q,p)=\sum _{i}\sum _{j}\{X^{i}(q)\;p_{i},Y^{j}(q)\;p_{j}\}
=
∑
i
j
p
i
Y
j
(
q
)
∂
X
i
∂
q
j
−
p
j
X
i
(
q
)
∂
Y
j
∂
q
i
{\displaystyle =\sum _{ij}p_{i}Y^{j}(q){\frac {\partial X^{i}{\partial q^{j}-p_{j}X^{i}(q){\frac {\partial Y^{j}{\partial q^{i}
=
−
∑
i
p
i
[
X
,
Y
]
i
(
q
)
{\displaystyle =-\sum _{i}p_{i}\;[X,Y]^{i}(q)}
=
−
P
[
X
,
Y
]
(
q
,
p
)
{\displaystyle =-P_{[X,Y]}(q,p)\,}
以上对所有
(
q
,
p
)
{\displaystyle (q,p)}




![{\displaystyle \{f,g\}=\sum _{i=1}^{N}\left[{\frac {\partial f}{\partial q_{i}{\frac {\partial g}{\partial p_{i}-{\frac {\partial f}{\partial p_{i}{\frac {\partial g}{\partial q_{i}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4e1386230b0a90463e2e87a987699b9c42fcbb1)















![{\displaystyle \omega :\xi \in \mathrm {vect} [M]\rightarrow i_{\xi }\omega \in \Lambda ^{1}[M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98992ceecc54b501a1f1e2bcf9ff2dbc14d80da6)
![{\displaystyle {\tilde {\omega }:\Lambda ^{1}[M]\rightarrow \mathrm {vect} [M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f76197c75253f15e76500fd61d7f7ceed9ab879)




![{\displaystyle i_{[v,w]}\omega =d(i_{v}i_{w}\omega )+i_{v}d(i_{w}\omega )-i_{w}d(i_{v}\omega )-i_{w}i_{v}d\omega ,\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42075304d8533c6321397172da0aaaa8737b7022)
![{\displaystyle [v,w]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81599dd26b00c77086bda71448f9011328e690f1)

















![{\displaystyle \{P_{X},P_{Y}\}=-P_{[X,Y]}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9fd6a609dcfbb894df45602b56345e90151d478)







![{\displaystyle =-\sum _{i}p_{i}\;[X,Y]^{i}(q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604325784f517d88a8dbdc3c6c16c6bf6cbe461d)
![{\displaystyle =-P_{[X,Y]}(q,p)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a40987db396ad06f228de74295360335b1a3cc6)