在數學裡,有著許多明顯矛盾的虛假證明存在。即使其證明是有缺陷的,其錯誤——通常是經過設計的——卻常是較難抓摸的。這些謬誤一般都儘止於好奇而已,但可以被用来顯示嚴謹在數學中的重要性。
大多數此類的證明都仰賴著同種錯誤的變形 此一錯誤為採一非單射的函數 ,以觀察對某些
,以觀察對某些 和
和 ,會有
,會有 ,來(錯誤地)做出
,來(錯誤地)做出 的結論。零除數是此類錯誤的一特例;
的結論。零除數是此類錯誤的一特例; 為將
為將 映射至
映射至 的函數,而其錯誤的一步是起於將
的函數,而其錯誤的一步是起於將 的等式做成
的等式做成 的結論。相似地,下面證明了
的結論。相似地,下面證明了 的句子也是以函數
的句子也是以函數 的同一種錯誤造成的。其錯誤的一步始於有某個
的同一種錯誤造成的。其錯誤的一步始於有某個 和
和 會使得
會使得 的一正確申論,然後做出了
的一正確申論,然後做出了 的一錯誤結論。
的一錯誤結論。
算术例子
證明1是最大的正整數
- 假設最大的正整數不是
 ,而是
,而是 ,有
,有 ;
;
 ,
, 為正的,所以由
為正的,所以由 得到
得到 ;
;
- 但是
 還是正整數,可是沒有任何正整數比
還是正整數,可是沒有任何正整數比 大,矛盾;
大,矛盾;
Q.E.D.
此一證明是無效的,因為最大的正整數不存在,因此不能如此假設。
證明-1等於1
- 由一等式開始

- 將兩邊轉成假分數

- 將兩邊開方

- 其會等於

- 兩邊同乘
 以來消去分數
以來消去分數

- 但任一數的開方之平方會給出原本的數來,故

Q.E.D.
此一證明是無效的,因為負數的開方不是实数, 推出
推出 是错误的(事實上,
是错误的(事實上, ,
, )。
)。
證明1等於2
1.令 ,且
,且
2.將兩邊乘以a

3.將兩邊減掉

4.將兩邊因式分解

5.將兩邊除以

6.因為 因此
因此

7.簡化

8.將兩邊除以b

Q.E.D.
這個證明的錯誤點在於第五步, 正因為a=b所以a-b等於零,而除以零是無效的。
正因為a=b所以a-b等於零,而除以零是無效的。
證明4等於5
- 由一等式開始

- 將等式兩邊以稍微不同但相等的方式表示

- 將兩邊做因式分解

- 將兩邊加上相同的數

- 將兩邊再做一次因式分解

- 將兩邊開方

- 消去相同的項

Q.E.D.
那一證明內的錯誤在於 不表示
不表示 的這一事實。到此之前的算術都是正確的,而事實上,
的這一事實。到此之前的算術都是正確的,而事實上, 。需注意的是,若將4減去
。需注意的是,若將4減去 ,會得到
,會得到 。若再平方的話,則會得到正的
。若再平方的話,則會得到正的 。其下一個邏輯的數學步驟為取兩邊的平方。若這樣做的話,則將會看見
。其下一個邏輯的數學步驟為取兩邊的平方。若這樣做的話,則將會看見 會等於
會等於 。原始的
。原始的 式子事實上是會導致一個正確的等式的(若此一問題是以此一純粹的方式運算的話)。
式子事實上是會導致一個正確的等式的(若此一問題是以此一純粹的方式運算的話)。
證明1+1=0
- 求
 ︰
︰

Q.E.D.
此證明的錯誤在於 只有在a與b不皆為負數才成立,
只有在a與b不皆為負數才成立, 並不等於
並不等於 。
。
證明0=1
首先,設定一個無窮級數。

因為 ,因此:
,因此:

拆括號之後在於不同的地方加上括號:

 ,因此:
,因此:


Q.E.D.
這個證明的錯誤在於,無窮等比級數在公比的絕對值大於等於一的情況下,將括號插入無窮級數求無窮和是沒有意義的,因為這樣的無窮等比級數和發散。因此這類條件不適用於格蘭迪級數  。
。
證明任何數字等於1/任何數字






Q.E.D.
這個證明的錯誤在於, 不等於
不等於  ,正確等式應是
,正確等式應是 (下一步:
(下一步: )。
)。
證明0/0等於0
首先,我們知道:


由於
因此
因此
Q.E.D.
這個證明的錯誤在於, 成立的前提有
成立的前提有 。
。
證明任意兩數都是相等的
設
設
由和立方與差立方公式可知:


由於


將 代入
代入 ,可得:
,可得:

因此:

代入 ,可得:
,可得:

Q.E.D.
这个证明的错误在于:
1、在以上的假设下,可得 ,所以
,所以 和
和 并不是独立的;
并不是独立的;
2、在复数域中,由 得不出
得不出 。在此证明中,由
。在此证明中,由 得出
得出 是错误的。
是错误的。
几何例子
第一题:证明任何三角形都是正三角形
 第一题错误的证图
第一题错误的证图
 第一题正确的证图
第一题正确的证图
 第二题错误的证图
第二题错误的证图
 第二题正确的证图
第二题正确的证图
给定三角形△ABC,证明AB = AC:
- 作∠A的角平分线。
- 作BC的垂直平分线,并设BC的中点为D。
- 设这两条直线的交点为P。
- 从P向AB和AC作垂线,并设垂足为E和F。
- 作直线PB和PC。
- △EAP ≅ △FAP(AP = AP;∠PAF ≅ ∠PAE由于AP平分∠A;∠AEP ≅ ∠AFP都是直角)。
- △PDB ≅ △PDC(∠PDB、∠PDC是直角;PD = PD;BD = CD由于PD平分BC)。
- △EPB ≅ △FPC(EP = FP由于△EAP ≅ △FAP;BP = CP由于△PDB ≅ △PDC;∠EPB ≅ ∠FPC由于它们是对顶角)。
- 因此,AE ≅ AF,EB ≅ FC,AB = AE + EB = AF + FC = AC。
- 同理,AB = BC,AC = BC。
证毕。
这个证明的错误在于,只有在△ABC為等腰三角形,P才會位于三角形的内部,而且AP与DP会重合。
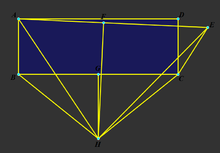
第二题:证明直角等于钝角
给定一个矩形ABCD,证明∠DCB=∠ECB;
- 在矩形ABCD外作CE=CD。
- 联结AE。
- 作BC、AE的中垂线,它们的垂足分别是G、F,两条直线交于H。
- 在中垂线上的点到线段两端的距离是相等的,所以HA=HE,HB=HC。
- 矩形的对边相等,得AB=DC;加上作图要求,得AB=EC。
- 利用S.S.S得△ABH≅△ECH。于是得∠ABH=∠ECH。
- 由于HB=HC,则得∠HBC=∠HCB。
- 等量减等量,得∠ABC=∠ECB。
- 矩形的四个角都是90°,得∠ABC=∠ECB=90°。
Q.E.D.
这个证明的错误在于,由于△ABH≅△ECH,则∠BHA=∠CHE,即∠AHE=∠BHC-∠BHA+∠CHE,可以把∠AHE看作是∠BHC的旋转,因AH穿过了矩形ABCD,则EH是不可能穿过矩形ABCD的。
微积分例子
证明0等于1
我们从计算以下的不定积分开始:

利用分部积分法,可得:
 ,
,
因此:
 ,
,
所以,有:



证毕。
这个证明的错误在于,忽略了積分完會出現的積分常數C。若繼續計算,會得到 。
。
參見












































































































