Индекс на Милър

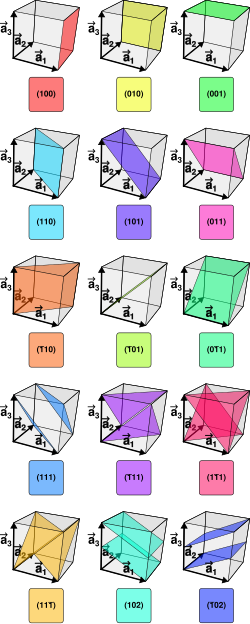
Кристалографският индекс на Милър е система за означаване на разположението на кристалните плоскости в пространството. Всяка кристална форма се състои от симетрично разположени еквивалентни стени, съответстващи на атомни мрежи в триизмерната пространствена решетка, която от своя страна се определя най-общо чрез елементарна клетка с ребра и междуребрени ъгли. Индексът на Милър представлява група от цифри, определящи разположението на атомните плоскости и еквивалентните стени в кристалната решетка по отношение на избрана координатна система, която не винаги е декартова. В частност положението на плоскостите на кристалната решетка се определят от три цели числа, приети условно като h, k и l, затворени в кръгли скоби (hkl) и наречени индекс на Милър – например (001) (110) (102). Ориентацията на тези плоскости може да бъде определена чрез координатите на точките, в които те се пресичат с основните кристалографски оси на твърдото тяло.^[1][2]

• Записани в кръгли скоби (hkl) означават индекс на Милър за единична плоскост от кристалната решетка.
• Записани в големи скоби {hkl} означават индекс на Милър за съвкупността от всички равностойни плоскости на кристалната решетка, успоредни една на друга, т.е. изразява простата кристалографска форма.
• Записани в квадратни скоби [hkl] характеризират направлението на ребрата, съответстващи на атомните редици в кристалната структура. Изразяват посоката на вектора на тези ребра и са изчислени на базата на обикновени, а не реципрочни стойности. Трите числа, затворени в квадратни скоби се наричат индекс (параметри) на Вайс.^[3][4] Квадратни скоби се използват още и при обозначаване на ръбовете на кристалните форми.^[2][5]

Когато кристалната решетка се характеризира с четирираменен осен кръст (при тригонална и хексагонална сингония, моноклинни и триклинни кристали), индексът на Милър се изразява с четири цифри, затворени в кръгли скоби – съответно за стена и проста кристалографска форма, например (0001).^[6] При тях първите три оси не са самостоятелни, а взаимно свързани, а оттук това се отнася и до първите три цифри в индекса.^[3]

Индексът на Милър е въведен през 1839 г. от британския минералог и кристалограф Уилям Халоус Милър.^[7]

Определяне на индекса на Милър

При изчисляване индекса на Милър за една кристална решетка се извършват следните стъпки:

• Намират се точките на пресичане на плоскостта на кристалната решетка с осите X, Y и Z от координатната система.
• Взимат се реципрочните стойности на координатите на тези точки.
• Преработват се до начин, удобен за ползване, като вместо тях за стойности на индекса се приемат най-малките цели числа, отговарящи на математическите отношения между тези реципрочни стойности.^[8]

Съществуват няколко варианта на пресичане на осите на координатната система от плоскостите на кристалната решетка.^[6]

• Пресичане само на една от осите
• Пресичане на две от осите. Стени, които са успоредни на една от кристалографските оси се обозначават като призматични стени.
• Пресичане и на трите оси. Стените, които пресичат и трите кристалографски оси се наричат пирамидални стени.
• Пресичане на равни разстояния от началото на координатната система
• Пресичане на различни разстояния от началото на координатната система.^[5]

Индекс на Милър при кубична кристална решетка

Плоскости на кристалната решетка, успоредни на осите Y и Z^[6]

Най-простият вариант се получава, когато се разгледа кубична кристална решетка, на която една от плоскостите е успоредна на осите Y и Z. В такъв случай тя пресича оста X в точка A, а останалите две оси Y и Z – в безкрайността, тъй като плоскостта е успоредна на техните направления. Следователно пресичането на плоскостта на кристала с координатните оси става в точките A, ${\displaystyle \infty }$ и ${\displaystyle \infty }$. Винаги има кристална плоскост, успоредна на разглежданата, която пресича оста X в точка на разстояние 1 от началото на координатната система. Индексът на Милър се получава като се вземат реципрочните стойности на това пресичане, т.е.

Пресичане на плоскостта – ${\displaystyle {\frac {1}{1}$ : ${\displaystyle {\frac {1}{\infty }$ : ${\displaystyle {\frac {1}{\infty }$. Тъй като ${\displaystyle {\frac {1}{1}=1}$, а ${\displaystyle {\frac {1}{\infty }=0}$

за индекса на Милър се получава (1,0,0) и се записва като (100) в кръгли скоби.

Плоскости на кристалната решетка, успоредни на осите X и Y.^[6]

Когато плоскостта на кристалната решетка е успоредна на направленията на осите X и Y, то тя пресича оста Z в точка на разстояние 1 от началото на координатната система, а осите X и Y – в безкрайността. Следователно пресичането на плоскостта на кристала с координатните оси става в точките ${\displaystyle \infty }$, A и ${\displaystyle \infty }$. Аналогично на горния пример, отношението между реципрочните стойности на това пресичане са:

${\displaystyle {\frac {1}{\infty }$ : ${\displaystyle {\frac {1}{\infty }$ : ${\displaystyle {\frac {1}{1}$. И тъй като ${\displaystyle {\frac {1}{1}=1}$, а ${\displaystyle {\frac {1}{\infty }=0}$, а самото пресичане става в точките (0,0,1)

за индекса на Милър се получава (001).

Плоскости на кристалната решетка, успоредни на осите X и Z.^[6]

Ако плоскостта на кристалната решетка е успоредна на направленията на осите X и Z, тя ги пресича в безкрайността, а оста Y – в точка на разстояние 1 от началото на координатната система. Тогава, аналогично на горните два примера, индексът на Милър се получава (010)

Плоскости на кристалната решетка, успоредни само на една от осите.^[6]

Когато плоскостта на кристалната решетка е успоредна на оста Z и пресича осите Х и Y на равни разстояния, винаги ще има плоскост, при която тези равни разстояния са единица. В този случай пресичането на осите става в точки с координати по Х – (1,0,0), по Y – (0,1,0) и по Z – в ${\displaystyle \infty }$, то техните реципрочни стойности стават

${\displaystyle X=1\,}$, ${\displaystyle Y=1\,}$, ${\displaystyle Z=0\,}$. Тяхното отношение става ${\displaystyle 1\,}$ : ${\displaystyle 1\,}$ : ${\displaystyle 0\,}$

В такъв случай индексът на Милър се изразява с цифрите (110), затворени в кръгли скоби.

Аналогично, ако плоскостта на кристалната решетка пресича на равни разстояния осите Х и Z и е успоредна на оста Y, за индекс на Милър се получава (101). А ако пресича на равни разстояния осите Y и Z и е успоредна на оста Х, индексът на Милър се изразява с цифрите (011)

Плоскости, пресичащи на равни разстояния и трите оси.^[6]

Възможно е плоскостта на кристалната решетка, или успоредна на нея, да пресича едновременно и трите координатни оси и то на равни разстояния от началото на координатната система. Тогава точката на пресичане по оста Х има координати (1,0,0), по Y – (0,1,0) и по Z – (0,0,1). В този случай, базирайки се на казаното дотук, индексът на Милър се получава (111).

Повърхностите с индекси (001), (010), (100), (011), (101), (011) и (111) се наричат повърхности с нисък индекс при кубичната кристална система. Такива са всички кристални плоскости, при които индексът на Милър съдържа само единици и нули.

Плоскости, пресичащи на различни разстояния и трите оси.^[4]

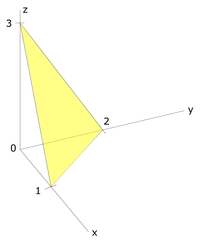
В най-общия случай плоскостта на кристалната решетка пресича и трите оси на координатната система на различни разстояния. В случая координатите на пресечните точки са: по оста Х – (1,0,0), по оста Y – (0,2,0) и по оста Z – (0,0,3) Тъй като индексът на Милър се получава от реципрочните стойности на координатите на тези точки, то за конкретния случай, илюстриран на схемата вляво, бихме получили

${\displaystyle {\frac {1}{1}$ : ${\displaystyle {\frac {1}{2}$ : ${\displaystyle {\frac {1}{3}$ След привеждане под общ знаменател се получава ${\displaystyle {\frac {6}{6}$ : ${\displaystyle {\frac {3}{6}$ : ${\displaystyle {\frac {2}{6}$

Най-малките цели числа, които имат същото отношение помежду си са 6:3:2, определят и индекса на Милър за съответната кристална плоскост на (632).

Когато индексите на дадена кристална форма са представени с числа по-големи от 9, те се отделят с точки, например (8.12.2).^[5]

Плоскости, пресичащи осите на разстояния, по-малки от 1.^[6]

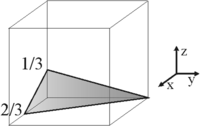
Има случаи, когато кристалната плоскост пресича координатните оси на разстояние по-малко от единица. Например при плоскост, която пресича оста Х на разстояние 2/3 от началото на координатната система, пресича Y на разстояние 1, а оста Z на разстояние 1/3. В този случай реципрочните стойности са:

${\displaystyle {\frac {3}{2}$ : ${\displaystyle {\frac {1}{1}$ : ${\displaystyle {\frac {3}{1}$ След привеждане под общ знаменател се получава ${\displaystyle {\frac {3}{2}$ : ${\displaystyle {\frac {2}{2}$ : ${\displaystyle {\frac {6}{2}$

Най-малките цели числа, които имат същото отношение помежду си са 3:2:6 и определят индекса на Милър за съответната кристална плоскост на (326).^[6]

Поради симетрията на кубичните кристали индексът на Милър за някои плоскости съдържа кратни едно на друго числа. В тези случаи той може да бъде опростен чрез обикновено съкращаване на числата. Например индексите (200) и (100) са идентични, тъй като се отнасят за успоредни една на друга плоскости.^[4]

Плоскости, пресичащи осите в областта на отрицателни стойности на координатната система.^[4]

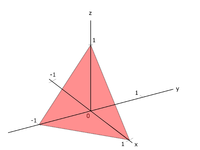
Когато кристалните плоскости пресичат една или няколко оси от координатната система в отрицателната им част, съответните цифри от индекса на Милър също получават отрицателни стойности. В илюстрирания на схемата вляво случай отрицателна стойност (-1) имаме по оста Y, а по осите Х и Z стойностите са (+1). В този случай в индекса на Милър трябва да се запишат числата (1,-1,1) и той придобива следния вид: (111), като минусът се записва вместо пред, над съответната цифра.

В примера на дясната схема кристалната плоскост пресича оста X в отрицателната ѝ част. При нея за индекс на Милър се получава (111).

Индекс на Милър при хексагонални и ромбоедрични структури^[9]

За удобство при кристали с хексагонална и тригонална сингония към триосната координационна система се добавя четвърта координатна ос, маркирана обикновено с u, която сключва равни ъгли от 120° (2π/3) с осите x и y и е перпендикулярна на хексагоналната ос z. Осите x, y и u лежат върху повърхнината на шестоъгълната основа, а оста z е перпендикулярна на всяка една от тях. По координатната ос x за индекса на Милър се отчита стойността h, по y – стойността k, по u – стойността i и по z – стойността l. В тази четириосна система (x,y,z,u) всяка стена от елементарната кристална клетка пресича координатните оси, отсичайки от тях различни части. На базата на тази система в индекса на Милър се въвеждат вместо три, четири цифри и той придобива следния вид – (h k i l) като сборът от първите две цифри трябва да е равен на отрицателната стойност на третата цифра:

${\displaystyle h+k+i=0\,}$ или ${\displaystyle h+k=-i\,}$

При този случай h, k и l са обикновените индекси на Милър, а i е като допълнителен индекс.^[5]

Равнината на дадената схема пресича оста x в точка P на разстояние ${\displaystyle 1\,}$, оста y – в точка Q също на разстояние ${\displaystyle 1\,}$, оста u в точка S на разстояние —-${\displaystyle {\frac {1}{2}$ и оста z в точка R на разстояние ${\displaystyle {\frac {1}{2}$. Стойностите на тези координати са:

${\displaystyle {\frac {1}{1}$ : ${\displaystyle {\frac {1}{1}$ : —-${\displaystyle {\frac {1}{2}$ : ${\displaystyle {\frac {1}{2}$, а техните реципрочни стойности се получават ${\displaystyle 1\,}$ : ${\displaystyle 1\,}$ : —-${\displaystyle 2\,}$ : ${\displaystyle 1\,}$. Следователно индексът на Милър за дадената на схемата плоскост е (1122).

Източници