2-3 strom
2-3 strom je druh stromu, jehož každý vnitřní uzel má buď dva potomky a obsahuje jeden klíč, nebo má tři potomky a obsahuje dva klíče. Všechny listy leží ve stejné hloubce.
2-3 stromy lze považovat za B-stromy obsahující vnitřní uzly pouze s dvěma nebo třemi potomky, respektive za B+ stromy, pokud přidáme podmínku, že všechna data leží v listech.
Díky stejné hloubce listů se 2-3 strom řadí mezi vyvážené stromy. Hloubka 2-3 stromu s n prvky se pohybuje v rozmezí mezi log3n a log2n, podle použité struktury. Tomu odpovídá i náročnost operací jako je vyhledávání, vkládání a odebírání dat z 2-3 stromu. 2-3 stromy jsou izometrické k AA stromům, tzn. jsou to ekvivalentní datové struktury. Jinými slovy, pro každý 2-3 strom existuje alespoň jeden AA strom s prvky ve stejném pořadí.


Historie
Vyvážené stromy se objevují v různých podobách, využívají se v datových strukturách pracujících na bázi seznamů nebo databází, kde se pracuje s operacemi vyhledávání, přidávání a mazání záznamů. Jako první představil 2-3 strom v roce 1970 John Hopcroft, bylo to vylepšení vyváženého binárního stromu. Později Rudolf Bayer a Ed McCreight zobecnili 2-3 strom pod pojmem B-strom, který byl dále zjednodušen do formy červeno-černého stromu.
Pravidla 2-3 stromu
- Všechny cesty od kořene k listům jsou stejně dlouhé.
- Data jsou zapsána v listech v poslední úrovni stromu.
- Listy jsou seřazeny podle klíče zleva (minimum) doprava (maximum).
- Jestliže vnitřní část uzlu obsahuje jeden klíč, uzel má dva potomky. Pokud vnitřní část uzlu má dva klíče, má uzel tři potomky.
Možné podoby stromu
- Strom je prázdný.
- Uzel nemá žádné potomky, v tom případě je listem.
- Vnitřní část uzlu obsahuje jedno pole s klíčovým atributem. Uzel má dva potomky.
- Vnitřní část uzlu obsahuje dva klíčové atributy. Uzel má tři potomky.
Organizace dat v 2-3 stromu

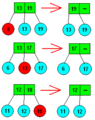
Vnitřní uzly neobsahují uvnitř data, ale obsahují některé informace o tom co je uloženo v jejich potomcích (podstromech). Tak jak je to zobrazeno na obrázku 1, kde levá vnitřní část pole (min S2) obsahuje minimální klíč ležící v prostředním podstromu (S2) a pravá vnitřní část uzlu (min S3) obsahuje minimální klíč ležící v pravém podstromu (S3). Stejně jako je tomu s uzlem se dvěma potomky. To z 2-3 stromů dělá tzv. vyhledávací stromy.
Při vkládání a mazání dat z 2-3 stromu je zapotřebí upravovat strukturu stromu, přizpůsobovat klíče v uzlech podle složení klíčů v listech a popřípadě měnit hloubku tohoto vyváženého stromu. U 2-3 stromu není zapotřebí tak často vyvažovat strom jako u binárního stromu, protože všechny listy jsou na stejné úrovni. Avšak je zapotřebí daleko častěji vyvažovat 2-3 strom než b-strom nebo 2-3-4 strom, kde je možné mít daleko více potomků u jednoho uzlu.
Příklad
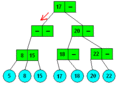
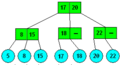
Dva příklady 2-3 stromů s uloženými prvky 2, 5, 6, 8, 15, 17, 18 a 22.
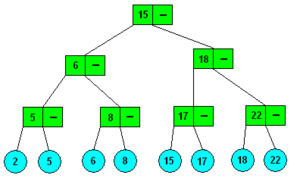

2-3 stromy se stejnými daty mohou mít odlišnou strukturu. Pokud 2-3 strom obsahuje převážně uzly se dvěma potomky (větší hloubka stromu) vzrůstá náročnost operací (např. vyhledávání) s 2-3 stromem o n prvcích z O(log3n) na O(log2n).
Operace s 2-3 stromem
2-3 stromy se využívají v datových strukturách jako jsou seznamy nebo databáze, kde se pracuje se základními operacemi vyhledávání, vkládání a mazání prvků. Usnadňují tak daleko více práci s daty, než kdybychom měli data uspořádána libovolně v paměti (obtížné vyhledávání) nebo naopak uložená jako seznam v řadě za sebou (obtížné vkládání).
Operace vyhledávání
Při vyhledávání dat podle klíče začínáme u Kořene stromu a postupujeme podle klíčových atributů shora dolů.
- Procházíme uzel se dvěma potomky viz obrázek 4.
- Pokud hledaný klíč K je menší než klíčový atribut uzlu K1, hledáme dále v levém podstromu.
- Jestliže hledaný klíč K je větší nebo roven K1, pak hledáme dál v pravém podstromu.

- Procházíme uzel se třemi potomky viz obrázek 5.
- Pokud hledaný klíč K je menší než klíčový atribut uzlu K1, hledáme dále v levém podstromu.
- Jestliže je hledaný klíč K větší nebo roven K1 a zároveň pokud je ve vnitřní části uzlu klíčový atribut K2 větší než K pak hledáme v prostředním podstromu.
- Pokud K je větší nebo rovno K2, hledáme dále v pravém podstromu.

Tímto způsobem pokračujeme, až do poslední úrovně stromu, kde se nachází listy s daty.
Operace vkládání

Při vkládání nové větve do 2-3 stromu je nutné vyhledat pozici, kam novou větev vložíme. Poté, co je nalezena pozice, vložíme větev do příslušného rodiče r.
- Jestliže počet potomků rodiče r se rozšíří ze dvou na tři u 2-3 stromu můžeme daný prvek rovnou vložit.
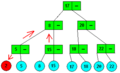
- Pokud počet potomků r po vložení se zvýší ze tří na čtyři, r se rozdělí na dva uzly po dvou potomcích a tím se zvýší počet potomků předka r o jeden viz obrázek 6.
Pokud se zvýší počet potomků r postupujeme obdobným způsobem směrem nahoru dokud nenarazíme na předka se dvěma potomky nebo na kořen se třemi potomky, kdy se zvýší hloubka 2-3 stromu o jedna, jak je zobrazeno postupně na obrázcích 7, 8, 9, 10.
-
Obrázek 7: Vyhledání místa ve 2-3 stromu, kam se vloží list.
-
Obrázek 8: Vložení listu do uzlu a následná příprava dělení uzlu na dva. Převedení čísla 20 do rodičovského uzlu.
Při každém vkládání je nutné přizpůsobit dané klíče uzlů podmínkám 2-3 stromu. Pro vkládání je možné využívat i složitější algoritmy, kde se nejdříve přizpůsobí struktura stromu vkládání. Například se přesune prvek (podstrom) do sousední větve, která není tolik zaplněná a tím se usnadní následné vkládání.
Operace mazání
Nejprve je nutné vyhledat větev, kterou budeme odebírat. Poté se odebere větev z jejího rodiče r.
- Pokud se sníží počet potomků r ze tří na dva u 2-3 stromu provedou se jednoduché změny viz obrázek 11.
- Jestliže počet potomků r se sníží ze dvou na jeden
- r se sloučí se svými dvěma sourozenci a vzniknou tak dvě větve, které si rozdělí potomky.
- r převezme jednu větev z jednoho ze svých sourozenců, který leží vedle.
- Pokud po odebrání r má dohromady se svým sourozencem jen tři potomky vezme si r jednu větev ze svého rodiče.
Obdobným způsobem se pokračuje směrem nahoru a v případě potřeby se sníží hloubka 2-3 stromu o jedna, jak je to zobrazeno na obrázcích 12, 13, 14, 15, 16.
-
Obrázek 11: Odebrání prvku z uzlu se třemi potomky.
-
Obrázek 12: Příklad odebrání listu s číslem 6.
-
Obrázek 13: Odebrání prvku s číslem 2, sloučení uzlů. Další operace znázorněné na obrázcích 9, 10, 11.
-
Obrázek 14: Sloučení dvou uzlů do jednoho a vyprázdnění jejich předka. Následuje přesun uzlu s číslem 17 do prázdného uzlu.
-
Obrázek 15: Převedení čísla 17 do prázdného uzlu, příprava na sloučení s uzlem s číslem 20.
-
Obrázek 16: Výsledek: sloučení uzlů do jednoho kořene a snížení hloubky stromu o jedna.
Operace jakou je vkládání a mazání se dají řešit různými algoritmy. Můžeme například nejdříve změnit strukturu stromu tak, abychom mohli jednoduše vložit nebo vyjmout větev. Můžeme provádět různá přeskupení, abychom využili, co nejvíce uzly se třemi potomky, kde je méně náročné vyhledávání, mazání dat a také jsou zde menší nároky na paměť počítače.
Poznámky
Vytvořený 2-3 strom se může lišit od zde uvedených příkladů. Například listy mohou být uzly se dvěma klíči (daty) a data se nemusí vyskytovat jen v listech, ale v každém uzlu. Tímto způsobem se dají snížit nároky na paměť a některé operace se stromem.
Související články
- B-strom
- (a,b)-strom
- 2-3-4 strom
Externí odkazy
 Obrázky, zvuky či videa k tématu 2-3 strom na Wikimedia Commons
Obrázky, zvuky či videa k tématu 2-3 strom na Wikimedia Commons
- Vizualizace 2-3 stromu
- (anglicky)2-3 strom Archivováno 17. 9. 2020 na Wayback Machine.
- (anglicky)Vyvážené stromy: 2-3 strom