Cosinus
 Der er for få eller ingen kildehenvisninger i denne artikel, hvilket er et problem. Du kan hjælpe ved at angive troværdige kilder til de påstande, som fremføres i artiklen.
Der er for få eller ingen kildehenvisninger i denne artikel, hvilket er et problem. Du kan hjælpe ved at angive troværdige kilder til de påstande, som fremføres i artiklen.
Cosinus er en trigonometrisk funktion inden for matematikken, som beskriver bestemte forhold mellem siderne i en retvinklet trekant, eller x-koordinaten til et punkt på enhedscirklen. I matematiske formler forkortes cosinus til cos, og tager man cosinus til en vinkel θ, skrives det matematisk som: cos θ. Cosinus-funktionen har mange træk tilfælles med en anden trigonometrisk funktion, sinus, som beskriver y-koordinaten til føromtalte punkt på enhedscirklen, og disse to funktioner danner grundlag for en tredje trigonometrisk funktion; tangens.
Grafen for cosinus (og sinus) udviser et karakteristisk bølgemønster, som kan bruges som model af en lang række matematiske og fysiske fænomener.
Cosinus i trekant
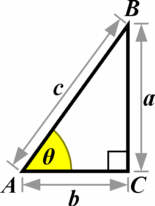
For en trekant gælder, at cosinus til en af de to vinkler der ikke er rette er lig med forholdet mellem trekantens hypotenuse og den hosliggende katete. For trekanten på illustrationen til højre gælder, at cosinus til den vinkel θ der er markeret med gul farve, er lig med forholdet mellem længderne af siderne b og c, dvs.:
Selv om denne definition bygger på en retvinklet trekant, bruges cosinus-funktionen i beregninger over alle mulige trekanter i planen, med eller uden rette vinkler – bl.a. i de såkaldte cosinusrelationer.
Cosinus i enhedscirklen

Definitionen med den retvinklede trekant kan redegøre for cosinus til vinkler mellem 0 og 90 grader, men ved hjælp af enhedscirklen kan man udvide definitionsmængden til cosinus til alle reelle tal.
På Illustrationen til højre ses enhedscirklen, hvori er indtegnet nogle centervinkler hvis ene ben falder sammen med x-aksen (i pilens retning). Det andet ben skærer cirklens periferi i et punkt, hvis x-koordinat (markeret med små kvadrater), eller afstand til y-aksen, er lig med cosinus til den pågældende centervinkel.[1]
Centervinkler måles med den positive side af x-aksen som »nulpunkt«. Går man »mod uret« når man måler vinklen, regnes denne vinkel positivt, mens vinklen er negativ hvis man »måler medurs«.
Egenskaber

Kurven til højre viser hvordan cosinus til en vinkel θ varierer for vinkler mellem ±360° (nederste vandrette skala). Som nævnt er cosinus defineret for ethvert reelt tal θ – ud over det viste interval fortsætter kurven i det samme bølge-mønster uendeligt langt til begge sider.
Man kan se at kurven aldrig kommer ud over intervallet fra -1 til 1 på y-aksen: Den såkaldte værdimængde til cosinus er netop alle reelle tal fra og med -1 til og med 1.
Cosinusfunktionen (for vinkler givet i buemål, mere herom senere) er kontinuert og differentiabel: Stamfunktionen, eller det ubestemte integral, til cos v er sin v, og den afledede funktion af cos v er -sin v.
Vinkelmål
Det tal man i praktiske beregninger tager cosinus af, repræsenterer så godt som altid en vinkel, eventuelt en såkaldt fasevinkel – af den grund skal man, når man beregner cosinus, være sikker på hvilken måleenhed vinklen er opgivet i. I teoretisk arbejde, f.eks. matematiske og fysiske beregninger, bruges den lidt specielle enhed radian; vinklens buemål eller »naturlige vinkelmål«, med mindre andet udtrykkeligt er angivet. I toppen af grafen ovenfor er indsat en skala der angiver vinklen udtrykt i radianer.
I andre, mere praktisk orienterede sammenhænge, findes en række forskellige måleenheder – kategorien vinkelenheder giver en oversigt over artikler om relevante måleenheder.
Matematiske lommeregnere har almindeligvis en tast og nogle små bogstaver i displayet til at vælge mellem »D« for »almindelige« grader, »G« for såkaldte nygrader og »R« for førnævnte radianer: Man skal have valgt det rigtige mål inden man trykker på en trigonometrisk funktion.
Cosinus til visse vinkler
For nogle få, »specielle« vinkler kan man ad geometrisk vej finde frem til eksakte værdier for cosinus til disse vinkler. Tabellen til højre giver et overblik.
| Vinkel a | cos a | |||
|---|---|---|---|---|
| Grader | Radianer | Nygrader | Eksakt | Decimalbrøk |
| 0° | 0 | 0g | 1 | 1 |
| 15° | 16 2/3g | 0,965925826289068 | ||
| 30° | 33 1/3g | 0,866025403784439 | ||
| 45° | 50g | 0,707106781186548 | ||
| 60° | 66 2/3g | 0,5 | ||
| 75° | 83 1/3g | 0,258819045102521 | ||
| 90° | 100g | 0 | 0 | |
| 105° | 116 2/3g | -0,258819045102521 | ||
| 120° | 133 1/3g | -0,5 | ||
| 135° | 150g | -0,707106781186548 | ||
| 150° | 166 2/3g | -0,866025403784439 | ||
| 165° | 183 1/3g | -0,965925826289068 | ||
| 180° | π | 200g | -1 | |
Ved at studere illustrationen med enhedscirklen kan man slutte sig til, at x-koordinaten til skæringspunktet med cirkelperiferien bliver den samme uanset om man måler vinklen »med«- eller »modurs«. Matematisk gælder, at:
cos x = cos -x
For tabellen til højre betyder dette, at hvis cosinus til f.eks. 60° er 0,5, så er cosinus til -60° også lig med 0,5.
Endvidere gælder, at eftersom cosinus er periodisk, er cos x = cos (x + n·360°) hhv. cos x = cos (x + n·2·π) hhv. cos x = cos (x + n·400g), hvor n er et helt tal.
Invers cosinus
Hvis man »indskrænker« definitionsmængden for cosinus til intervallet fra 0° til 180° (0 til 200 nygrader eller 0 til π radianer), får man en såkaldt monoton eller »én-til-én-tydig« funktion, og til sådanne funktioner kan opstilles en såkaldt invers funktion, som populært sagt »regner baglæns« fra cosinus til en vinkel og tilbage til vinklen. For cosinus' vedkommende kaldes denne inverse funktion for invers cosinus.
Referencer
- ^ Holth (1987) s. 56-61
Eksterne henvisninger
Online-værktøjer, der udregner siderne og vinklerne på en trekant for dig:
- CosSinCalc
- http://carbidedepot.com/formulas-trigright.asp
- http://www.mathwarehouse.com/triangle-calculator/online.php
Bog
- Holth, Klaus m.fl. (1987): Matematik Grundbog 1. Forlaget Trip, Vejle. ISBN 87-88049-18-3






















