Tronco (geometría)
| tronco | |
|---|---|
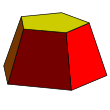  Ejemplos: Un tronco pentagonal y otro cuadrado | |
| Caras | n trapezoides, 2 polígonos |
| Aristas | 3n |
| Vértices | 2n |
En geometría, un tronco es la porción resultante de un sólido, normalmente un cono o pirámide, cortado con dos planos paralelos. Las intersecciones del sólido con un plano cortante son las bases. El eje es el mismo que el del objeto original, si este lo tuviera. Si el eje es perpendicular a la base el sólido es recto, y en caso contrario, oblicuo.
Elementos y casos especiales
Cada una de las intersecciones con los planos de corte es una base del tronco. El eje, si lo hubiere, es el original del cono o la pirámide. Un tronco es circular si tienen esa forma las bases; es recto si el eje es perpendicular a las bases y oblicuo en caso contrario.
Conos y pirámides pueden verse como casos extremos de tronco, en los que uno de los planos de corte es tangente al vértice, quedando esta reducida a un punto.
Fórmulas

Para calcular el área total y el volumen de esta figura geométrica necesitamos saber el perímetro y el área de los planos cercano (p y B respectivamente) y lejano (p' y B' respectivamente), su altura (h), que corresponde a la recta que une perpendicularmente los dos planos, y su apotema (a).
Área total:
Volumen:
El volumen de un tronco es la diferencia entre el volumen del sólido original y el de la parte exterior a los planos de corte:
donde y son las distancias desde el vértice a las bases mayor y menor, siendo y las áreas de estas.

Sea la altura del tronco, esto es la distancia entre las bases, y teniendo en cuenta que y que , se obtiene una fórmula para el volumen, donde se relaciona este con la altura del tronco y el área de sus bases, mediante la media heroniana.
Tronco cónico
En particular, el volumen de un tronco cónico es:
donde y son los radios de las bases.
Tronco circular
Usando las definiciones precedentes, en el caso de un cono truncado, la fórmula se simplifica:
- , siendo 'D' los diámetros de las bases.
De igual forma:
Aplicaciones en la fotografía
El tronco se utiliza en el campo de programas de edición fotográfica digital o los gráficos 3D.
En el campo de la fotografía el tronco se usa como representación del volumen de visualización de una cámara (ya sea de vídeo o de fotografía fija). En este caso se usa un tronco piramidal con seis planos, los cuales son:
- Plano de recorte lejano (far).
- Plano de recorte cercano (near).
- Plano superior (top).
- Plano inferior (bottom).
- Plano izquierdo (left).
- Plano derecho (right).
En el vértice de la pirámide original se sitúa el observador, el plano de recorte cercano define la mínima distancia de enfoque y el plano de recorte lejano es la máxima distancia de enfoque.
En el ámbito del diseño 3D se utilizan los cálculos matemáticos descritos anteriormente para el tronco de seis lados para simular el comportamiento de una cámara virtual. Así se consiguen resultados de planos semejantes a la realidad. En concreto, los softwares de renderizado usan esta figura geométrica para calcular la parte del escenario virtual que ve la cámara o el observador imaginario.
Véase también
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Tronco.
Wikimedia Commons alberga una categoría multimedia sobre Tronco.- Weisstein, Eric W. «Tronco piramidal». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Tronco cónico». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Derivation of formula for the volume of frustums of pyramid and cone (Mathalino.com)
- Modelos de papel de troncos de pirámides
- Weisstein, Eric W. «PyramidalFrustum». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- http://geeks.ms/blogs/jbosch/archive/2009/10/24/xna-frustum-culling-en-xna.aspx
- https://web.archive.org/web/20100217033932/http://knol.google.com/k/view-frustum















