Bohrren eredu atomikoa

Bohr-en eredu atomikoa[1] Niels Bohr-ek[2] proposatutako eredu atomikoa da, Rutherforden urre xafla saiakuntzan lortutako emaitzetan oinarrituta dago. Bohr-en eredua, Rutherfordenaren antzera, planetarioa da, hau da, erdian positiboki kargaturiko nukleo bat dauka eta elektroiak, beraien karga negatiboarekin, nukleo honi biraka dabiltza. Grabitazio indarraren ordez, energia elektrostatikoak tokian mantentzen ditu. Plancken energiaren izaera kuantikoan oinarrituta, Bohrrek elektroien orbitak diskretuak direla proposatu zuen, hau da, elektroien orbitak energia zehatz batzuk bakarrik izan ditzakete. Thomsonen eredu atomikoaren jarraitzailea izan zen eta Rutherfordek lehenago proposatutako eredu atomikoaren hobekuntza bat zenez, askotan Rutherford-Bohr eredu atomiko bezala ere ezagutzen da.
1913an proposatu zuen Bohr-ek bere eredua eta arrakasta Rydberg formulak hidrogenorako aurresaten zituen espektroen lerroak azaltzearekin batera etorri zen. Bohrren ereduaren aurretik Rydberg formula esperimentalki frogatuta zegoen baina teorikiko ezin zen azaldu. Bohrren azalpenak Rydbergen formularen emaitzei oinarri teorikoa emateaz gain, formulan funtsezko konstante fisiko hainbat zeudela ere frogatu zuen.
Bohrren eredua hidrogenozko atomoaren eredu sinple bat da baina hainbat sistemetarako balio du. Horregatik gaur egun mekanika kuantikoaren sarrera bezala erakusten da ikastokietan, nahiz eta berez Bohrren eredua teoria zientifiko zaharkitua izan.
Historia
XX. mendearen hasieran Ernest Rutherford eta beste hainbat fisikariek egindako hainbat saiakuntzetan atomoak erdialdean positiboki kargatutako nukleo txiki eta dentso bat zeukala egiaztatu zuten, negatiboki kargatutako elektroi laino lauso bat ingurunean dagoela. Informazio esperimental honekin Rutherfordek atomoaren eredu planetarioa aurkeztu zuen, 1911ko Rutherforden eredua izenarekin ezagutzen dena.
Eredu honen arabera atomoaren nukleoa zentroan dago eta elektroiak horren inguruan orbitak deskribatzen dituzte, baina eredu honek akatz handi bat erakusten zuen: Mekanika klasikoaren arabera (Larmoren formula) elektroiak azeleratzean nukleoek erreadiazio elektromagnetikoa igorriko lukete; honen ondorioz, nukleo atomiko bat orbitatzean, azelerazio zentripetuagatik, elektroiak energia galtzen joango lirateke espiralean nukleora jauziz. Hau ezinezkoa da, atomoak estruktura egonkorrak baitira. Beste aldetik, XIX. mendearen bukaeran hidrogenoaren atomoaren espektroaren hutsuneak demostratzen zuten bakarrik uhin luzera diskretu zehatzetan erradiazioa igortzen zela, Balmer, hain zuzen, izan zen hidrogenoaren atomoan hutsune hauen arteko erlazio matematikoa aurkitu zuen lehenengoa
Honako arazo teorikoak konpontzeko Bohr-ek 1913 honako lau postulatuetan oinarritu zuen bere modelo atomikoa proposatzeko:
- Elektroiek ez dute erradiazio elektromagnetikorik igortzen orbitatzean, nukleoa orbitatzen dute distantzia zehatzeko orbitetan, elektroiak orbita horien zehar soilik mugi daitezke.
- Elektroia eta nukleoaren arteko elkarrakzioa elektrostatikoa da (Coulomb-en indarra). Elektroien orbitak nukleoarekiko zirkularrak dira.
- Elektroi orbita bakoitzak momentu angeluar bakarra dauka finkatuta, momentu angeluar hori kuantizatuta dago, hau da, balio diskretuak hartzen ditu soilik. Balio horiek Plancken konstantearekiko proportzionaltasuna mantentzen dute non zenbaki osoa den eta Planck-en konstante laburtua.
- Planken ereduaren arabera elektroiek energia gal edo irabaz dezakete bakarrik orbita batetik bestera pasatzeko. Energia minimo hori gainditzen ez bada elektroiak ez du energia xurgatuko; era berean, elektroiak fotoi bat askatzen badu fotoiak lehen hurbilketan bi orbiten arteko energia diferentzia izango du.
Elektroien energia mailak
Bohrren ereduak zehaztasun handiko emaitzak ematen ditu atomo hidrogenoideetan, hau da, nukleo bat eta elektroi bakar bat duten atomoak. Atomo hidrogenoide batzuk dira: hidrogenoa (H), helio ionizatua (He+), bi aldiz ionizaturiko litioa (Li++), positroia (Ps) eta Rydberg-en formula[3] jarraitzen duten atomoak.
Indar elektroestatikoen eraginez, elektroiak orbita zirkularrak egingo ditu nukleoaren inguruan. Nukleoaren masa elektroiarena baino askoz ere handiagoa dela onartzen da. Guzti hau kontutan hartuz, mekanika klasikoaren arabera, sistema honetan indar zentripetua Coulomb-en indarraren berdina izango da, hau da:
non elektroiaren masa den, elektroiaren karga elektrikoa, zenbaki atomikoa eta elektroiaren nukleoarekiko distantzia (elektroiaren orbitaren erradioa). Ekuazio honetatik, elektroiaren abiadura lor dezakegu edozein erradioko orbitetarako:
Gainera, Bohr-en 3. postulatuaren arabera, orbitatzen ari den elektroiaren momentu angeluarra hurrengoa da:
non n zenbaki osoa den.
Momentu angeluarraren adierazpena eta abiadurarena berdinduz eta r askatuz, eredu honek baimenduriko erradioen hurrengo adierazpena dugu:
non Bohr-en erradioa den. Ikus daitekenez, erradioak kuantizatuta daude, eta Z = 1 kasurako oinarrizko orbitaren erradioa () da.
Abiadura ere kuantizatuta dago. Erradioaren adierazpena Bohr-en momentu angeluarraren adierazpenan sartuz eta abiadura bakanduz hurrengoa lor dezakegu:
Behin abiadura jakinda, elektroiaren energia totala ere jakin dezakegu edozien orbitetarako:
Beraz, oinarrizko energia () hau da,
Ohartu gaitezke energia kuantizatuta dagoela ere eta negatiboa izateaz gain erradioarekiko alderantzizko proportzionala dela. Hau hurrengo moduan interpreta daiteke: elektroia nukleotik urruntzeko energia behar da. Beraz, elektroia nukleotik izugarri urrun degoenean (distantzia infinitutzat hartzeko beste), energia hau zero izango da.
Rydberg-en formula
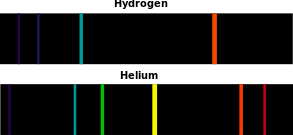
Rydberg-en formula[3], Bohr-en formula baino lehen enpirikoki ezaguna zena, energia maila orbital desberdinen arteko trantsizio energiak deskribatzen ditu Bohr-en teorian. Bohr-en formulak jadanik ezaguna zen Rydberg-en konstantearen balioa ematen du, baina naturako oinarriagoak diren konstanteen funtzioan, elektroiaren karga eta Planck-en konstantea batik bat.
Elektroi bat hasierako energia maila batetik maila handiago batera pasatu ondoren hasierako posiziora saltoka bueltatu egiten da tarteko energia mailetatik pasatzen eta salto bakoitzean fotoi bat emititzen du. Atomo hidrogenoideen energia mailetarako deribatutako formula erabiliz atomo hauek emititu ditzaketen argi izpien uhin-luzerak ondorioztatu daitezke.
Atomo hidrogenoide batek emititutako fotoi baten energia atomo honen bi energia mailen arteko energien aldeagatik emanda dago. Aurretik lortutako energiaren adierazpenetik:
non amaierako energia maila den, hasierako energia maila eta atomoaren energia maila txikiena den.
Planck-en formularen arabera fotoi baten energia hurrengoa da:
Aurreko bi formulak erabiliz, atomo hidrogenoideak emititutako fotoi baten uhin luzera hau da:
Formula hau Rydberg-en formula eta aplikagarria izateko izan behar da, bestela uhin luzera negatiboa dugu, zentzu fisikorik gabeko emaitza. Izan ere, kasuan elektroia orbitaz aldatzeko energia behar du eta ondorioz fotoi bat emititu beharrean xurgatu egingo du.
Formulan agertzen den balioari Rydberg-en konstantea deritzo. konstante fundamentalen mende idazten badugu Rydberg-en konstanterako hurrengo adierazpena lortzen dugu:
Formula hau jadanik XIX. mendean ezaguna zen espektroskopian aritutako zientizalarientzat, baina azalpen teorikorik ez zegoen Bohr-en teoriara arte. Horregatik, Bohr-en eredutik Rydberg-en konstantea ondorioztatu ahal izatea eta Bohr-en formulak esperimentalki behatutako Lyman ( =1), Balmer (=2), eta Paschen (=3) serieetako lerro espektralekin erakutsitako erabateko adostasunak, eta garaian ezezagunak ziren beste serie batzuen aurreikuspen arrakastatzuak garrantzi handikoak izan ziren ereduak izan zuen berehalako onarpenean.
Franck-Hertzen esperimentua
Franck-Hertzen esperimentua, 1914. urtean, James Franck eta Gustav Hertz-ek Bohren ereduak proposatutako energia mailen kuantizazioa demostratzeko egindako esperimentua da[4]. Esperimentu horretan elektroiak azeleratzen dira potentzial diferentzia batean zehar; azeleratutako elektroi askeek merkurio atomoetakoko elektroiak kitzikatzeko energia minimoa lortzean energia zinetikoa galtzen dute, ondorioz zirkuituko tentsioa txikitzen da. Tentsio honen galera bakarrik lortzen da balio konkretu batzuetan, honen bidez demostratu zen atomoen energia mailak Bohrek deskribatu zituen bezalakoak direla.


Bohr-en ereduaren akatsak
Bohren ereduak zailtasunak ditu espektro atomikoan gertatzen den beste fenomeno bat azaltzeko. Hasieran hidrogenoaren espektroaren espekro-lerroak azaltzeko eredu egokia zela zirudien, baina benetan espektro-lerro bakoitzaren ingurune txiki batean begiratzean beste espektro-lerro batzuk agertzen ziren, eta hutsune hauek ezin dira azaldu bohren eredua erabiliz. Beste hutsune berri hauek azaldu ahal izateko Wilson eta Sommerfeldek aldaketa batzuk egin izan behar zuten, aldaketa horiek Wilson eta Sommerfelden ereduan[1] batzen dira.
Erreferentziak
- ↑ a b (Gaztelaniaz) Martínez, Jorge Enríquez Figueroa. (2007). Física Moderna Edición Revisada. Pearson Educación ISBN 9789702607892..
- ↑ (Gaztelaniaz) Química i. EUNED ISBN 9789968316262..
- ↑ a b (Frantsesez) Rydberg, J.R.. (1889). Researches sur la constitution des spectres d'émission des éléments chimiques. Kongliga Svenska Vetenskaps-Akademiens Handlingar [Proceedings of the Royal Swedish Academy of Science], 1-177 or..
- ↑ (Alemanez) Franck, J. & Hertz, G. (1914): Über Zusammenstöße zwischen Elektronen und den Molekülen des Quecksilberdampfes und die Ionisierungsspannung desselben. Verh. Deutsche Phys. Ges. 16, 457-467
Bibliografia
- Bohr, Niels. On the Constitution of Atoms and Molecules, Part I. Philosophical Magazine, 1–24 or. doi:. Bibcode: 1913PMag...26....1B..
- Bohr, Niels. (1913). On the Constitution of Atoms and Molecules, Part II Systems Containing Only a Single Nucleus. Philosophical Magazine, 476–502 or. doi:. Bibcode: 1913PMag...26..476B..
- Bohr, Niels. (1913). On the Constitution of Atoms and Molecules, Part III Systems containing several nuclei. Philosophical Magazine, 857–875 or. doi:. Bibcode: 1913PMag...26..857B..
- Bohr, Niels. (1914). The spectra of helium and hydrogen. Nature, 231-232 or. doi:. Bibcode: 1913Natur..92..231B..
- Bohr, Niels. (1921). Atomic Structure. Nature, 104–107 or. doi:. Bibcode: 1921Natur.107..104B..
- Einstein, Albert. (1917). Zum Quantensatz von Sommerfeld und Epstein. Verhandlungen der Deutschen Physikalischen Gesellschaft. Reprinted in The Collected Papers of Albert Einstein, A. Engel translator, (1997) Princeton University Press, Princeton. 6 p. 434. (provides an elegant reformulation of the Bohr–Sommerfeld quantization conditions, as well as an important insight into the quantization of non-integrable (chaotic) dynamical systems.)
Gehiago sakontzeko
- R. Eisberg & R. Resnick, "Física Cuántica", Editorial Limusa 1978, ISBN 978-968-18-0419-0



























