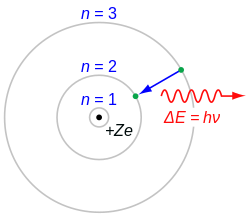
 模型所論電子,克乎殼層,繞核而動也。躍遷高軌,釋電磁波,至低軌,則取之。[一]電子軌道旌以灰圈,半徑自主量子數平方n2益增,遷三軌至二軌,為巴耳末系之第一譜線,色赤(波長六百五十六納米)。
模型所論電子,克乎殼層,繞核而動也。躍遷高軌,釋電磁波,至低軌,則取之。[一]電子軌道旌以灰圈,半徑自主量子數平方n2益增,遷三軌至二軌,為巴耳末系之第一譜線,色赤(波長六百五十六納米)。
玻爾模型,原子結構模型也。丹麥人玻爾倡之於一九一三年。量子化析之,究莫破電子之運動。初有芮得柏公式,論氫原子之譜線,今闡以模型也。
論
模型假定有二:
- 乎氫原子,電子繞核,為圓周運動。
- 軌動電子之角動量
 定量為正整數乘以約化普朗克常數
定量為正整數乘以約化普朗克常數  。
。
軌道半徑量子化
按假定一,電子繞核以圓,是謂經典軌。電子運動之向心力者,乃電磁力所得:
 ,
,
以  為電子質量,
為電子質量, 為電子速,
為電子速, 為電子軌道半徑,
為電子軌道半徑, 為電常數,
為電常數, 為基本電荷。
為基本電荷。
故得半徑
 ,
,
又可計圓周運動之角動量,為半徑動量之積:
 。
。
故,按假定二,有速
 ,
,
以  為主量子數,
為主量子數, 為約化普朗克常數。
為約化普朗克常數。
併以上兩式,可得
 。
。
又書
 ;
;
以  為玻爾半徑。
為玻爾半徑。
乎氫原子玻爾模型者,電子視核為圓心,又有量子化半徑,半徑之細極也。電子弗可更趨於核,電子以圓周加速運動,亦不放光矣。
軌道能量量子化
電子繞核之軌能  ,乃動能
,乃動能  、勢能
、勢能  之和:
之和:
 。
。
代軌道半徑式至上式,可得
 。
。
乎氫原子玻爾模型者,軌能有定量,反比於主量子數平方。此乃受縛電子之能也。若設核固定不動,則亦為氫原子之能量也。
躍遷能量變化
電子者定態,只存於能量穩態也。能量若有遷,則躍遷乎兩定態間,故電子只可為諸分立定態矣。若躍遷諸定態,則有食釋光波也:
 ,
,
以  為頻率。
為頻率。
代軌道能量式於上式,可得
 。
。
復書,得裡德伯公式:
 。
。
以  是裡德伯常數。
是裡德伯常數。
他山
攷

























