توزیع ارلانگ

ارلانگ

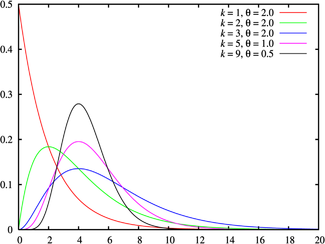
تابع چگالی احتمال
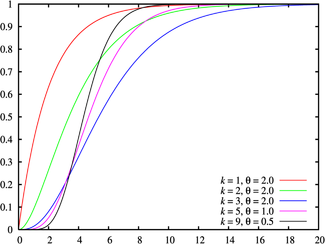
تابع توزیع تجمعی
پارامترها	${\displaystyle k>0\,}$ شکل (صحیح) نرخ رشد (حقیقی) ${\displaystyle \lambda >0\,}$ و یا: مقیاس (حقیقی) ${\displaystyle \theta =1/\lambda >0\,}$
تکیه‌گاه	${\displaystyle x\in [0;\infty )\!}$
تابع چگالی احتمال	${\displaystyle {\frac {\lambda ^{k}x^{k-1}e^{-\lambda x}{(k-1)!\,}$
تابع توزیع تجمعی	${\displaystyle {\frac {\gamma (k,\lambda x)}{(k-1)!}=1-\sum _{n=0}^{k-1}e^{-\lambda x}(\lambda x)^{n}/n!}$
میانگین	${\displaystyle k/\lambda \,}$
میانه	رابطه ساده صریح برای این پارامتر وجود ندارد
مُد	${\displaystyle (k-1)/\lambda \,}$ for ${\displaystyle k\geq 1\,}$
واریانس	${\displaystyle k/\lambda ^{2}\,}$
چولگی	${\displaystyle {\frac {2}{\sqrt {k}$
کشیدگی	${\displaystyle {\frac {6}{k}$
آنتروپی	${\displaystyle k/\lambda +(k-1)\ln(\lambda )+\ln((k-1)!)\,}$ ${\displaystyle +(1-k)\psi (k)\,}$
تابع مولد گشتاور	${\displaystyle (1-t/\lambda )^{-k}\,}$ for ${\displaystyle t<\lambda \,}$
تابع مشخصه	${\displaystyle (1-it/\lambda )^{-k}\,}$

توزیع ارلانگ توزیع احتمالی پیوسته‌ای است که به دلیل ارتباط آن با توزیع‌های نمایی و گاما دارای کاربردهای فراوانی است. این توزیع اولین بار توسط اگنر کراروپ ارلانگ، دانشمند دانمارکی، که بر روی تعداد تلفن‌های همزمان به یک اپراتور در ایستگاه سوئیچ مطالعه می‌کرد پیشنهاد شد.^[۱]