مکانیک کوانتومی

مکانیک کوانتوم
${\displaystyle i\hbar {\frac {\partial }{\partial t}|\psi (t)\rangle ={\hat {H}|\psi (t)\rangle }$ معادله شرودینگر
آشنایی واژه‌نامه · تاریخچه
پیش‌زمینه نشان‌گذاری برا-کت مکانیک کلاسیک هامیلتونی (مکانیک کوانتومی) تداخل امواج نظریه کوانتومی قدیمی
مفاهیم بنیادی همدوسی ناهمدوسی اصل مکملیت تراز انرژی درهم‌تنیدگی کوانتومی هامیلتونین اصل عدم قطعیت حالت پایه تداخل امواج اندازه‌گیری در مکانیک کوانتومی عدم موضعیت مشاهده‌پذیری عملگر (فیزیک) کوانتوم نوسان کوانتومی کف کوانتومی اثر کاسیمیر عدد کوانتومی نویز کوانتومی مکانیک کوانتومی حالت کوانتومی سیستم کوانتومی دورنوردی کوانتومی کیوبیت اسپین برهم‌نهی کوانتومی Symmetry (Spontaneous) symmetry breaking حالت خلاء انتشار موج تابع موج فروریزش تابع موج دوگانگی موج و ذره موج مادی
آزمایش‌ها افشار نامعادله بل دیویسون گرمر انتخاب تاخیردار دوشکاف فرانک هرتز ماخ-زندر بمب خنثی‌کن الیتزور فایدمن آزمایش پوپر پاک‌کن کوانتومی گربه شرودینگر اشترن-گرلاخ آزمایش انتخاب تاخیردار ویلر
فرمول‌بندی فرمول‌بندی ریاضی مکانیک کوانتم تصویر هایزنبرگ تصویر دیراک مکانیک ماتریسی تصویر شرودینگر فرمول‌بندی انتگرال مسیر فرمول‌بندی فضای فاز
معادلات معادله دیراک معادله کلاین-گوردون معادله پائولی فرمول ریدبرگ معادله شرودینگر
تفسیرها تفسیرهای مکانیک کوانتومی خودآگاهی باعث فروریزش تابع موج Consistent histories تفسیر کپنهاگی مکانیک بوهمی Ensemble تئوری متغیر پنهان دنیاهای چندگانه Objective collapse Pondicherry منطق کوانتومی Relational مکانیک کوانتومی تصادفی Transactional
عناوین پیشرفته آشوب کوانتومی نظریه میدان‌های کوانتومی نظریه اطلاعات کوانتومی نظریه پراکندگی Fractional quantum mechanics
دانشمندان بل بلاکت بوگولیوبوف بوهم بور باردین برن بوز لویی دوبروی آرتور هالی کامپتون لئون نیل کوپر پل دیراک فریمن دایسون کلینتون دیویسون دوارته پیتر دبای ارنفست آلبرت اینشتین هیو اورت فوک انریکو فرمی ریچارد فاینمن گوستاو هرتز ورنر کارل هایزنبرگ داوید هیلبرت جردن کلاوس فون کلیتسینگ پولیکارپ کوش کارمرز جان فون نویمان ولفگانگ پائولی ویلیس اوژن لمب ماکس فون لائو رابرت لافلین هنری موزلی رابرت میلیکان هایک کامرلینگ اونس ماکس پلانک سی وی رامان یوهانس ریدبرگ عبدالسلام سیمونز اروین شرودینگر هورست لودویگ اشتورمر ویلیام شاکلی جان رابرت شریفر کلیفورد گلنوود شال آرنولد زومرفلد جرج پاجت تامسون دانیل چی تسوئی سین‌ایترو تومونوجا هرمان ویل وارد ویلهلم وین یوجین ویگنر پیتر زیمان تسایلینگر
ن ب و

مکانیک کوانتومی (به انگلیسی: Quantum mechanics) شاخه‌ای بنیادی از فیزیک نظری است که با پدیده‌های فیزیکی در مقیاس میکروسکوپی سر و کار دارد. در این مقیاس، کُنِش‌های فیزیکی در حد و اندازهٔ ثابت پلانک هستند. مقدار عددی ثابت پلانک نیز بسیار کوچک و برابر است با ۶٫۶۲۶x10^-۳۴. ژول-ثانیه یا 15-^10×4.14 الکترون ولت-ثانیه.

بنیادی‌ترین تفاوت مکانیک کوانتومی با مکانیک کلاسیک در این است که مکانیک کوانتومی توصیفی سازگار با آزمایش‌ها از ذرات در اندازه‌های اتمی و زیراتمی در اختیار می‌نهد، در حالی که مکانیک کلاسیک در قلمرو میکروسکوپی(فیزیک در ابعاد هسته)و سرعت های نزدیک نور به نتایج نادرست می‌انجامد. در حقیقت، مکانیک کوانتومی بنیادی‌تر از مکانیک نیوتونی و الکترومغناطیس کلاسیک است؛ زیرا در مقیاس‌های اتمی و زیراتمی که این نظریه‌ها با شکست مواجه می‌شوند، با دقت زیادی بسیاری از پدیده‌ها را توصیف می‌کند. مکانیک کوانتومی به همراه نسبیت پایه‌های فیزیک نوین را تشکیل می‌دهند.

مکانیک کوانتومی یا نظریهٔ کوانتومی شامل نظریه‌ای دربارهٔ ماده و تابش الکترومغناطیسی و برهمکنش میان ماده و این تابش است.^[۲]

آشنایی

واژهٔ لاتین کوانتوم در مکانیک کوانتومی از این‌جا می‌آید که این نظریه به بعضی از کمیت‌های فیزیکی (مانند انرژی اتم ساکن) در شرایط خاص مقدارهای گسسته‌ای نسبت می‌دهد. پایه‌های مکانیک کوانتومی در نیمهٔ اول قرن بیستم به کوشش ورنر هایزنبرگ، ماکس پلانک، آلبرت اینشتین، لویی دو بروی، نیلز بور، اروین شرودینگر، ماکس برن، جان فون نویمان، پل دیراک، ولفگانگ پاولی، ریچارد فاینمن ودیگران ساخته شد. بعضی از جنبه‌های بنیادی این نظریه هنوز هم در حال پیشرفت است.

در ابتدای قرن بیستم، کشفیات و تجربه‌های زیادی نشان می‌دادند که در مقیاس اتمی نظریه‌های کلاسیک نمی‌توانند توصیف کاملی از پدیده‌ها ارائه دهند. وجود همین نارسایی‌ها موجب نخستین ایده‌ها و ابداع‌ها در مسیر ایجاد نظریهٔ کوانتومی شد. نمونهٔ مشهور این بود که اگر قرار است مکانیک نیوتنی و الکترومغناطیس کلاسیک بر رفتار اتم حاکم باشند، الکترون‌ها باید به سرعت به سمت هستهٔ اتم حرکت و بر روی آن سقوط می‌کردند و در نتیجه اتم‌ها ناپایدار می‌شدند، ولی در دنیای واقعی الکترون‌ها در نواحی خاصی دور اتم‌ها باقی می‌مانند و چنین سقوطی مشاهده نمی‌شود. اولین راه حل این تناقض را نیلز بور با پیشنهاد فرضیه‌اش دایر بر وجود مدارهای مانا مطرح کرد که از قضا در توصیف طیف اتم هیدروژن موفق هم بود.

پدیدهٔ دیگری که در این مسیر جلب توجه می‌کرد رفتار امواج الکترومغناطیسی مانند نور در برهمکنش با ماده بود. ماکس پلانک در سال ۱۹۰۰ هنگام مطالعهٔ تابش جسم سیاه پیشنهاد کرد که برای توصیف صحیح مسئلهٔ تابش جسم سیاه می‌توان انرژی این امواج را به شکل بسته‌های کوچکی (کوانتوم) در نظر گرفت. آلبرت اینشتین از این فکر بهره برد و نشان داد که امواجی مثل نور را می‌توان با ذره‌ای به نام فوتون که انرژی‌اش به بسامد موج بستگی دارد توصیف کرد:

${\displaystyle E=h\nu \ }$

در ادامه، دوبروی توصیف موج‌گونهٔ حرکت ذرات را مطرح کرد که اکنون به دوگانگی موج-ذره موسوم است. برطبق آن، ذرات دو نوع رفتار (موجی و ذره‌ای) را از خود نشان می‌دهند. نظریه کوانتومی که در ابتدا با کشف نظری فوتون به کوشش ماکس پلانک در ۱۹۰۰ آغاز شد و با کارهای نیلز بور به پیشرفت چشم‌گیری رسید هنوز نظریهٔ منسجمی نبود، بلکه مجموعه‌ای بود از فرضیات و اصول و قضایا و دستورالعمل‌های محاسبه‌ای. در واقع، هر مسئلهٔ کوانتومی را ابتدا به روش مکانیک کلاسیک حل می‌کردند و سپس جواب را یا با شرایط کوانتومی وفق می‌داند یا با اصل تطابق به زبان کوانتومی درمی‌آورند. به عبارت دیگر، تلاش‌ها بیشتر بر اساس حدس‌های زیرکانه بود تا استدلال‌های منطقی.

تلاش‌ها برای تبیین تناقضات و ابداع رهیافت‌های جدید به تکوین ساختار جدیدی موسوم به مکانیک کوانتومی انجامید که دو فرمول‌بندی جداگانه دارد (بعداً معلوم شد که این دو هم‌ارزند): مکانیک ماتریسی (عمدتاً به کوشش هایزنبرگ) و مکانیک موجی (بیشتر به همت شرودینگر). به‌طور مثال، ایدهٔ توصیف ذرات با امواج مولّد ابداع مفهوم بسته‌های موج شد، و در نهایت نیز تلاش برای یافتن معادلات حاکم بر تحول زمانی این بسته‌های موج به معادلهٔ موج یا معادلهٔ شرودینگر منتهی شد.

در توصیف شرودینگر از مکانیک کوانتومی، حالت هر سیستم فیزیکی در هر لحظه با تابع موج مختلطی توصیف می‌شود که از حل معادلهٔ شرودینگر به دست می‌آید:

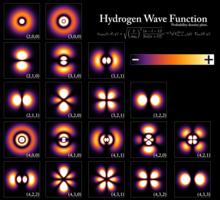
چون تابع موج کمیتی مختلط است، خود مستقیماً مُبیّن کمیتی فیزیکی نیست، اما با استفاده از این تابع می‌توان احتمال به دست آمدن مقادیر مختلف حاصل از اندازه‌گیری هر کمیت فیزیکی را پیش‌بینی کرد. در حقیقت، این احتمال با ضریبی از مربع قدرمطلق تابع موج، که کمیتی حقیقی است، برابر است. با دانستن تابع موج مثلاً می‌توان احتمال یافتن الکترون در ناحیهٔ خاصی در اطراف هسته در یک زمان مشخص یا احتمال به دست آمدن مقدار خاصی برای کمیت تکانهٔ زاویه‌ای سیستم را محاسبه کرد. یا مثلاً به کمک تابع موج و توزیع احتمال به‌دست آمده از آن می‌توان محتمل‌ترین مکان (یا مکان‌های) حضور ذره در فضا را یافت (در مورد الکترون‌های اتم گاهی به آن اُربیتال می‌گویند). البته معنی این حرف این نیست که الکترون در تمام ناحیه پخش شده‌است، بلکه الکترون در یک ناحیه از فضا یا هست یا نیست.

در مکانیک کلاسیک پیش‌بینی تحول زمانی مقادیر کمیت‌ها و اندازه‌گیری مقادیر کمیت‌ها در نظریه با هر دقت دلخواه ممکن است و تنها محدودیتِ موجود خطای متعارف آزمایش و آزمایشگر یا فقدان داده‌های اولیه کافی است. اما در مکانیک کوانتومی فرایند اندازه‌گیری محدودیتی ذاتی به همراه خود دارد. در واقع، نمی‌توان کمیت‌هایی مانند مکان و تکانه (کمیت‌های مزدوج) را هم‌زمان و با هر دقت دلخواه اندازه‌گیری کرد. اندازه‌گیری دقیق‌تر هر یک از این کمیت‌ها منجر به از دست رفتن هرچه بیشتر داده‌های مربوط به کمیت دیگر می‌شود. این مفهوم، که به اصل عدم قطعیت هایزنبرگ مشهور است، از مفاهیم بسیار مهم در مکانیک کوانتومی است و با مفهوم بنیادین «تأثیر فرایند اندازه‌گیری در حالت سیستم»، که از ابداعات اختصاصی مکانیک کوانتومی (در برابر مکانیک کلاسیک است)، همبسته است.

توصیف مکانیک کوانتومی از رفتار سامانه‌های فیزیکی اهمیت زیادی دارد، و بسیاری از شاخه‌های دیگر فیزیک و شیمی از مکانیک کوانتومی در چهارچوب نقش خود استفاده می‌کنند. از جملهٔ این شاخه‌ها باید اشاره کرد به فیزیک مادهٔ چگال، فیزیک حالت جامد، فیزیک اتمی، فیزیک مولکولی، شیمی محاسباتی، شیمی کوانتومی، فیزیک ذرات بنیادی، فیزیک هسته‌ای. مکانیک کوانتومی علاوه بر اینکه دنیای ذرات بسیار ریز را توصیف می‌کند، برای توضیح برخی از پدیده‌های بزرگ‌مقیاس (ماکروسکوپیک) مانند ابررسانایی و ابرشارگی هم کاربرد دارد. همچنین، کاربردهای وسیعی در حوزه فناوری‌های کاربردی بر مفاهیم و دستاوردهای مکانیک کوانتومی استوارند.

مکتب‌های فکری مکانیک کوانتومی

نظریه‌های گوناگونی دربارهٔ مسئلهٔ اندازه‌گیری در مکانیک کوانتومی مطرح شده‌است. از این میان، سه دیدگاه شایان ذکرند: دیدگاه واقع‌گرایانه که اینشتین طرفدار آن بود، دیدگاه سنتی که به تفسیر کپنهاگی هم معروف است و نیلز بور از آن حمایت می‌کرد، دیدگاه ندانم‌گرایانه یا آگنوستیک که طرفداران آن از اظهارنظر به‌طور کلی خودداری می‌کردند.^[۳]

مکانیک کوانتومی و فیزیک کلاسیک

آثار و پدیده‌هایی که در مکانیک کوانتومی و نسبیت پیش‌بینی می‌شوند به ترتیب فقط برای اجسام بسیار ریز و در سرعت‌های بسیار بالا آشکار می‌شوند. تقریباً همهٔ پدیده‌هایی که انسان در زندگی روزمره با آن‌ها سروکار دارد با دقت بسیار خوبی با فیزیک نیوتنی پیش‌بینی‌پذیر است.

در ابعاد بسیار کوچک ماده (مثلاً در حد نانومتر) یا در انرژی‌های بسیار پایین، مکانیک کوانتومی اثرهایی را پیش‌بینی می‌کند که فیزیک کلاسیک از پیش‌بینی آن ناتوان است، ولی اگر ابعاد ماده یا میزان انرژی را افزایش دهیم، به حدی می‌رسیم که می‌توانیم قوانین فیزیک کلاسیک را بدون اینکه خطای فاحشی مرتکب شویم برای توصیف پدیده‌ها به کار ببریم. به این «حد» که در آن قوانین فیزیک کلاسیک را (که معمولاً ساده‌ترند) می‌توان به جای مکانیک کوانتومی در توصیف دقیقی از پدیده‌ها به کار برد حد کلاسیک گفته می‌شود.

کوشش برای نظریهٔ وحدت‌یافته

وقتی می‌خواهیم مکانیک کوانتومی را با نظریهٔ نسبیت عام (که توصیف‌گر فضا-زمان در حضور گرانش است) ترکیب کنیم، به ناسازگاری‌هایی برمی‌خوریم که این کار را ناممکن می‌کند. حل این ناسازگاری‌ها هدف بزرگ فیزیکدانان قرن‌های بیستم و بیست‌ویکم است. فیزیکدانان بزرگی همچون استیون هاوکینگ در راه رسیدن به نظریهٔ وحدت‌یافتهٔ نهایی تلاش می‌کردند؛ نظریه‌ای که نه تنها مدل‌های مختلف فیزیک زیراتمی را یکی کند، بلکه چهار نیروی بنیادی طبیعت (نیروی قوی، نیروی ضعیف، الکترومغناطیس و گرانش) را نیز به شکل جلوه‌های مختلفی از یک نیرو یا پدیده نشان دهد.

مایعات اسپین کوانتومی

مایعات اسپین کوانتومی یکی از درهم‌تنیده‌ترین حالت‌های کوانتومی هستند که تا به امروز تصور شده‌اند و خواص آن‌ها در کاربردهایی کلیدی است که دانشمندان می‌گویند می‌توانند فناوری‌های کوانتومی را منجنیق کنند. علیرغم جستجوی ۵۰ ساله برای آنها و نظریه های متعددی که به وجود آنها اشاره می کند، هیچ کس تا به حال شاهد قطعی این وضعیت ماده را ندیده است. در واقع، محققان به دلیل دشواری اندازه‌گیری مستقیم درهم تنیدگی کوانتومی، ممکن است هرگز آن شواهد را نبینند، پدیده‌ای که آلبرت انیشتین آن را «عمل شبح‌آمیز از راه دور» نامیده است. اینجاست که دو اتم به هم متصل می‌شوند و می‌توانند اطلاعات را بدون توجه به اینکه چقدر از هم دور باشند، مبادله کنند.

مکانیک کوانتومی و زیست‌شناسی

تحقیقات چند مؤسسه در آمریکا و هلند نشان داده‌است که بسیاری از فرایندهای زیستی از مکانیک کوانتومی بهره می‌برند. قبلاً تصور می‌شد فتوسنتز گیاهان فرایندی بر پایهٔ زیست‌شیمی است، امّا تحقیقات پروفسور فلمینگ و همکارانش در دانشگاه برکلی و دانشگاه واشینگتن در سنت‌لوئیس به کشف مرحله‌ای کلیدی از فرایند فتوسنتز منجر شده که بر مکانیک کوانتومی استوار است. همچنین، پژوهش‌های کریستوفر آلتمن، پژوهشگری از مؤسسه دانش نانوی کاولی در هلند، حاکی از آن است که نحوهٔ کارکرد سلول‌های عصبی خصوصاً در مغز، که تا مدت‌ها فرایندی بر پایهٔ فعالیت‌های الکتریکی و زیست‌شیمی پنداشته می‌شد و محل بحث ساختارگرایان و ماده‌باوران و زیست‌شناسان بود، شامل سیستم‌های کوانتومی بسیاری است. این پژوهش‌ها نشان می‌دهد که سلول عصبی حلزون دریایی می‌تواند از نیروهای کوانتومی برای پردازش اطلاعات استفاده کند. در انسان نیز فیزیک کوانتومی احتمالاً در فرایند تفکر دخیل است.^[۴]

جستارهای وابسته

• نظریه عمل‌گرها
• شیمی کوانتوم
• تونل‌زنی کوانتومی
• اصل عدم قطعیت
• فیزیک امواج
• مکانیک کلاسیک
• نظریه میدان‌های کوانتومی
• نظریه آشوب
• کوانتش

منابع

[[۱]]

پیوند به بیرون

• J. O'Connor and E. F. Robertson: A history of quantum mechanics.
• Introduction to Quantum Theory at Quantiki.
• Quantum Physics Made Relatively Simple: three video lectures by Hans Bethe

• [[۲]]

در ویکی‌انبار پرونده‌هایی دربارهٔ مکانیک کوانتومی موجود است.