Toisen asteen yhtälö

Toisen asteen yhtälö on polynomiyhtälö, jonka normaalimuoto on ${\displaystyle ax^{2}+bx+c=0,\,\!}$ kun ${\displaystyle a\not =0}$.

Kun ${\displaystyle a>0}$, on kuvaaja ylöspäin aukeava paraabeli, ja negatiivisilla arvoilla vastaavasti alaspäin aukeava.

Toisen asteen yhtälön ratkaisukaava on kaava, jolla toisen asteen yhtälö voidaan ratkaista. Kaavan mukaan yhtälön ratkaisut ovat:

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}{2a}$.

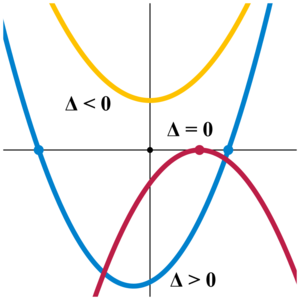
Tämä kaava pätee, olivatpa kertoimet a, b ja c reaali- tai kompleksilukuja. Jos ne ovat reaalilukuja, juurten luonne riippuu diskriminantin ${\displaystyle D=b^{2}-4ac}$ arvosta seuraavasti:

jos ${\displaystyle D>0\,\!}$, yhtälöllä on kaksi erisuurta reaalista juurta ${\displaystyle x_{1}\,\!}$ ja ${\displaystyle x_{2}\,\!}$

jos ${\displaystyle D=0\,\!}$, yhtälöllä on kaksoisjuuri ${\displaystyle x_{1,2}\,\!}$ eli kaksi yhtäsuurta reaalilukujuurta

jos ${\displaystyle D<0\,\!}$, yhtälöllä ei ole yhtään reaalilukujuurta, mutta on kaksi kompleksista juurta ${\displaystyle {\frac {-b}{2a}\pm {\frac {\sqrt {4ac-b^{2}{2a}i}$, jotka ovat toistensa liittoluvut.

Ratkaisukaavan johtamisessa halutaan ratkaista yleinen toisen asteen yhtälö

${\displaystyle ax^{2}+bx+c=0\,\!}$.

Aloitetaan siirtämällä vakiotermi:

${\displaystyle {\begin{aligned}ax^{2}+bx&=-c\end{aligned}$.

Saadun yhtälön vasen puoli pyritään täydentämään neliöksi. Aluksi kerrotaan termillä ${\displaystyle 4a}$.

${\displaystyle 4a^{2}x^{2}+4abx=-4ac\,\!}$

Nyt lisäämällä yhtälön molemmille puolille ${\displaystyle b^{2}$ saadaan binomin neliön muistikaavaa soveltamalla

${\displaystyle {\begin{aligned}4a^{2}x^{2}+4abx+b^{2}&=b^{2}-4ac\\(2ax+b)^{2}&=b^{2}-4ac\\2ax+b&=\pm {\sqrt {b^{2}-4ac}\\2ax&=-b\pm {\sqrt {b^{2}-4ac}\end{aligned}$

ja lopulta

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}{2a}$.

Ratkaisukaavan johtamisella on pyritty esittämään toisen asteen yhtälön ratkaisu helposti hallittavassa muodossa, vaikka sinänsä tarvittava matematiikka ei olekaan merkittävästi vaikeampaa kuin ensimmäisen asteen yhtälön tapauksessa.

${\displaystyle x^{2}+px+q=0\Leftrightarrow x=-{\frac {p}{2}\pm {\sqrt {\bigg (}{\frac {p}{2}{\bigg )}^{2}-q}$

Toisen asteen yhtälön ratkaisukaavasta voidaan yhtälön ${\displaystyle ax^{2}+bx+c=0}$ juurten ${\displaystyle x_{1}$ ja ${\displaystyle x_{2}$ summalle ja tulolle johtaa lausekkeet (Vietan kaavat):

• ${\displaystyle x_{1}+x_{2}=-{\frac {b}{a}\,}$
• ${\displaystyle x_{1}x_{2}={\frac {c}{a}\,}$.

Mikäli ${\displaystyle a=1}$, saadaan juurten summa ja tulo suoraan yhtälöstä yksinkertaisesti:

• ${\displaystyle x_{1}+x_{2}=-b\,}$
• ${\displaystyle x_{1}x_{2}=c\,}$.

• Seppänen, Raimo; Tiihonen, Seppo; Wuolijoki, Hilkka: ”Matematiikka: Kaavoja ja määritelmiä”, Maol-taulukot, s. 22. Helsinki: Kustannusosakeyhtiö Otava, 1991. ISBN 951-1-16053-2.