Cilindro
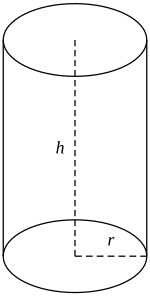

Xeometricamente, un cilindro é unha superficie das denominadas cuádricas formada polo desprazamento paralelo dunha recta chamada xeratriz ao longo dunha curva plana, que pode ser pechada ou aberta, denominada directriz do cilindro.
Se a directriz é un círculo e a xeratriz é perpendicular a el, entón a superficie obtida, chamada cilindro circular recto, será de revolución e terá logo todos os seus puntos situados a unha distancia fixa dunha liña recta, o eixe do cilindro. O sólido encerrado por esta superficie e por dous planos perpendiculares ao eixe tamén é chamado cilindro. Este sólido é utilizado como unha superficie Gausiana.
Na xeometría diferencial, un cilindro defínese de forma xeral como calquera superficie regrada xerada por unha familia uniparamétrica de liñas paralelas.
Clasificación
Un cilindro pode ser:
- cilindro rectangular: se o eixe do cilindro é perpendicular ás bases;
- cilindro oblicuo: se o eixe non é perpendicular ás bases;
- cilindro de revolución: se está limitado por unha superficie que xira 360° graos.
Superficie cilíndrica
A superficie cilíndrica está conformada por rectas paralelas, denominadas xeratrices, as cales conteñen os puntos dunha curva plana, denominada directriz do cilindro. A superficie lateral cilíndrica obtense mediante o xiro dunha recta arredor dun eixe.
- As superficies cilíndricas poden ser
- superficie cilíndrica de revolución: se todas as xeratrices equidistan dun eixe, paralelo a ela,
- superficie cilíndrica de non revolución: se non existe un eixe que equidiste das xeratrices.
Área da superficie cilíndrica
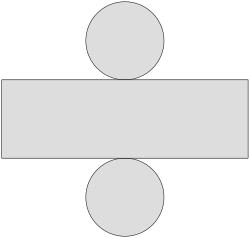
A superficie dun cilindro circular recto está conformada pola área da base, circular neste caso: A = Π r2, pero como este cilindro ten 2 bases multiplícase por 2, sendo a área total das dúas bases: Ab = 2 Π r2
Ademais, a área lateral está formada por un rectángulo de altura "h" e de largo o perímetro do círculo L = 2 Π r, polo que a área lateral é: Al = 2 Π r h
Polo tanto, a área total, ou área da superficie cilíndrica é:
A = Ab + Al
A = 2 Π r2 + 2 Π r h
A = 2 Π ( r2 + r h )
A = 2 Π r ( r + h )
Volume do cilindro
O volume dun cilindro é o produto da área da base "Ab" pola altura do cilindro "h"
O volume dun cilindro de base circular é:
V = Π r 2·h
sendo a altura do cilindro a distancia entre as bases.
Cilindro como superficie cuádrica
As seccións cónicas son de tres tipos: elipses, parábolas e hipérboles, que, sendo directrices, orixinan tres tipos de superficies cuádricas cilíndricas:



- Cilindro elíptico
Tomando como directriz unha elipse, pódese xerar unha superficie cilíndrica elíptica (que inclúe os cilindros circulares, cando os semieixes da elipse son iguais).
Nun sistema ortogonal de coordenadas, tomando como eixe z unha recta cunha dirección paralela á xeratriz, se se escolle como orixe o centro de simetría, a ecuación da superficie cilíndrica é similar á da superficie cónica correspondente.
A ecuación dun cilindro elíptico é da forma:
onde a e b son os semieixes.
- Cilindro parabólico
- Cilindro hiperbólico
Véxase tamén
Ligazóns externas
- Cilindro, en enciclopedia.us.es Arquivado 16 de xaneiro de 2013 en Wayback Machine. (en castelán)
- Representación de curvas e superficies, frrg.utn.edu.ar (en castelán)
- Livro Cônicas e Quádricas Arquivado 26 de marzo de 2013 en Wayback Machine.: Libro do Prof. Jacir J. Venturi. (en portugués)
