Esfera de Riemann

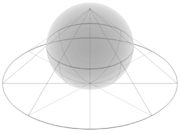	fig.1: Proxección estereográfica do plano complexo estendido sobre a "esfera de Riemann".
	fig.2: A "esfera de Riemann" pode visualizarse como o plano complexo envolto arredor dunha esfera.

En matemáticas, a esfera de Riemann (ou plano complexo estendido), chamada así en honor ao matemático do século XIX Bernhard Riemann, é unha esfera obtida do plano complexo mediante a adición dun punto do infinito. A esfera é a representación xeométrica dos números complexos estendidos, denotado como ${\displaystyle {\hat {\mathbb {C} }$ ou ${\displaystyle \mathbb {C} \cup \{\infty \}$,^[1] (véxase fig.1 e fig.2), que consiste nos números complexos ordinarios xunto co símbolo ${\displaystyle \infty \!}$ para representar o infinito.

Os números complexos estendidos son comúns na análise complexa porque permiten a división por cero nalgunha circunstancias, no sentido de facer expresións ben definidas como:

${\displaystyle 1/0=\infty }$

Por exemplo, calquera función racional sobre o plano complexo pode estenderse como unha función continua sobre a esfera de Riemann, cos polos da función racional mapeados ao infinito. Máis xeralmente, calquera función meromorfa pode pensarse como unha función continua con contradominio a esfera de Riemann.

En xeometría, a esfera de Riemann é o exemplo típico dunha superficie de Riemann e unha das variedades complexas máis simples. En xeometría proxectiva, a esfera pode pensarse como a recta proxectiva complexa ${\displaystyle \mathbb {CP} ^{1}$, o espazo proxectivo de todas as rectas complexas en ${\displaystyle \mathbb {C} ^{2}$. Como con calquera superficie de Riemann compacta, a esfera tamén pode verse como unha curva alxébrica proxectiva, sendo un exemplo fundamental da xeometría alxébrica. Tamén ten utilidade noutras disciplinas que dependen da análise e da xeometría, como pode ser a mecánica cuántica e outras ramas da física.

• Álxebra de Witt
• Punto do infinito

• Brown, James; Churchill, Ruel (1989). Complex Variables and Applications (en inglés). Nova York: McGraw-Hill. ISBN 0070109052. 
• Griffiths, Phillip; Harris, Joseph (1978). Principles of Algebraic Geometry (en inglés). John Wiley & Sons. ISBN 0-471-32792-1. 
• Penrose, Roger (2005). The Road to Reality (en inglés). Nova York: Knopf. ISBN 0-679-45443-8. 
• Rudin, Walter (1987). Real and Complex Analysis (en inglés). Nova York: McGraw-Hill. ISBN 0071002766. 
• Riemann Sphere