시차 (천문학)

시차(Parallax)는 고정된 먼 배경이 존재하는 상황에서 한 물체를 서로 다른 위치에 있는 두 관측자가 관측했을 때 발생하는 겉보기 위치의 차이 또는 변위이다. 두 관측점과 물체가 이루는 각의 반 각으로 측정한다.[1] 따라서 가까운 물체는 멀리 떨어진 물체보다 더욱 더 큰 시차를 가지게 된다. 이 성질을 이용하면 시차로서 거리를 측정할 수 있다. 천문학자들은 이러한 시차의 원리를 사용하여 천체들과 지구 사이의 거리를 측정하였다. 또한, 20세기 말 히파르코스(Hipparcos : High precision parallax collecting satellite) 인공위성은 지구와 가까운 10만개가 넘는 천체들의 시차를 측정하여 거리에 대한 정보를 알려주었다. 시차는 천문학에서 거리 측정의 기초적인 척도를 제공해 준다. 천문학에서 시차는 일주 시차, 항성 시차, 태양 시차 등이 있다. 시차는 또한 많은 광학 도구에 영향을 미친다. 대표적으로 쌍안경, 현미경 등은 관측자가 물체 관측하는 동안 약간 다른 각에서 바라보게 된다. 또, 시야와 가까운 물체는 비교적 빠르고 시야와 먼 물체는 비교적 느리게 움직이는데, 이것을 움직임 시차라 부른다. 두 개의 눈을 가진 사람을 포함한 동물들은 두 눈 사이의 거리 때문에 서로 다른 상이 맺히는데 이것을 양안 시차라 부른다. 겹치는 두 상을 인간은 깊이를 인지한다. 이것을 입체시라고 한다. 이러한 시차의 원리는 애니메이션과 컴퓨터 그래픽스, 그리고 3차원 디스플레이 기술에 적용되었다. 예를 들면, 애니메이션에서 멀티플레인 촬영기법은 시차의 원리를 사용하여 입체감과 원근감을 주는 것이다. 또한 초기의 그래픽 게임에서 입체감과 원근감을 살리기 위해 배경의 속도를 달리 하는 시차 스크롤링(parallax scrolling)기법이 적용된 사례도 종종 발견할 수 있다. 현재는 좌우의 눈이 받아들이는 상의 차이로 입체감을 느끼는 양안 시차를 이용하여 평면의 영상에 좌우의 상 차이를 만들어 주는 3차원 디스플레이 기술로도 발전하였으며, 이는 영상의 관측자가 입체감을 느끼게 하는 효과를 준다.
천문학에서의 활용
역사
일반적으로 천체는 천구 상에서 위치가 거의 변하지 않는 항성과 비교적 빠른 운동을 하고 있는 행성이나 위성 등이 있다. 행성에 포함되는 지구와 같이 움직이는 천체에 있는 관측자가 항성을 관찰할 때, 관측자의 위치에 따라 항성이 천구 상의 서로 다른 위치에서 보이게 된다. 두 위치의 차이를 시차라고 하며, 이것이 천문학에서 사용하는 시차의 개념이다.[2] 하지만, 달과 같은 위성에도 시차의 개념을 적용하기도 한다.

천문학에서 시차 문제가 중요하게 대두된 것은 지동설과 천동설의 대립이 있던 16세기 이후이다. 만약 지구가 실제로 태양의 주위를 돌고 있다면 별의 시차를 측정할 수 있어야 했고, 천문학자들은 시차를 측정하려는 시도를 한다. 하지만, 당시에 가장 정확한 관측 장비를 가지고 있었던 튀코 브라헤도 시차 측정에 실패하게 된다. 튀코는 시차 측정이 실패하려면 별들이 7,000AU이상 지구에서 떨어져 있어야 하고, 별들의 크기는 수AU에 달해야 한다고 결론지었다. 그는 이러한 사실을 받아들이지 못하였고, 천동설을 주장하게 된다.[3][4]아이작 뉴턴에 의해 지구 자전의 이론적 설명이 뒷받침되었음에도 불구하고 시차 측정의 불가능은 당시 과학계의 큰 고민거리였다.

최초로 시차 측정을 발표한 사람은 독일의 프리드리히 베셀로, 1838년에 발표하였다. 그는 백조자리 61번 별의 시차를 0.3136초로 측정하였고, 별까지의 거리가 10.6광년이라는 것을 알아내었다. 이 측정은 현대의 측정치인 11.2광년과 매우 근사한 측정치이다. 최초로 발표되지는 않았지만 최초의 시차 측정은 영국의 스콧 토머스 헨더슨에 의해 이루어졌다. 그는 현재 가장 가깝다고 알려진 별, 알파 센타우리의 시차를 측정하였다. 알파 센타우리의 시차가 1초라고 하였고, 현재 측정치가 0.76초임을 감안하면 베셀에 비해 정확하게 측정하지는 못하였다. 그러나 기술의 한계로 인해 1900년까지 61개의 별들의 시차만이 측정되었다.[5]
현대에 와서는 인공위성을 이용하여 훨씬 더 정밀하게 시차를 측정한다. 시차를 측정하는 이유는 별들까지의 거리를 직접적으로 결정할 수 있는 유일한 방법이기 때문이다. 거리를 측정함으로써 별들의 밝기, 반지름 등 많은 정보를 얻을 수 있다.[4][6] 현재 가장 정확하고 정밀하게 시차를 측정하는 위성은 1989년 유럽우주기구(European Space Agency)에서 발사된 히파르코스(Hipparchos)이다. 최초로 별들의 위치를 표시한 그리스 천문학자 히파르코스의 이름을 따온 이 위성은 4년 동안 총 118,000개의 별의 시차를 측정하였다. 히파르코스는 최대 1600광년 떨어진 별의 시차를 측정할 수 있고, 1밀리각초(milliarcsecond)의 정확도를 가진다.[5] 유럽우주기구는 더 정밀한 시차 측정을 위해 2013년에 인공위성 가이아(GAIA)를 발사할 예정이다.[7] 가이아는 지구 주위를 도는 히파르코스와 달리 태양과 지구의 중력이 평형을 이루는 지점에 위치할 예정이다. 가이아는 10마이크로각초(microarcseconds)의 정확도로 시차를 측정할 것이며, 이는 지구에서 10,000광년 떨어진 별들의 정확한 위치까지 결정할 것이다.[6]


연주 시차
지구에 있는 관측자가 어떤 별을 관측할 때, 지구의 공전에 의해서 시차가 발생한다. 연주 시차는 지구에서 관측되는 최대 시차의 절반으로 정의된다. 즉, 태양에서 관측했을 때의 별의 위치와 지구에서 관측했을 때의 별의 위치 차이가 연주 시차이다. 실제로 측정할 때에는 같은 지점에서 6개월 간격으로 각을 두 번 측정하여 계산한다.
태양에서 별까지의 거리를 d, 연주 시차를 p라고 하면, 다음과 같은 식이 성립한다.
|
|
가 매우 작으므로 로 근사하면,
|
|
여기서, 의 단위는 라디안이므로, 실제 시차 측정에서 사용하는 초(") 단위로 환산해주어야 한다. 초 단위의 시차를 이라 하면, 이므로, 이다. 따라서,
|
|
이것을 이용하여 새로운 거리 단위인 파섹(parsec, pc)을 정의하는데, 1파섹은 시차가 1초인 별의 태양으로부터의 거리다. 이며, 파섹을 사용하여 를 표현하면, 다음과 같이 간단한 식을 얻는다.[8]
|
|
일주 시차

지구에 있는 관측자가 어떤 별을 관측할 때, 지구의 공전뿐 아니라 자전에 의해서도 시차가 발생한다. 연주 시차와 비슷하게 지구 중심에서 관측되는 별의 위치와 지구 표면에서 관측했을 때의 별의 위치 차이를 일주 시차라고 한다. 일주 시차는 달이나 소행성을 제외한 다른 천체들에서는 값이 매우 작아 거의 의미가 없다.
항성 시차
과거부터 측량학자들은 시차를 이용한 삼각측량법이라는 방법으로 어떤 지점까지의 거리를 측정하였다. 측정 대상이 별(항성)인 경우, 지구로부터 별까지의 거리를 결정할 수 있으며, 이때 측정되는 시차를 항성 시차라고 부른다. 항성 시차는 일반적으로 연주 시차를 이용하여 측정되며, 연주 시차와 거리의 관계로부터 별까지의 거리를 측정한다. 위의 유도 과정에서도 볼 수 있듯이, 연주 시차를 이용하기 위해서는 별과 태양을 잇는 직선에 지구의 두 위치를 잇는 직선이 수직이 되어야 한다. 이 위치를 실제 측정 전에는 결정할 수는 없지만, 공전 궤도상에서 정 반대에 있는 두 지점에서 측정한 별의 시차는 연주 시차와 항상 같아짐을 수학적으로 유도할 수 있다.[9]시차
응용 분야
운동 시차
가까운 물체는 시야 내에서 상대적으로 빠르게 움직이고 멀리 있는 물체는 시야 내에서 상대적으로 느리게 움직이는 것처럼 보이는 현상이다. 입체시를 느끼는 요인 중 단안에 의한 입체감에 해당되며 경험적 요인으로 발생하는 입체감이다.[10]
양안 시차
보통 사람의 오른쪽 눈과 왼쪽 눈은 약 6.5센티미터 떨어져 있다. 따라서 오른쪽 눈이 보는 상과 왼쪽 눈이 보는 상에는 시차가 생기게 된다. 이를 양안 시차라고 한다. 우리의 좌안과 우안은 각각의 망막에 맺힌 서로 다른 2차원 상을 보게 되는데, 이 두 상이 망막을 통해 뇌로 전달되면 뇌는 이 상을 융합하여 인간이 3차원적인 깊이감을 느끼게 해 준다.[10]
애니메이션에서의 활용

미국의 월트 디즈니 컴퍼니는 1937년 만화영화 백설공주와 일곱 난쟁이를 제작하였다. 이 때 만화영화를 보는 관객에게 원근감을 주기 위해 시차를 이용한 멀티플레인 촬영기법을 사용하였다.[11] 멀티플레인 촬영기법은 하나의 화면을 이루게 될 배경 소재들을 여러 평면에 담아 각각 거리를 두고 동일 수직선상에 일치하게 배치시킴으로써 카메라 촬영 시 입체감을 더해주는 애니메이션 촬영기법이다. 피사체는 투명한 재질로 만들어진 패널에 그려지며 화면 속의 배경과 동시에 촬영된다. 이 때 각 평면과 카메라 사이의 거리를 평면을 전진 및 후퇴시킴으로써 조절할 수 있으며, 이 운동에 의해 움직임 시차가 발생하여 원근감을 만들어 줄 수 있게 된다. 이 기법은 주로 피사체를 강조하고자 할 때 사용한다.[12]
컴퓨터 그래픽스에서의 활용

주로 고전 비디오 게임과 같은 그래픽 활용 초기단계에서, 그래픽을 보는 사용자로 하여금 입체감을 불어넣어 주기 위해 시차 스크롤링(parallax scrolling) 기법을 사용하는 것을 볼 수 있다.[13] 이 기술은 앞서 언급된 여러 층으로 구분하여 시차를 내는 아이디어는 월트 디즈니사의 멀티플레인 촬영 기법에서 유래되었다.[14] 시차 스크롤링이란, 화면에 그려질 그래픽을 원근에 따라 몇 가지 층(layer)으로 구분하여 각 층에 해당하는 그래픽을 구현하고 가깝고 먼 정도에 따라 독립적인 이동속력을 가지게 하여 원근감을 주는 그래픽 기법이다. 이 경우, 층간의 움직임 시차가 발생하여 특정한 층의 그래픽이 같은 화면에서 더 깊이 존재하는 것 같은 느낌을 줌으로서 해당 그래픽이 더 멀리 있는 것 같은 느낌이 들게 된다. 최근에는 웹사이트의 디자인에도 자바스크립트 등의 방법을 통하여 시차 스크롤링을 구현시켜 적용되고 있으며, 웹사이트 내에서 스크롤 시 주요 대상과 배경 템플릿의 움직이는 속도를 달리하는 원리를 이용하여 시차 스크롤링 효과를 나타낸다. [15] 이외 스마트폰에서 안드로이드 운영체제의 기본 배경화면에서 시차 스크롤링을 찾아볼 수 있다.[16]
양안 시차를 이용한 3차원 디스플레이 기술
양안 시차는 좌우의 눈이 받아들이는 상의 차이에 따라 인간으로 하여금 입체감을 느끼게 하는 요소이다. 따라서 양안 시차의 근본적 원리인 좌우의 상 차이를 인위적으로 만들어 주면 평면에 나타나는 영상에서 어느 정도 깊이감이 인지될 수 있도록 할 수 있으며, 인간의 눈은 이를 입체로 인식하게 된다. 이것을 3차원 디스플레이 기술이라고 한다. 이 기술은 크게 안경식 3차원 디스플레이, 무안경식 3차원 디스플레이로 분류된다.[17]

안경식 3차원 디스플레이
안경식 3차원 디스플레이의 기본적 개념은 특수한 안경을 사용하여 왼쪽 눈과 오른쪽 눈이 서로 다른 영상을 보게 하는 것이다. 이들은 모두 양안 시차를 이용한다. 안경식 3차원 디스플레이의 간단한 예로는 적청 안경을 통한 3차원 디스플레이가 있다. 왼쪽 눈을 통해서 보여지는 영상을 적색으로, 오른쪽 눈을 통해서 보여지는 영상을 청색으로 처리하여 이를 하나의 영상으로 합친 것을 왼쪽이 적색, 오른쪽이 청색으로 된 특수한 안경을 통해 보면 양안 시차에 의해 평면에 비쳐진 영상이 입체적으로 보여지게 된다. 적청 안경에 의한 방법이 개발된 이후 편광 안경을 쓰는 방식이나 좌안과 우안을 순차적으로 개폐하는 액정 셔터 안경 등이 개발되었으나 근본적으로 안경을 써야 한다는 불편함이 있다. 하지만 기술적으로 비교적 단순하며 큰 입체감을 갖는 동영상을 재생하는데 용이하여, 3차원 영화에 적용되는 등 상업화가 상당히 이루어져 있는 편이다.[17]
무안경식 3차원 디스플레이 기술
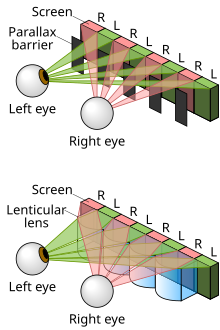
무안경식 3차원 디스플레이의 경우 양안 시차를 이용하는 방법은 시차 장벽을 이용하는 방식이 있다. 이것의 원리는 영상의 디스플레이 패널의 일정 거리 앞에 장벽의 역할을 하는 주기적인 슬릿을 설치하여 관측자의 좌안과 우안이 서로 다른 픽셀에 해당하는 영역을 보이게 만드는 것이다. 이로 인해 좌안과 우안은 서로 다른 영상을 보게 되며 관측자는 양안 시차에 의해 입체감을 느끼게 된다. 시차 장벽 대신 원통형의 렌즈의 배열로서 좌안과 우안이 서로 다른 픽셀을 보게 하는 렌티큘라 렌즈를 이용해도 같은 효과를 얻는다. 양안 시차를 이용한 무안경식 3차원 디스플레이 역시 기술의 실용성이 높고 상용화가 비교적 간단하여 닌텐도3DS와 같은 전자기기에 활용되고 있다.[18] 다만 관측자의 위치가 고정되어 있을 때 3차원 효과가 가장 잘 나타나며 지정된 위치를 벗어나게 되는 경우 올바른 3차원 영상을 보기 힘들다는 단점이 있다.[17]
같이 보기
각주
- ↑ 《Shorter Oxford English Dictionary》. 1968.
- ↑ Seeds, Michael A. (2019). 《Foundations of Astronomy》.6ed
- ↑ 《Astronomy, journey to the cosmic frontier》. 이름 목록에서
|이름1=이(가) 있지만|성1=이(가) 없음 (도움말)3ed - ↑ 가 나 그리빈, 존. 《사람이 알아야 할 모든 것, 과학》.p70-71
- ↑ 가 나 그리빈, 존. 《사람이 알아야 할 모든 것, 과학》.p684-685
- ↑ 가 나 Zeilik, Michael (1998). 《Introductory Astronomy & Astrophysics》. Saunders College Pub. ISBN 0-03-031697-9, 9780030316975
|isbn=값 확인 필요: invalid character (도움말). - ↑ “인공위성 가이아”. 2008년 3월 17일에 원본 문서에서 보존된 문서. 2012년 11월 17일에 확인함.
- ↑ 《현대천체물리학 Part I 천문학 입문과 태양계, 2ed》. 이름 목록에서
|이름1=이(가) 있지만|성1=이(가) 없음 (도움말)p70-72 - ↑ 《태양계 천문학》. 이름 목록에서
|이름1=이(가) 있지만|성1=이(가) 없음 (도움말)p73-74 - ↑ 가 나 광운대학교 이승현. “3D 입체영상의 기초(원리)”.[깨진 링크(과거 내용 찾기)]
- ↑ “백설공주와 일곱 난쟁이(네이버 지식백과)”.
- ↑ 윤남석. “2D 애니메이션에 있어서 3D CG 기술의 적용 방안 연구 : 쉐이딩 렌더링과 이미지 매핑을 중심으로(석사논문)”.
- ↑ “고전 게임의 시차 스크롤링”. 2011년 12월 26일에 원본 문서에서 보존된 문서. 2012년 11월 17일에 확인함.
- ↑ “The art of parallax scrolling” (PDF). 2009년 10월 7일에 원본 문서 (PDF)에서 보존된 문서. 2009년 7월 6일에 확인함. August 2007
- ↑ “웹페이지의 시차 스크롤링”. 2012년 11월 15일에 원본 문서에서 보존된 문서. 2012년 11월 17일에 확인함.
시차 스크롤링의 원리와 웹페이지에서의 적용
- ↑ “안드로이드 운영체제의 시차 스크롤링”. 2012년 6월 29일에 원본 문서에서 보존된 문서. 2012년 11월 17일에 확인함.
- ↑ 가 나 다 박재형 (2009). 《광학과 기술 13권 1호》. p.22-27
- ↑ 닌텐도3DS의 사양(일본어)










