Paralaks

Ilustrasi ringkas tentang paralaks objek dengan latar belakang yang jauh disebabkan oleh peralihan perspektif. Apabila dilihat dari "Sudut Pandangan A", objek kelihatan berada di hadapan segi empat sama biru. Apabila sudut pandangan ditukar kepada "Sudut Pandangan B", objek kelihatan telah beranjak ke hadapan petak merah.
Animasi ini adalah contoh paralaks. Apabila sudut pandangan bergerak dari sisi ke sisi, objek dalam jarak kelihatan bergerak lebih perlahan daripada objek yang dekat dengan kamera. Dalam kes ini, kiub putih di hadapan kelihatan bergerak lebih pantas daripada kiub hijau di tengah-tengah latar belakang yang jauh.

Paralaks (Jawi: ‏ڤارالک‌‌س‎‎) ialah anjakan atau perbezaan dalam kedudukan ketara sesuatu objek yang dilihat sepanjang dua garis penglihatan yang berbeza dan diukur dengan sudut atau separuh sudut kecondongan antara dua garisan tersebut.[1][2] Disebabkan kedekatan, objek berdekatan menunjukkan paralaks yang lebih besar daripada objek yang lebih jauh, jadi paralaks boleh digunakan untuk menentukan jarak.

Untuk mengukur jarak yang besar dari Bumi, seperti jarak planet atau bintang, ahli astronomi menggunakan prinsip paralaks. Di sini, istilah paralaks ialah separuh sudut kecenderungan antara dua garis penglihatan ke bintang, seperti yang diperhatikan apabila Bumi berada di sisi bertentangan Matahari dalam orbitnya. [a] Jarak ini membentuk anak tangga paling rendah daripada apa yang dipanggil "tangga jarak kosmik", yang pertama dalam kaedah berturut-turut yang ahli astronomi gunakan untuk menentukan jarak ke objek angkasa, berfungsi sebagai asas untuk pengukuran jarak lain dalam astronomi membentuk anak tangga yang lebih tinggi daripada tangga.

Paralaks juga mempengaruhi instrumen optik seperti skop senapang, teropong, mikroskop dan kamera refleks kanta berkembar yang melihat objek dari sudut yang berbeza sedikit. Banyak haiwan, bersama-sama dengan manusia, mempunyai dua mata dengan medan visual bertindih yang menggunakan paralaks untuk mendapatkan persepsi kedalaman; proses ini dikenali sebagai stereopsis. Dalam penglihatan komputer kesannya digunakan untuk penglihatan stereo komputer, dan terdapat peranti yang dipanggil penentu julat paralaks yang menggunakannya untuk mencari julat, dan dalam beberapa variasi juga ketinggian kepada sasaran.

Contoh paralaks mudah setiap hari boleh dilihat pada papan pemuka kenderaan bermotor yang menggunakan meter kelajuan mekanikal gaya jarum. Apabila dilihat dari hadapan terus, kelajuan mungkin menunjukkan tepat 60, tetapi apabila dilihat dari tempat duduk penumpang, jarum mungkin kelihatan menunjukkan kelajuan yang sedikit berbeza disebabkan oleh sudut pandangan digabungkan dengan anjakan jarum dari satah dail berangka.

Persepsi visual

Dalam gambar ini, Matahari kelihatan di atas bahagian atas lampu jalan. Dalam pantulan di atas air, Matahari muncul sejajar dengan lampu jalan kerana imej maya terbentuk daripada kedudukan tontonan yang berbeza.

Memandangkan mata manusia dan haiwan lain berada dalam kedudukan yang berbeza di atas kepala, mereka memberikan pandangan yang berbeza secara serentak. Ini adalah asas stereopsis, proses apabila otak mengeksploitasi paralaks disebabkan oleh pandangan yang berbeza dari mata untuk mendapatkan persepsi mendalam dan menganggarkan jarak ke objek.[3]

Haiwan juga menggunakan paralaks gerakan, iaitu haiwan (atau hanya kepala) bergerak untuk mendapatkan sudut pandangan yang berbeza. Contohnya, burung merpati (yang matanya tidak mempunyai bidang pandangan yang bertindih dan oleh itu tidak boleh menggunakan stereopsis) menjengukkan kepala mereka ke atas dan ke bawah untuk melihat kedalaman.[4] Paralaks gerakan juga dieksploitasi dalam stereoskopi goyang, grafik komputer yang memberikan petunjuk mendalam melalui animasi beralih sudut pandang dan bukannya melalui penglihatan binokular.

Pengukuran jarak

Teori paralaks untuk mencari jarak laut

Paralaks timbul disebabkan oleh perubahan dalam sudut pandangan yang berlaku disebabkan oleh gerakan pemerhati, pemerhatian, atau kedua-duanya. Apa yang penting ialah pergerakan relatif. Dengan memerhati paralaks, mengukur sudut, dan menggunakan geometri, seseorang boleh menentukan jarak.

Pengukuran jarak secara paralaks ialah kes khas prinsip triangulasi, yang menyatakan bahawa seseorang boleh menyelesaikan semua sisi dan sudut dalam rangkaian segi tiga jika panjang sekurang-kurangnya satu sisi telah diukur, sebagai tambahan kepada semua sudut dalam rangkaian. Oleh itu, pengukuran yang teliti bagi panjang satu garis dasar boleh menetapkan skala keseluruhan rangkaian triangulasi. Dalam paralaks, segi tiga adalah sangat panjang dan sempit, dan dengan mengukur kedua-dua sisi terpendeknya (gerakan pemerhati) dan sudut atas kecil (sentiasa kurang daripada 1 arkasaat,[5] meninggalkan dua yang lain hampir kepada 90 darjah), panjang sisi panjangnya (dalam amalan dianggap sama) boleh ditentukan.

Dalam astronomi, dengan mengandaikan sudutnya kecil, jarak ke bintang (diukur dalam parsek) ialah salingan paralaks (diukur dalam arkasaat): Sebagai contoh, jarak ke Proxima Centauri ialah 1/0.7687 = 1.3009 parsec (4.243 ly).[6]

Di Bumi, penentu julat bertepatan atau pengintai paralaks boleh digunakan untuk mencari jarak ke sasaran. Dalam tinjauan, masalah reseksi meneroka ukuran sudut daripada garis dasar yang diketahui untuk menentukan koordinat titik yang tidak diketahui.

Astronomi

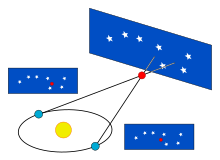
Pergerakan paralaks bintang daripada paralaks tahunan. Separuh sudut puncak ialah sudut paralaks.
Paralaks ialah sudut yang dicakup oleh garis pada suatu titik. Dalam rajah atas, Bumi dalam orbitnya menyapu sudut paralaks yang dicakup pada Matahari. Rajah bawah menunjukkan sudut yang sama disapu oleh Matahari dalam model geostatik. Rajah yang serupa boleh dilukis untuk bintang kecuali sudut paralaksnya adalah jauh lebih kecil.

Pengukuran jarak asas yang paling penting dalam astronomi datang daripada paralaks trigonometri, seperti yang digunakan dalam kaedah paralaks bintang. Semasa Bumi mengorbit Matahari, kedudukan bintang berdekatan akan kelihatan beralih sedikit terhadap latar belakang yang lebih jauh. Anjakan ini adalah sudut dalam segi tiga sama kaki, dengan 2 AU (jarak antara kedudukan melampau orbit Bumi mengelilingi Matahari) menjadikan kaki pangkal segi tiga dan jarak ke bintang ialah kaki yang sama panjang. Jumlah anjakannya agak kecil, walaupun untuk bintang terdekat, berukuran 1 arkasaat untuk objek pada 1 jarak parsek (3.26 tahun cahaya), dan selepas itu jumlah sudut semakin berkurangan apabila jarak semakin bertambah. Ahli astronomi biasanya menyatakan jarak dalam unit parsec (parallax arcseconds; paralaks arkasaat); tahun cahaya digunakan dalam media popular.

Memandangkan paralaks menjadi lebih kecil untuk jarak bintang yang lebih besar, jarak berguna boleh diukur hanya untuk bintang yang cukup dekat untuk mempunyai paralaks lebih besar daripada beberapa kali ketepatan pengukuran. Pada tahun 1990-an, sebagai contoh, misi Hipparcos memperoleh paralaks untuk lebih seratus ribu bintang dengan ketepatan kira-kira satu miliarkasaat,[7] memberikan jarak yang berguna untuk bintang ke beberapa ratus parsek jaraknya. Kamera 3 Wide Field Teleskop Angkasa Hubble berpotensi memberikan ketepatan 20 hingga 40 mikroarkasaat, membolehkan pengukuran jarak yang boleh dipercayai sehingga 5,000 parsec (16,000 ly) untuk bilangan bintang yang kecil.[8][9] Misi angkasa Gaia memberikan jarak yang sama tepat kepada kebanyakan bintang yang lebih terang daripada magnitud ke-15. Jarak boleh diukur dalam 10% sejauh Pusat Galaksi, kira-kira 30,000 tahun cahaya jauhnya. Bintang mempunyai suatu halaju jika berbanding Matahari yang menyebabkan wujudnya gerakan wajar (melintang merentasi langit) dan halaju jejarian (gerakan ke arah atau menjauhi Matahari). Yang pertama ditentukan dengan memplotkan perubahan kedudukan bintang-bintang selama bertahun-tahun, manakala yang kedua datang daripada mengukur anjakan Doppler spektrum bintang yang disebabkan oleh gerakan di sepanjang garis penglihatan. Bagi sekumpulan bintang dengan kelas spektrum yang sama dan julat magnitud yang sama, paralaks min boleh diperoleh daripada analisis statistik pergerakan yang betul berbanding dengan halaju jejarinya. Kaedah paralaks statistik ini berguna untuk mengukur jarak bintang terang melebihi 50 parsek dan bintang pembolehubah gergasi, termasuk pembolehubah Cepheids dan pembolehubah RR Lyrae.[10]

Pengukuran paralaks mungkin merupakan petunjuk penting untuk memahami tiga komponen alam semesta yang paling sukar difahami: jirim gelap, tenaga gelap dan neutrino.[11]
Pengukuran jarak bintang ketepatan Teleskop Angkasa Hubble telah dilanjutkan 10 kali lebih jauh ke dalam Bima Sakti.[12]

Pergerakan Matahari melalui ruang angkasa menyediakan garis dasar yang lebih panjang yang akan meningkatkan ketepatan ukuran paralaks, yang dikenali sebagai paralaks sekular. Untuk bintang dalam cakera Bima Sakti pula, ini sepadan dengan garis dasar purata 4 AU setahun, manakala untuk bintang halo garis dasar ialah 40 AU setahun. Selepas beberapa dekad, garis dasar boleh menjadi susunan magnitud yang lebih besar daripada garis dasar Bumi-Matahari yang biasa digunakan untuk paralaks tradisional. Walau bagaimanapun, paralaks sekular memperkenalkan tahap ketidakpastian yang lebih tinggi kerana halaju relatif bintang yang diperhatikan adalah maklumat tambahan yang tidak diketahui. Apabila digunakan pada sampel berbilang bintang, ketidakpastian boleh dikurangkan; ketidakpastian adalah berkadar songsang dengan punca kuasa dua saiz sampel.[13]

Paralaks kelompok bergerak ialah teknik yang menggunakan pergerakan bintang individu dalam kelompok bintang berdekatan untuk mencari jarak ke gugusan. Hanya kelompok terbuka yang cukup dekat untuk teknik ini berguna. Khususnya jarak yang diperoleh untuk Hyades secara sejarahnya merupakan langkah penting dalam tangga jarak.

Objek individu lain boleh mempunyai anggaran jarak asas yang dibuat untuk mereka dalam keadaan khas. Jika pengembangan awan gas seperti sisa supernova atau nebula planet boleh diperhatikan dari semasa ke semasa, maka jarak paralaks pengembangan awan itu boleh dianggarkan. Pengukuran tersebut bagaimanapun mengalami ketidakpastian dalam sisihan objek daripada sfera. Bintang binari yang merupakan binari visual dan spektroskopik juga boleh dianggarkan jaraknya dengan cara yang sama, dan tidak mengalami ketidakpastian geometri di atas. Ciri umum kaedah ini ialah pengukuran gerakan sudut digabungkan dengan pengukuran halaju mutlak (biasanya diperoleh melalui kesan Doppler). Anggaran jarak datang daripada pengiraan sejauh mana objek mesti untuk membuat halaju mutlak yang diperhatikan kelihatan dengan gerakan sudut yang diperhatikan.

Paralaks pengembangan khususnya boleh memberikan anggaran jarak asas untuk objek yang sangat jauh, kerana pancutan supernova mempunyai halaju pengembangan yang besar dan saiz yang besar (berbanding dengan bintang). Selanjutnya, ia boleh diperhatikan dengan interferometer radio yang boleh mengukur gerakan sudut yang sangat kecil. Ini bergabung untuk memberikan anggaran jarak asas kepada supernova di galaksi lain.[14] Walaupun berharga, kes sedemikian agak jarang berlaku, jadi ia berfungsi sebagai pemeriksaan ketekalan yang penting pada tangga jarak.

Metrologi

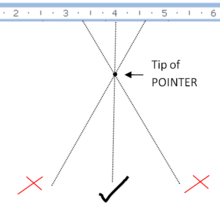
Garis penglihatan yang betul perlu digunakan untuk mengelakkan ralat paralaks.

Pengukuran yang dibuat dengan melihat kedudukan beberapa penanda berbanding sesuatu yang akan diukur adalah tertakluk kepada ralat paralaks jika penanda berada agak jauh dari objek ukuran dan tidak dilihat dari kedudukan yang betul. Contohnya, jika mengukur jarak antara dua penanda pada garisan dengan pembaris bertanda pada permukaan atasnya, ketebalan pembaris akan memisahkan tandanya daripada penanda. Jika dilihat dari kedudukan yang tidak betul-betul berserenjang dengan pembaris, kedudukan ketara akan beralih dan bacaan akan menjadi kurang tepat daripada yang mampu dilakukan oleh pembaris.

Ralat yang serupa berlaku apabila membaca kedudukan penunjuk terhadap skala dalam instrumen seperti multimeter analog. Untuk membantu pengguna mengelakkan masalah ini, skala kadang kala dicetak di atas jalur cermin sempit, dan mata pengguna diposisikan supaya penunjuk mengaburkan pantulannya, menjamin bahawa garis penglihatan pengguna adalah berserenjang dengan cermin dan oleh itu dengan skala. Kesan yang sama mengubah kelajuan dibaca pada meter kelajuan kereta oleh pemandu di hadapannya dan penumpang pergi ke tepi, nilai dibaca dari gratikul, bukan dalam sentuhan sebenar dengan paparan pada osiloskop, dsb.

Fotogrametri

Rencana utama: Fotogrametri

Apabila dilihat melalui pemapar stereo, pasangan gambar udara menawarkan kesan stereo landskap dan bangunan yang ketara. Bangunan tinggi kelihatan "terbalik" ke arah yang jauh dari tengah gambar. Pengukuran paralaks ini digunakan untuk menyimpulkan ketinggian bangunan, dengan syarat ketinggian terbang dan jarak garis dasar diketahui. Ini adalah komponen utama dalam proses fotogrametri.

Fotografi

Ralat paralaks boleh dilihat apabila mengambil foto dengan pelbagai jenis kamera, seperti kamera refleks kanta berkembar dan yang termasuk pemidang tilik (seperti kamera penilik julat). Dalam kamera sedemikian, mata melihat subjek melalui optik yang berbeza (pemidang tilik, atau kanta kedua) daripada yang digunakan untuk mengambil foto. Memandangkan pemidang tilik sering ditemui di atas kanta kamera, foto dengan ralat paralaks selalunya lebih rendah sedikit daripada yang dimaksudkan, contoh klasik ialah imej seseorang yang kepalanya terpotong. Masalah ini ditangani dalam kamera refleks kanta tunggal, apabila pemidang tilik melihat melalui kanta yang sama yang melaluinya foto diambil (dengan bantuan cermin boleh alih), dengan itu mengelakkan ralat paralaks.

Paralaks juga merupakan isu dalam jahitan imej, seperti untuk panorama.

  • Contax III rangefinder camera with macro photography setting. Because the viewfinder is on top of the lens and near the subject, goggles are fitted in front of the rangefinder and a dedicated viewfinder is installed to compensate for parallax.
    Kamera pencari jarak Contax III dengan tetapan fotografi makro. Memandangkan pemidang tilik berada di atas kanta dan berhampiran subjek, gogal dipasang di hadapan pencari jarak dan pemidang tilik khusus dipasang untuk mengimbangi paralaks.
  • Failed panoramic image due to the parallax, since the axis of rotation of the tripod is not the same as the focal point.
    Imej panorama yang gagal disebabkan oleh paralaks, kerana paksi putaran tripod tidak sama dengan titik fokus.

Pemandangan senjata

Paralaks menjejaskan peranti penampakan senjata jarak jauh dalam pelbagai cara. Pada pemandangan yang dipasang pada lengan kecil dan busur, dsb., jarak serenjang antara penglihatan dan paksi pelancar senjata (cth paksi lubang pistol)—biasanya dirujuk sebagai "ketinggian penglihatan"—boleh menyebabkan ralat sasaran yang ketara apabila menembak ke arah jarak dekat, terutamanya apabila menembak pada sasaran kecil.[15] Ralat paralaks ini diberi pampasan untuk (apabila diperlukan) melalui pengiraan yang turut mengambil pembolehubah lain seperti peluru jatuh, windage dan jarak sasaran dijangkakan.[16] Ketinggian penglihatan boleh digunakan untuk kelebihan apabila "melihat" senapang untuk kegunaan lapangan. Senapang pemburu biasa (.222 dengan pemandangan teleskopik) yang dilihat pada 75m masih berguna dari 50 hingga 200 m (55 hingga 219 yd) tanpa memerlukan pelarasan lanjut.[perlu rujukan]

Pemandangan optik

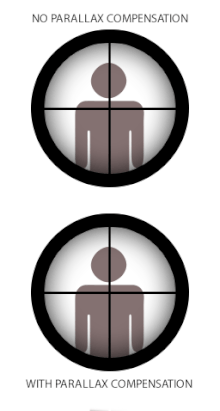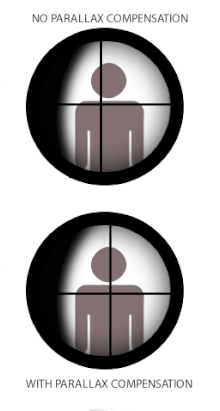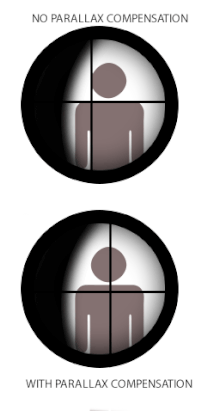
Animasi ringkas yang menunjukkan kesan pampasan paralaks dalam pemandangan teleskopik, apabila mata bergerak relatif kepada penglihatan.

Dalam sesetengah instrumen optik beretikul seperti teleskop, mikroskop atau dalam pemandangan teleskopik ("skop") yang digunakan pada lengan kecil dan teodolit, paralaks boleh menimbulkan masalah apabila retikel tidak bertepatan dengan satah fokus imej sasaran. Ini kerana apabila reticle dan sasaran tidak berada pada fokus yang sama, jarak optik sepadan yang dipancarkan melalui kanta mata juga berbeza, dan mata pengguna akan mencatatkan perbezaan paralaks antara reticle dan sasaran (setiap kali kedudukan mata berubah. ) sebagai sesaran relatif di atas satu sama lain. Istilah anjakan paralaks merujuk kepada pergerakan "terapung" jelas yang terhasil pada reticle di atas imej sasaran apabila pengguna menggerakkan kepala/matanya secara sisi (atas/bawah atau kiri/kanan) di belakang penglihatan,[17] iaitu ralat di mana reticle tidak kekal sejajar dengan paksi optik pengguna.

Tembakan artileri

Disebabkan kedudukan meriam medan atau tentera laut, setiap satu mempunyai perspektif yang sedikit berbeza mengenai sasaran berbanding dengan lokasi sistem kawalan tembakan itu sendiri. Oleh itu, apabila membidikkan senapangnya ke sasaran, sistem kawalan tembakan mesti mengimbangi paralaks untuk memastikan bahawa tembakan dari setiap senapang menumpu pada sasaran.

Seni

Beberapa karya arca Mark Renn bermain dengan paralaks, kelihatan abstrak sehingga dilihat dari sudut tertentu. Salah satu arca sedemikian ialah The Darwin Gate (gambar) di Shrewsbury, England, yang dari sudut tertentu kelihatan membentuk kubah, menurut Historic England, dalam "bentuk topi keledar Saxon dengan tingkap Norman... diilhamkan oleh ciri-ciri Gereja St Mary yang dihadiri oleh Charles Darwin semasa kecil".

tiangnya yang berasingan, masing-masing melengkung di bahagian atas
kubah ketara
Dilihat dari sudut tertentu, lengkungan tiga tiang berasingan "The Darwin Gate" kelihatan membentuk kubah

Lihat juga

  • Dispariti binokular
  • Bias Lutz–Kelker
  • Pemetaan paralaks, dalam grafik komputer
  • Penatalan paralaks, dalam grafik komputer
  • Pembiasan, prinsip yang serupa secara visual disebabkan oleh air, dsb.
  • Paralaks spektroskop
  • Triangulasi, di mana satu titik dikira berdasarkan sudutnya dari titik lain yang diketahui
  • Trigonometri
  • Xallarap

Nota

  1. ^ Pada masa lalu paralaks diurnal juga digunakan untuk mengukur jarak ke objek angkasa dalam Sistem Suria. Kaedah ini kini telah digantikan dengan teknik yang lebih tepat.
  1. ^ "Parallax". Shorter Oxford English Dictionary. 1968. Mutual inclination of two lines meeting in an angle
  2. ^ "Parallax". Oxford English Dictionary (ed. Second). 1989. Astron. Apparent displacement, or difference in the apparent position, of an object, caused by an actual change (or difference) of the position of the point of observation; spec. the angular amount of such displacement or difference of position, being the angle contained between the two straight lines drawn to the object from the two different points of view and constituting a measure of the distance of the object.
  3. ^ Steinman, Scott B.; Garzia, Ralph Philip (2000). Foundations of Binocular Vision: A Clinical perspective. McGraw-Hill Professional. m/s. 2–5. ISBN 978-0-8385-2670-5.
  4. ^ Steinman & Garzia 2000, p. 180.
  5. ^ Zeilik & Gregory 1998.
  6. ^ Benedict; G. Fritz; Chappell, D.W.; Nelan, E.; Jefferys, W.H.; Van Altena, W.; Lee, J.; Cornell, D.; Shelus, P.J. (1999). "Interferometric Astrometry of Proxima Centauri and Barnard's Star Using Hubble Space Telescope Fine Guidance Sensor 3: Detection Limits for Substellar Companions". The Astronomical Journal. 118 (2): 1086–1100. arXiv:Astro-ph/9905318. Bibcode:1999AJ....118.1086B. doi:10.1086/300975. Unknown parameter |displayauthors= ignored (bantuan)
  7. ^ Perryman, M. A. C. (1999). "The HIPPARCOS Catalogue". Astronomy and Astrophysics. 323: L49–L52. Bibcode:1997A&A...323L..49P. Unknown parameter |displayauthors= ignored (bantuan)
  8. ^ Harrington, J. D.; Villard, R. (10 April 2014). "NASA's Hubble Extends Stellar Tape Measure 10 Times Farther Into Space". NASA. Diarkibkan daripada yang asal pada 17 February 2019. Dicapai pada 17 October 2014.
  9. ^ Riess, A. G.; Casertano, S.; Anderson, J.; MacKenty, J.; Filippenko, A. V. (2014). "Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope". The Astrophysical Journal. 785 (2): 161. arXiv:1401.0484. Bibcode:2014ApJ...785..161R. doi:10.1088/0004-637X/785/2/161.
  10. ^ B., Baidyanath (2003). An Introduction to Astrophysics. PHI Learning Private Limited. ISBN 978-81-203-1121-3.
  11. ^ "Hubble finds Universe may be expanding faster than expected". Diarkibkan daripada yang asal pada 11 September 2018. Dicapai pada 3 June 2016.
  12. ^ "Hubble stretches the stellar tape measure ten times further". ESA/Hubble Images. Diarkibkan daripada yang asal pada October 30, 2017. Dicapai pada April 12, 2014.
  13. ^ Popowski, P.; Gould, A.. "Mathematics of Statistical Parallax and the Local Distance Scale". MISSING LINK. .
  14. ^ Bartel, N. (1994). "The shape, expansion rate and distance of supernova 1993J from VLBI measurements". Nature. 368 (6472): 610–613. Bibcode:1994Natur.368..610B. doi:10.1038/368610a0. Unknown parameter |displayauthors= ignored (bantuan)
  15. ^ "Ballistic Explorer Help". www.dexadine.com. Diarkibkan daripada yang asal pada 2011-09-28.
  16. ^ "Crossbows / Arrows & Bolts / Trajectory / Trajectories". www.crossbowmen.com. Diarkibkan daripada yang asal pada 2011-07-08.
  17. ^ "Setting Up An Air Rifle And Telescopic Sight For Field Target – An Instruction Manual For Beginners, page 16". Dicapai pada 2019-10-28.