중력렌즈

중력렌즈 시뮬레이션
일반 상대성이론
Spacetime curvature schematic
기초 개념
관련 현상
시공간
  • 방정식
  • 형식
방정식
형식화
고급 학설
해
학자
Portal icon 물리학 포털  분류 분류: 일반 상대성이론

중력렌즈(重力lens, 영어: gravitational lens)[1] 또는 중력렌즈 효과(重力lens效果, 영어: gravitational lensing)는 아주 먼 천체에서 나온 빛이 중간에 있는 거대한 천체에 의해 휘어져 보이는 현상을 의미한다. 일반 상대성이론의 증거 중 하나이다. 이를 통해 희미해서 관측하기 힘든 천체도 관측할 수 있다.[2][3][4]

오레스트 흐볼손(Orest D. Khvolson, 러시아어: Орест Д. Хвольсон)이 이 효과를 처음 언급하였으나, 1936년에 이에 관한 기사를 낸 아인슈타인과 관련이 있다. 프리츠 츠비키(Fritz Zwicky)는 1937년 은하무리가 중력렌즈의 역할을 한다고 주장하였다. 이 효과는 1979년까지는 증명되지 않았지만 '이중준성'이라고 불리는 'SBS 0957+561' 천체의 관측을 통해 사실임이 밝혀졌다.

설명

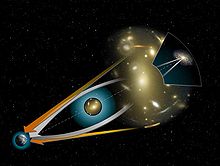
거대한 천체(중앙)로부터 멀리 떨어져 있는 빛(좌측)이 천체의 오른쪽 주변에서 원호 모양으로 휘어져 분포한다. 주황색 화살표는 광원의 겉보기 위치를 보여준다. 흰색 화살표는 광원의 실제 위치로부터 오는 빛의 경로를 보여준다.

은하단이나 블랙홀 같은 거대한 물체로부터 오는 중력은 시공간을 휘게 만들고 빛의 경로마저 휘게 만든다. 빛이 휘어져서 관찰자에게 도달하면 원래 광원의 모양은 원호의 모양으로 과장되고 왜곡되게 된다.

빛의 경로는 중력렌즈의 중심에서 가장 많이 휘어지고, 먼 곳에서는 적게 휘어진다. 이는 광학 렌즈와는 반대된다. 그 결과 중력렌즈 효과에서는 초점이 존재하지 않는다. 빛을 내는 광원과, 렌즈 효과를 내는 거대한 천체, 그리고 관찰자가 직선상에 있다고 가정한다면, 광원은 거대한 천체의 주위에 링으로 나타나게 될 것이다. 또한, 직선상에 있지 않고 어긋나 있다면 활처럼 휜 모양을 볼 수 있을 것이다. 이러한 현상은 1924년에 러시아의 물리학자 오레스트 흐볼손(Orest Chwolson)[5]에 의해 처음 언급되었고, 1936년에 아인슈타인에 의해 정량화되었으며, 종종 문헌에서 “아인슈타인 링”이라고 언급되었다. 일반적으로 중력 렌즈의 질량 분포가 복잡하고, 시공의 왜곡이 구형이 아니기 때문에, 광원은 렌즈 주위에 드문드문 흩뿌려져 있는 원호의 모양을 하게 되며, 관측자는 같은 광원이 중력 렌즈에 의해 왜곡되어 다수의 상으로 나타나는 현상을 관찰하게 된다. 관찰되는 광원의 모양과 수는, 중력 렌즈를 포함하여 관측 선상에 있는 모든 물체에 의한 중력장에 의해 결정된다.

중력렌즈효과는 가시광선 뿐만 아니라, 모든 종류의 전자기파에 동등하게 작용한다. 약한 렌즈효과는 우주배경복사에서 연구되고 있다. 강한 렌즈효과는 전파와 X-ray에서 관측되었다.

아인슈타인 링의 형태. 앞에 있는 은하의 강한 중력 렌즈 효과 때문에 멀리 떨어진 하나의 퀘이사가 은하의 네 개의 상으로 관측된다.

이론

일반상대성이론에 따르면, 질량은 중력장에 만들어진 휜 시공간이고, 그러므로 빛의 경로가 휘는 결과가 나타난다. 이 이론은 1919년에 아서 에딩턴이 일식 현상 동안 태양에 가까이 지나가는 별빛이 약간 휘는 것을 관찰함으로써 확증되었다. 거대 천체 주변에서는 주변으로부터 오는 빛이 천체 쪽으로 휘어지게 된다. 광속은 항상 일정하므로, 중력렌즈효과에서 빛의 속력은 바뀌지 않고 방향만 바뀐다. 이때 굴절각은 다음과 같다.

M은 질량, r은 영향을 받은 광원으로부터의 거리, G는 만유인력 상수, 그리고 c는 진공에서의 빛의 속도이다.

중력렌즈효과의 시뮬레이션. 블랙홀이 배경 은하를 지나가고 있다. 오른쪽 그림은 슈바르츠실트 블랙홀에 의한 중력렌즈효과의 시뮬레이션이다. 중력렌즈에 의한 이차적인 은하의 상이 실제 은하 위치의 반대쪽에서 관찰되며, 이 이차적인 상은 블랙홀의 아인슈타인 반지름(Einstein radius) 안에 위치한다. 이차적인 상의 크기는 원래의 은하 위치가 블랙홀에 가까워질수록 커진다. 원래 은하의 상과 이차적인 상 모두 겉보기 밝기는 일정하지만, 둘 사이의 각 크기는 변화한다. 이것이 멀리 떨어진 관찰자에 의해 관측되게 되면, 은하의 광도가 변화하는 것처럼 보이게 되고, 은하가 정확히 블랙홀 뒤에 위치한 경우에 은하의 겉보기 밝기가 최대로 관측된다.

중력 렌즈 효과의 종류

중력 렌즈 효과에는 세 가지 종류가 있다.:[6]

강한 렌즈효과 (Strong lensing)

쉽게 볼 수 있는 왜곡, 예를 들어 아인슈타인 링의 형태, 원호, 다중 상(multiple images).

약한 렌즈효과 (weak lensing)

광원의 왜곡이 매우 작아지고, 많은 수의 광원의 분석을 통해 겨우 몇 퍼센트의 일관성있는 왜곡이 발견된다.

많은 수의 멀리 떨어진 은하의 형태와 특성을 측정하고 측정값들의 평균치로부터 중력 렌즈효과가 얻어진다. 이 측정값으로부터 공간의 질량분포, 특히 암흑 물질 분포를 재구성할 수 있다. 은하는 본질적으로 타원형이고, 약한 중력렌즈효과는 작으므로, 아주 많은 수의 은하들이 이 연구에 사용된다. 약한 중력렌즈 효과 연구에서는 주요한 광원에 의해 발생하는 통계적 오류를 조심해야 하며, 은하의 모양을 왜곡시키는 카메라의 점 퍼짐 현상과 대기층의 영향이 주의 깊게 이해되어야 한다. 이러한 연구 결과를 통해 우주론의 매개변수들에 대한 연구가 가능하며, 특히 암흑 에너지에 대한 정보를 얻을 수 있고, 이를 통해 ΛCDM 모형을 검증/발전시키는 것이 가능하다.

미세 중력렌즈 효과 (microlensing)

중력 렌즈에 의해 겉으로 보았을 때의 모양 왜곡은 없지만, 천체로부터 관측되는 빛의 양이 변화된다. 대부분의 경우 렌즈효과를 일으키는 천체는 우리은하에 있는 주계열성이고, 배경의 광원은 우리 은하로부터 매우 멀리 떨어진 별이거나 퀘이사이다. 미소렌즈효과는 매우 약한데, 예를 들어 태양 질량의 백 만 배 이상의 은하는 수 초의 각거리 만큼 떨어진 복합된 상을 만들고, 은하단은 수 분의 각거리만큼의 분리된 상을 만든다. 두 경우 모두 우리 은하와의 거리는 매우 멀어서 파섹 이상 떨어져 있다.

적용

허블우주망원경에 관측된 실제 중력렌즈 효과(아벨 1689) - 렌즈효과에 의한 호를 볼 수 있는 확대된 이미지
암흑물질의 삼차원 분포 지도. 허블우주망원경의 약한 중력렌즈효과 측정으로부터 재구성됐다.

배경 광원에 대한 연구

중력렌즈 효과를 이용하여 “중력 망원경(gravitational telescopes)"을 고안할 수 있다. 중력망원경은 천체 뒤에 있는 빛을 모으고, 많은 미약한 천체를 밝고 크게 만들기 때문에, 이러한 천체에 대한 연구가 더욱 쉬워질 것이다. 캘리포니아공과대학의 과학자들은 허블우주망원경의 이미지를 이용하여 은하단 아벨 2218은하단에 의한 강한 중력렌즈효과를 통해 더 멀리 있는 천체를 연구하였다. 비슷하게, 미소렌즈효과는 광원이 되는 별의 추가적인 정보를 얻는 데 사용된다.[7] 만약 광원이 되는 별이 쌍성계라면, 궤도의 움직임 또한 관측될 수 있다.(xallarap 효과)

전면 렌즈효과의 연구

중력렌즈 효과를 만드는 천체 그 자체를 연구하기 위해 중력렌즈 효과를 관찰할 수 있다. 이 방법은 특히 천체의 질량을 측정하는 데 이용되며, 천체가 만드는 빛에 의한 측정과는 독립적인 관찰이므로 두 측정을 비교하는 연구가 가능하다. 또한 블랙홀과 같이 빛에 의한 관측이 되지 않는 경우에 유용하다. 미소렌즈효과를 통해 (중력렌즈 효과를 만드는) 비교적 작은 천체에 대한 정보를 얻을 수 있는데, 예를 들어 우리은하 안에 있는 MACHOs나 외계 행성(태양계저편에 행성들)의 정보를 얻을 수 있다. 태양계 밖에 있는 세 개의 행성은 이러한 방법으로 찾았으며, 지구형 행성의 발견도 기대할 수 있다. Microlensing Observations in Astrophysics(MOA) Probing Lensing Anomalies Network(PLANET)는 이와 같은 연구를 목적으로 한다.

우주의 기하학적 구조

전면에 있는 은하단에 의한 강한 중력렌즈 효과와 약한 중력렌즈 효과를 이용하면 암흑 물질의 양과 분포도 연구할 수 있다. 이를 포함하여 전면 렌즈 안에서의 질량분포가 이해된다면, 암흑 에너지와 허블상수로 기술되는 우주의 팽창 효과를 더욱 정확히 이해할 수 있다.

같이 보기

역사적 주요 논문과 참고 자료

관련 영화

각주

  1. ↑ 한국천문학회 편 천문학용어집 208쪽 좌단 26째줄
  2. ↑ 아인슈타인의 꿈, 중력렌즈로 별 질량 측정 실현. YTN. 2017년 6월 8일.
  3. ↑ 윤신영. 우주 보는 ‘중력의 눈’ 위력 확인해... 중성자별 세밀하게 밝힌 것도 의의. 동아사이언스. 2017년 10월 17일.
  4. ↑ 고든 정. (고든 정의 TECH+)본래 밝기의 30배로…역대 최고 배율 중력 렌즈 발견. 서울신문. 2018년 2월 24일.
  5. ↑ Gravity Lens - Part 2 (Great Moments in Science, ABS Science)
  6. ↑ Melia, Fulvio (2007). 《The Galactic Supermassive Black Hole》. Princeton University Press. 255–256쪽. ISBN 0-691-13129-5. 
  7. ↑ “Stellar Atmospheres”. MOA collaboration. 2010년 5월 25일에 원본 문서에서 보존된 문서. 2010년 4월 24일에 확인함. 
  8. ↑ 김형욱. 기대보단 아쉽지만, '놀란'이니까 다시 볼 수밖에 없는 영화. 오마이뉴스. 2018년 1월 26일.

기타 출처

더 읽어 보기

외부 링크

위키미디어 공용에 관련된
미디어 분류가 있습니다.