Рамнокрак триаголник
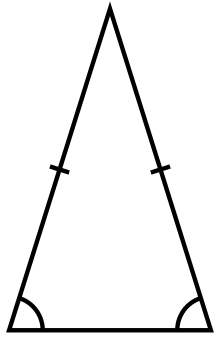
Рамнокрак триаголник Рамнокрак триаголник со вертикална оска на симетрија
Вид триаголник Рабови и темиња 3 Шлефлиев симбол ( ) ∨ { } Група на симетрија Dih2, [ ], (*), ред 2 Својства конвексен , тетивен
Рамнокрак триаголник – триаголник кој има две исти страни. Тие две еднакви страни се обележуваат со
b
{\displaystyle b\,}
латинична буква „б“) и се нарекуваат краци на рамнокракиот триаголник. Страната над која се наоѓаат краците се нарекува основа и се обележува со
a
{\displaystyle a\,}
врв на рамнокракиот триаголник.
Два агли во овој триаголник се еднакви — тоа се аглите кои лежат на основата
Висината на триаголникот е еднаква на медијаната
Висината се поклопува со бисектрисата и медијаната
Страните на триаголникот може да се пресметаат со следните формули:
a
=
2
R
sin
α
{\displaystyle a=2R\sin \alpha \,}
b
=
2
R
sin
β
{\displaystyle b=2R\sin \beta \,}
b
=
2
a
cos
α
{\displaystyle b=2a\cos \alpha \,}
a
=
b
2
cos
α
{\displaystyle a={\frac {b}{2\cos \alpha }
b
=
a
2
(
1
−
cos
β
)
{\displaystyle b=a{\sqrt {2(1-\cos \beta )}
Обемот
O
=
2
b
+
a
{\displaystyle O=2b+a\,}
O
=
2
R
(
2
sin
α
+
sin
β
)
{\displaystyle O=2R(2\sin \alpha +\sin \beta )\,}
Висината
a
{\displaystyle a\,}
b
{\displaystyle b\,}
h
a
=
b
2
−
a
2
4
{\displaystyle h_{a}={\sqrt[{}]{b^{2}-{\frac {a^{2}{4}
h
b
=
2
P
b
=
a
h
a
b
{\displaystyle h_{b}={\frac {2P}{b}={\frac {ah_{a}{b}
Плоштината
P
=
a
⋅
h
a
2
=
b
⋅
h
b
2
{\displaystyle P={\frac {a\cdot h_{a}{2}={\frac {b\cdot h_{b}{2}
P
=
1
2
b
2
sin
β
=
1
2
a
b
sin
α
{\displaystyle P={\frac {1}{2}b^{2}\sin \beta ={\frac {1}{2}ab\sin \alpha }
P
=
1
2
b
(
a
+
1
2
b
)
(
a
−
1
2
b
)
{\displaystyle P={\frac {1}{2}b{\sqrt {\left(a+{\frac {1}{2}b\right)\left(a-{\frac {1}{2}b\right)}
Херонова формула )Аглите се пресметуваат на следниот начин:
α
=
π
−
β
2
{\displaystyle \alpha ={\frac {\pi -\beta }{2}
β
=
π
−
2
α
{\displaystyle \beta =\pi -2\alpha \,}
α
=
arcsin
a
2
R
,
β
=
arcsin
b
2
R
{\displaystyle \alpha =\arcsin {\frac {a}{2R},\beta =\arcsin {\frac {b}{2R}
The article is a derivative under the Creative Commons Attribution-ShareAlike License .
A link to the original article can be found here and attribution parties here
By using this site, you agree to the Terms of Use . Gpedia ® is a registered trademark of the Cyberajah Pty Ltd









![{\displaystyle h_{a}={\sqrt[{}]{b^{2}-{\frac {a^{2}{4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c023b93c143b2c01ac44f6a826813aab30f76905)






