Círculo

Na geometria, um círculo, por vezes chamado de disco,[nota 1] é a região em um plano delimitada por uma circunferência. Um círculo é considerado fechado se contiver a circunferência que constitui seu limite, e aberto se não contiver.[8] Um círculo de raio r e centro O é geralmente denotado como C(O; r).
Etimologia
A palavra círculo deriva do grego κίρκος/κύκλος (kirkos/kuklos), que é uma metátese do grego homérico κρίκος (krikos), que significa "aro" ou "anel".[9] As origens das palavras circo e circuito estão intimamente relacionadas.
Fórmulas
Em coordenadas cartesianas, o círculo aberto de centro O(a, b) e o raio R é dado pela fórmula:[10]
enquanto o círculo fechado com o mesmo centro e raio é dado por:
Propriedades
O círculo tem simetria circular.[11]
O círculo aberto e o fechado não são topologicamente equivalentes (ou seja, não são homeomórficos), pois têm propriedades topológicas diferentes um do outro. Por exemplo, todo círculo fechado é compacto, ao passo que todo círculo aberto não é compacto.[12] Entretanto, do ponto de vista da topologia algébrica, eles compartilham muitas propriedades: ambos são contraíveis[13] e, portanto, são homotopicamente equivalentes a um único ponto. Isso implica que seus grupos fundamentais são triviais e todos os grupos de homologia são triviais, exceto o 0, que é isomórfico a Z. A característica de Euler de um ponto (e, portanto, também a de um círculo fechado ou aberto) é 1.[nota 2]
Todo mapa contínuo do círculo fechado para ele mesmo tem pelo menos um ponto fixo (não é necessário que o mapa seja bijetivo ou mesmo sobrejetivo); esse é o caso n = 2 do teorema do ponto fixo de Brouwer.[15] A afirmação é falsa para o círculo aberto:[16] considere, por exemplo, a função
que mapeia cada ponto do círculo unitário aberto para outro ponto no circulo unitário aberto à direita do ponto dado. Mas para o círculo unitário fechado, ele fixa cada ponto no semicírculo x2 + y2 = 1, x > 0.
Como uma distribuição estatística
Uma distribuição uniforme em um círculo unitário é ocasionalmente encontrada em estatística. Ela ocorre mais comumente em investigação operacional na matemática do planejamento urbano, onde pode ser usada para modelar uma população dentro de uma cidade. Outros usos podem tirar proveito do fato de ser uma distribuição para a qual é fácil calcular a probabilidade de que um determinado conjunto de desigualdades lineares seja satisfeito. (As distribuições gaussianas no plano exigem quadratura numérica).
"Um argumento engenhoso por meio de funções elementares" mostra que a distância euclidiana média entre dois pontos no círculo é 12845π ≈ 0.90541,[17] enquanto a integração direta em coordenadas polares mostra que a distância média ao quadrado é 1.
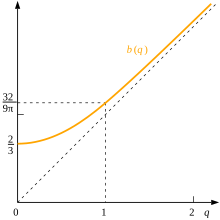
Se for dado um local arbitrário a uma distância q do centro do círculo, também é interessante determinar a distância média b(q) dos pontos na distribuição até esse local e o quadrado médio dessas distâncias. O último valor pode ser calculado diretamente como q2 + 12.
Distância média até um ponto interno arbitrário

Para encontrar a distância b(q), precisamos analisar separadamente os casos em que a localização é interna ou externa, ou seja, em que q ≶ 1, e descobrimos que em ambos os casos o resultado só pode ser expresso em termos de integrais elípticas completas.
Se considerarmos uma localização interna, nosso objetivo (olhando para o diagrama) é calcular o valor esperado de r sob uma distribuição cuja densidade é 1π para 0 ≤ r ≤ s(θ), integrando em coordenadas polares centradas no local fixo para o qual a área de uma célula é r dr dθ ; portanto
Aqui s(θ) pode ser encontrado em termos de q e θ usando a lei dos cossenos. As etapas necessárias para avaliar a integral, juntamente com várias referências, podem ser encontradas no artigo de Lew et al.;[17] o resultado é que
onde K e E são integrais elípticas completas do primeiro e segundo tipos.[18] b(0) = 23; b(1) = 329π ≈ 1.13177.
Distância média até um ponto externo arbitrário

Voltando a um local externo, podemos configurar a integral de maneira semelhante, desta vez obtendo
onde a lei dos cossenos nos diz que s+(θ) e s–(θ) são as raízes para s da equação
Portanto
Podemos substituir u = q sinθ para obter
usando integrais padrão.[19]
Portanto, novamente b(1) = 329π e também[20]
Ver também
Notas e referências
Notas
- ↑ Em inglês, o termos utilizado é disk, de forma que em alguns livros, especialmente aqueles direcionados para o ensino superior, utilizem a palavra disco para se referir à figura, como pode ser observado em Geometria euclidiana plana, de Barbosa,[1] ou em Curso de análise, de Lima.[2] No entanto, no ensino básico, a palavra utilizada é círculo, como pode ser observado nos livros didáticos das editoras FTD,[3] Editora do Brasil,[4] Edições SM,[5] e Moderna.[6][7]
- ↑ Em dimensões maiores, a característica de Euler de uma esfera fechada permanece igual a +1, mas a característica de Euler de uma esfera aberta é +1 para esferas de dimensão par e -1 para esferas de dimensão ímpar.[14]
Referências
- ↑ Barbosa, João Lucas Marques (Agosto de 1997) [1995]. Geometria Euclidiana Plana. Rio de Janeiro, RJ: Sociedade Brasileira de Matemática. p. 12. ISBN 978-85-85818-02-9.
Todo ponto C que satisfaz a desigualdade AC < r é dito estar dentro do círculo. Se, ao invés, AC > r, então C é dito estar fora do círculo. O conjunto dos pontos que estão dentro do círculo é chamado de disco de raio r e centro A.
- ↑ Lima, Elon Lages (2014). Curso de análise. Rio de Janeiro, RJ: IMPA. p. 19. ISBN 978-85-244-0375-0.
Agora consideremos o disco D de centro na origem e raio 1. Temos D = {(x, y) ∈ R2; x2 + y2 ≤ 1}.
- ↑ Giovannni Jr., José Ruy; Castrucci, Benedicto (2009). A conquista da Matemática. 8. São Paulo, SP: FTD. p. 330. ISBN 978-85-322-7013-9.
A região da circunferência com a sua região interna denomina-se círculo.
- ↑ Andrini, Álvaro; Vasconcellos, Maria José (2015). Praticando Matemática. 9. São Paulo, SP: Editora do Brasil. p. 225. ISBN 978-85-10-05898-8.
Juntando à circunferência os pontos do seu interior, obtemos um círculo.
- ↑ Chavante, Eduardo Rodrigues (2015). Convergências: Matemática. 9. São Paulo, SP: Edições SM. p. 182. ISBN 978-85-418-0967-2.
Círculo é uma figura geométrica plana correspondente à união de uma circunferência com todos os pontos do seu interior.
- ↑ Projeto Araribá: Matemática. 8. São Paulo, SP: Círculo é a região do plano formada por uma circunferência e sua região interna. 2007. p. 227. ISBN 978-85-16-05518-9
- ↑ Bianchini, Edwaldo (2018). Matemática — Bianchini. 9. São Paulo, SP: Moderna. p. 287. ISBN 978-85-16-11381-0
- ↑ Arnold, B. H. (2013), Intuitive Concepts in Elementary Topology, ISBN 9780486275765, Dover Books on Mathematics, Courier Dover Publications, p. 58.
- ↑ Liddell, Henry George; Scott, Robert. «krikos». Perseus. A Greek-English Lexicon. Cópia arquivada em 6 de novembro de 2013
- ↑ Clapham, Christopher; Nicholson, James (2014), The Concise Oxford Dictionary of Mathematics, ISBN 9780199679591, Oxford University Press, p. 138.
- ↑ Altmann, Simon L. (1992). Icons and Symmetries (em inglês). [S.l.]: Oxford University Press. ISBN 9780198555995.
disc circular symmetry.
- ↑ Maudlin, Tim (2014). New Foundations for Physical Geometry: The Theory of Linear Structures. [S.l.]: Oxford University Press. p. 339. ISBN 9780191004551.
- ↑ Cohen, Daniel E. (1989). Combinatorial Group Theory: A Topological Approach. Col: London Mathematical Society Student Texts. 14. [S.l.]: Cambridge University Press. p. 79. ISBN 9780521349369.
- ↑ Klain, Daniel A.; Rota, Gian-Carlo (1997). Introduction to Geometric Probability. Col: Lezioni Lincee. [S.l.]: Cambridge University Press. pp. 46–50
- ↑ Arnold 2013, p. 132.
- ↑ Arnold 2013, p. 135, ex. 1.
- ↑ a b Lew, John S.; Frauenthal, James C.; Keyfitz, Nathan (1978). «On the Average Distances in a Circular Disc». Society for Industrial and Applied Mathematics. SIAM Review. 20 (3): 584–592. ISSN 0036-1445
- ↑ Handbook of Mathematical Functions, 17.3.
- ↑ Gradshteyn e Ryzhik 3.155.7 e 3.169.9, levando em conta a diferença de notação de Handbook of Mathematical Functions. (Compare A&S 17.3.11 com G&R 8.113.) Este artigo segue a notação da A&S.
- ↑ Handbook of Mathematical Functions, 17.3.11 et seq.







