Celoštevilski graf
Celoštevilski graf (tudi integralni graf) je v teoriji grafov graf katerega spekter je v celoti sestavljen iz celih števil. Ali drugače – graf je celoštevilski, če in samo če so vse njegove lastne vrednosti karakterističnega polinoma cela števila.
Pojem celoštevilskega grafa sta uvedla leta 1974 Harary in Schwenk.[1]
Zgledi
- polni graf Kn je celoštevilski za vse n. Na primer tetraedrski graf K4.
- prazni graf je celoštevilski za vse n.
- med kubičnimi simetričnimi grafi so graf napeljav, Petersenov graf, Desarguesov graf in Naurujski graf celoštevilski.
- Higman-Simsov graf, Hall-Jankov graf, Clebschev graf, Hoffman-Singletonov graf, Hoffmanov graf in Šrikhandov graf so celoštevilski.
-
Polni graf K4 (tetraedrski graf)
-
Graf napeljav (Thomsenov graf K3,3)
-
Hoffmanov graf
-
Šrikhandov graf
-
Clebschev graf
-
Desarguesov graf
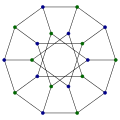
-
Naurujski graf
-
Higman-Simsov graf
-
Hall-Jankov graf
Sklici
Viri
- Harary, Frank; Schwenk, Allen J. (1974), »Which Graphs have Integral Spectra?«, v Bari, Ruth A.; Harary, Frank (ur.), Graphs and Combinatorics, Berlin: Springer-Verlag, str. 45–51, doi:10.1007/BFb0066434, ISBN 978-3-540-06854-9
Zunanje povezave
- Weisstein, Eric Wolfgang. »Integral Graph«. MathWorld.