Curiejeva temperatura
| snov |
temperatura [K] |
|---|---|
| kobalt (Co) | 1400 |
| železo (Fe) | 1043 |
| Fe2B | 1015 |
| SmCo5 | 993–1073 |
| alnico | 973–1133 |
| hematit (α-Fe2O3) | 956 |
| železov(III) oksid (Fe2O3) | 948 |
| železov(II,III) oksid (FeOFe2O3) | 858 |
| NiOFe2O3 | 858 |
| CuOFe2O3 | 728 |
| stroncijev ferit | 723 |
| MgOFe2O3 | 713 |
| MnBi | 630 |
| Cu2MnAl | 630 |
| nikelj (Ni) | 627 |
| MnSb | 587 |
| Nd2Fe14B | 583-673 |
| MnB | 578 |
| MnOFe2O3 | 573 |
| Y3Fe5O12 | 560 |
| Cu2MnIn | 500 |
| CrO2 | 386 |
| MnAs | 318 |
| gadolinij (Gd) | 292 |
| Au2MnAl | 200 |
| disprozij (Dy) | 88 |
| EuO | 69 |
| CrBr3 | 37 |
| EuS | 16,5 |
| GdCl3 | 2,2 |

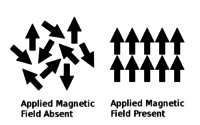
Curiejeva temperatura (TC) ali Curiejeva točka je fizikalni pojem, ki se nanaša na značilnost feromagnetne ali piezoelektrične snovi. Imenuje se po Pierru Curieju (1859–1906), ki ga je odkril leta 1895, in predstavlja temperaturo, nad katero magnetni momenti posameznih delcev niso več vzporedni.[4][5] Snov tako postane paramagnetna.
Magnetno silo določa magnetni moment, dipolni moment znotraj atoma, ki izvira od vrtilne količine in spina elektronov. Različne snovi imajo različne strukture notranjih magnetnih momentov, ki so odvisni od temperature. Curiejeva temperatura je kritična točka pri kateri notranji moment snovi spremeni smer.
Trajni magnetizem povzroča poravnava magnetnih momentov, inducirani magnetizem pa nastane, ko so neurejeni magnetni momenti prisiljeni poravnati se v zunanjem magnetnem polju. Urejeni magnetni momenti (feromagnetni) se spremenijo in postanejo neurejeni (paramagnetni) pri Curiejevi temperaturi. Z naraščanjem temperature postanejo magneti šibkejši, ker se spontana magnetizacija pojavi le pod Curiejevo temperaturo. Magnetna susceptibilnost se pojavi le nad Curiejevo temperaturo in se lahko izračuna iz Curie-Weissovega zakona, ki je izpeljan iz Curiejevega zakona.
Po podobnosti za feromagnetne in paramagnetne snovi se lahko Curiejeva temperatura rabi tudi za opis faznega prehoda med feroelektričnostjo in paraelektričnostjo. V tem kontekstu je parameter reda električna polarizacija, katere vrednost pada proti nič, ko temperatura naraste nad Curiejevo temperaturo.
Magnetini momenti
Magnetni momenti so trajni dipolni momenti znotraj atoma, ki izvirajo od vrtilne količine in spina elektronov.[6]
Elektroni znotraj atoma prispevajo magnetne momente od lastne vrtilne količine in tirne vrtilne količine okrog jedra. Magnetni momenti iz jedra so v primerjavi z magnetnimi momenti elektronov zanemarljivi.[7] Toplotna porazdelitev bo dala elektrone z višjo energijo, kar bo povzročilo nered in razpad poravnanost med dipoli.
Feromagnetne, paramagnetne, ferimagnetne in antiferomagnetne snovi imajo različne strukture notranjih magnetnih momentov. Vsaka snov ima določeno Curiejevo temperaturo kjer se ji spremenijo značilnosti. Prehod med antiferomagnetno in paramagnetno snovjo (ali obratno) se pojavi pri Néelovi temperaturi, ki je podobna Curiejevi.
| pod TC | nad TC |
|---|---|
| feromagnetno | ↔ paramagnetno |
| ferimagnetno | ↔ paramagnetno |
| antiferomagnetno | ↔ paramagnetno |
- Usmerjenosti magnetnih momentov v snoveh
-
Feromagnetizem Magnetni momenti v feromagnetni snovi. Momenti so v odsotnosti zunanjega magnetnega polja urejeni in imajo enako velikost.
-
Paramagnetizem Magnetni momenti v paramagnatni snovi. Momenti so v odsotnosti zunanjega magnetnega polja neurejeni in v prisotnosti polja urejeni.
-
Ferimagnetizem Magnetni momenti v ferimagnetni snovi. Momenti so v odsotnosti zunanjega magnetnega polja usmerjeni nasprotno in imajo različno velikost, ker so sestavljeni iz dveh različnih ionov.
-
Antiferomagnetizem Magnetni momenti v antiferomagnetni snovi. Momenti so v odsotnosti zunanjega magnetnega polja usmerjeni nasprotno in imajo enako velikost.
Snovi z magnetnimi momenti, ki spremenijo značilnosti pri Curiejevi temperaturi
Feromagnetne, paramagnetne, ferimagnetne in antiferomagnetne strukture so sestavljene iz notranjih magnetnih momentov. Če so vsi elektroni znotraj strukture v parih, se ti momenti zaradi nasprotnih spinov in vrtilne količine poničijo. Tako bodo tudi v zunanjem magnetnem polju imele različne značilnosti in Curiejeve temperature ne bo.[8][9]
Paramagnetiki
Snov je paramagnetna le nad svojo Curiejevo temperaturo. Paramagnetne snovi so nemagnetne, če ni magnetnega polja, in magnetne, če se magnetno polje uporabi. Ko magnetnega polja ni, ima snov neurejene magnetne momente, kar pomeni, da so atomi nesimetrični in neporavnani. Ko se magnetno polje uporabi, se magnetni momenti začasno na novo poravnajo vzporedno s smerjo zunanjega polja;[10][11] atomi pa so simetrični in poravnani.[12] Magnetni moment v isti smeri povzroči inducirano magnetno polje.[12][13]
Za paramagnetike je ta reakcija na zunanje magnetno polje pozitivna in je znana kot magnetna susceptibilnost.[8] Magnetna susceptibilnost velja nad Curiejevo temperaturo za neurejena stanja.[14]
Med paramagnetike (ki imajo Curiejevo temperaturo) spadajo:[15]
- vsi atomi s prostimi nesparjenimi elektroni,
- atomi katerih notranje lupine niso zapolnjene z elektroni,
- prosti radikali,
- kovine.
Nad Curiejevo temperaturo so atomi vzbujeni, usmerjenost spina postane naključna,[9] lahko pa so ponovno poravna glede na zunanje polje in snovno paramagnetnost. Pod Curiejevo temperaturo je notranja struktura izpostavljena faznemu prehodu,[16] atomi so poravnani, snov pa je feromagnetna.[12] Magnetna polja, ki jih inducirajo paramagnetne snovi, so precej šibkejša v primerjavi z magnetnimi polji feromagnetnih snovi.[16]
Feromagnetiki
Snovi so feromagnetne le pod njihovimi odgovarjajočimi Curiejevimi temperaturami. Feromagnetne snovi so magnetne, če ni zunanjega magnetnega polja.
Če ni zunanjega magnetnega polja, ima snov spontano magnetizacijo, ki je posledica urejenih magnetnih momentov, kar za feromagnetike pomeni, da so atomi simetrični in poravnani v enaki smeri, in povzročajo stalno magnetno polje.
Magnetne interakcije povezujejo skupaj izmenjalne interakcije, drugače bi toplotni nered presegel šibke interakcije magnetnih momentov. Izmenjalna interakcija ima ničelno verjetnost, da bi vzporedni elektroni zasedli enako točko v času, kar pomeni prednostno vzporedno poravnanost v snovi.[17] Boltzmannov faktor pri tem prispeva v veliki meri, saj so zaradi tega delci v interakcijah poravnani v enaki smeri.[18] To povzroča, da imajo feromagnetiki močna magnetna polja in visoke Curiejeve temperature približno 1000 K.[19]
Pod Curiejevo temperaturo so atomi poravnani in vzporedni, kar povzroča spontano magnetizacijo – snov je feromagnetna. Nad Curiejevo temperaturo je snov paramagnetna, saj atomi izgubijo svoje urejene magnetne momente, ko je snov izpostavljena faznemu prehodu.[16]
Ferimagnetiki
Snovi so le ferimagnetne pod njihovo odgovarjajočo Curiejevo temperaturo. Ferimagnetne snovi so magnetne, če ni zunanjega magnetnega polja in jih sestavljata dva različna iona.[20]
Če ni zunanjega magnetnega polja, ima snov spontano magnetizacijo, ki je posledica urejenih magnetnih momentov, kar pomeni, da so za ferimagnetike magnetni momenti enega iona poravnani v smeri z določeno velikostjo, magnetni momenti drugega iona pa so poravnani v nasprotni smeri z različno velikostjo. Ker imajo magnetni momenti različne velikosti v nasprotnih smereh, še vedno obstaja spontana magnetizacija in magnetno polje je prisotno.[20]
Podobno kot za feromagnetne snovi magnetne interakcije povezujejo skupaj izmenjalne interakcije. Vendar so usmerjenosti momentov protivzporedne, kar povzroča mrežni moment z odštevanjem njihovega momenta med seboj.[20]
Pod Curiejevo temperaturo so atomi vsakega iona poravnani protivzporedno z različnimi momenti, kar povzroča spontano magnetizacijo – snov je ferimagnetna. Nad Curiejevo temperaturo je snov paramagnetna saj atomi izgubijo svoje urejene magnetne momente, ko je snov izpostavljena faznemu prehodu.[20]
Antiferomagnetiki in Néelova temperatura
Snovi so antiferomagnetne le pod njihovo odgovarjajočo Néelovo temperaturo. To je podobno Curiejevi temperaturi saj je nad Néelovo temperaturo snov izpostavljena faznemu prehodu in postane paramagnetna.
Snov ima enake magnetne momente poravnane v nasprotnih smereh, kar povzroči ničelni magnetni moment in ničelni mrežni magnetizem pri vseh temperaturah pod Néelovo temperaturo. Antiferomagnetne snovi so šibko magnetne, če ni zunanjega uporabljenega magnetnega polja.
Podobno kot za feromagnetne snovi magnetne interakcije povezujejo skupaj izmenjalne interakcije, ki preprečujejo toplotni nered s preseganjem šibkih interakcij magnetnih momentov.[17][21] Nered se pojavi pri Néelovi temperaturi.[21]
Curie-Weissov zakon
Curie-Weissov zakon je prilagojena različica Curiejevega zakona.
Curie-Weissov zakon je preprost model, izpeljan iz aproksimacije srednjega polja, kar pomeni, da dobro deluje za temperaturo snovi T, ki je dosti večja od odgovarjajoče Curiejeve temperature TC, oziroma T >> TC; ne more pa pojasniti magnetne susceptibilnosti χ v neposredni bližini Curiejeve točke zaradi krajevnih fluktuacij med atomi.[22]
Curiejev zakon in Curie-Weissov zakon ne veljata za T < TC.
Curiejev zakon za paramagnetne snovi je:[23]
kjer je:
- – magnetna susceptibilnost, vpliv zunanjega magnetnega polja na snov,
- – magnetni momenti na enoto prostornine,
- – makroskopsko magnetno polje,
- – gostota magnetnega polja,
- – za snov značilna Curiejeva konstanta,
- [24] kjer je:
- – indukcijska konstanta. Opomba - v enotah CGS je enaka 1,[25]
- – Landéjev množitelj g,
- – lastna vrednost lastnega stanja J2 za stacionarna stanja znotraj nepopolnih atomskih lupin (nesparjeni elektroni),
- – Bohrov magneton,
- – Boltzmannova konstanta
- skupni magnetizem je N krat magnetnih momentov na enoto prostornine,
Curie-Weissov zakon se potem izpelje iz Curiejevega zakona:
kjer je:
Za polno izpeljavo glej Curie-Weissov zakon.
Fizika
Približevanje Curiejevi temperaturi od zgoraj
Ker je Curie-Weissov zakon približek, je potreben točnejši model kadar se temperatura T približuje snovni Curiejevi temperaturi TC.
Magnetna susceptibilnost se pojavi nad Curiejevo temperaturo.
Točen model kritičnega obnašanja za magnetno susceptibilnost s kritičnim eksponentom γ je:
Kritični eksponent se za snovi razlikuje in ima v modelu srednjega polja vrednost γ = 1.[27]
Ker je temperatura obratno sorazmerna magnetni susceptibilnosti, ko se T približuje TC, se imenovalec približuje 0, magnetna susceptibilnost pa narašča v neskončnost, tako da se magnetizem lahko pojavi. To je spontana magnetizacija, ki je značilnost feromagnetnih in ferimagnetnih snovi.[28][29]
Približevanje Curiejevi temperauri od spodaj
Magnetizem je odvisen od temperature in spontana magnetizacija se pojavi pod Curiejevo temperaturo. Točni model kritičnega obnašanja za spontano magnetizacijo s kritičnim eksponentom β je:
Kritični eksponent je za snovi različen in ima v modelu srednjega polja vrednost β = 0,5 kjer je T << TC.[27]
Spontana magnetizacija se približuje 0, ko se temperatura približuje snovni Curiejevi temperaturi.
Približevanje absolutni ničli (0 K)
Spontana magnetizacija, ki se pojavlja v feromagnetnih, ferimagnetnih in antiferomagnetnih snoveh, se približuje 0, ko se temperatura približuje snovni Curiejevi temperaturi. Njen maksimum je, ko se temperatura približuje absolutni ničli 0 K.[30] To pomeni, da so magnetni momenti popolnoma poravnani in imajo največjo vrednost, ker ni toplotnega vpliva.
V paramagnetnih snoveh je temperatura dovolj, da preseže urejene poravnanosti. Ko se temperatura približuje 0 K, se entropija zmanjšuje proti 0, oziroma nered se zmanjšuje, urejenost pa povečuje. To se pojavi brez prisotnosti zunanjega uporabljenega magnetnega polja in velja tretji zakon termodinjamike.[17]
Curiejev zakon in Curie-Weissov zakon ne veljata, ko se temperatura približuje 0 K. To je zaradi tega, ker sta odvisna od magnetne susceptibilnosti, ki velja le kadar je stanje neurejeno.[31]
Za gadolinijev sulfat pri 1 K še vedno velja Curiejev zakon. Med 0 in 1 K zakon ne velja več, pri Curiejevi temperaturi pa se pojavi nenadna sprememba v notranji strukturi.[32]
Isingov model faznih prehodov
Isingov model matematično temelji in lahko analizira kritične točke faznih prehodov v feromagnetiku zaradi spinov elektronov, ki imajo velikosti +/- ½. Spini interagirajo s sosednjimi dipolnimi elektroni v strukturi in tukaj lahko Isingov model predvidi njihovo medsebojno obnašanje.[33][34]
Ta model je pomemben za reševanje in razumevanje konceptov faznih prehodov in zato določevanje Curiejeve temperature. Kot rezultat se lahko analizira več različnih odvisnosti, ki vplivajo na Curiejevo temperaturo.
Površinske in prostoirninske značilnosti so na primer odvisne od poravnave in velikosti spinov in Isingov model lahko določi vplive magnetizma v takšnem sistemu.
Weissove domene, ploskovne in prostorninske Curiejeve temperature
Strukturo snovi sestavljajo notranji magnetni momenti, ki so ločeni v domene imenovane Weissove domene.[35] To lahko vodi, da so feromagnetne snovi brez spontane magnetizacije, ker se lahko domene med seboj izničijo.[35] Lega delcev ima lahko različne usmerjenosti po površini od tiste v notranjosti snovi. Ta značilnost neposredno vpliva na Curiejevo temperaturo, saj za snov obstajata prostorninska Curiejeva temperatura TB in različna površinska Curiejeva temperatura TS.[36]
Zato se lahko zgodi, da je površinska Curiejeva temperatura feromagnetna nad prostorninsko Curiejevo temperaturo, ko je glavno stanje neurejeno, oziroma, da se urejena in neurejena stanja lahko pojavijo sočasno.[33]
Površinske in prostorninske značilnosti lahko predvidi Isingov model. Za zaznavo elektronskih spinov in magnetnih momentov na površini snovi se lahko uporabi spektroskopija z zajetjem elektronov. Povprečni skupni magnetizem se vzame iz prostorninskih in površinskih temperatur za izračun Curiejeve temperature snovi, pri čemer prostorninske prispevajo več.[33][37]
Vrtilna količina elektrona je +ħ/2 ali - ħ/2, ker je njegov spin enak ½. Zaradi tega ima elektron določeno velikost magnetnega momenta, Bohrov magneton.[38] Elektroni krožeči okrog jedra v trenutni zanki tvorijo magnetno polje, ki je odvisno od Bohrovega magnetona in magnetnega kvantnega števila.[38] Zaradi tega so magnetni momenti povezani med lastno in tirno vrtilno količino in vplivajo drug na drugega. Lastna vrtilna količina prispeva k magnetnim momentom dvakrat več kot tirna.[39]
Za terbij, ki je redka kovina in ima visoko tirno vrtilno količino, je magnetni moment dovolj močan, da vpliva na stopnjo nad njegovimi prostorninskimi temperaturami. V tem smislu ima veliko anizotropijo na površini, ki je zelo usmerjena v eno smer. Na svoji površini ostaja feromegneten nad svojo Curiejevo temperaturo, njegova notranjost pa postane ferimagnetna in nato pri višjih temperaturah njegova površina ostaja ferimagnetna nad njegovo Néelovo temperaturo dokler ne postane popolnoma neurejena in paramagnetna z naraščajočo temperaturo. Anizotropija v notranjosti je različna od njegove površinske anizotropije takoj nad temi faznimi prehodi, ker bodo magnetni momenti urejeni različno ali urejeni v paramagnetnih snoveh.[36]
Spreminjanje Curiejeve temperature snovi
Kompoziti
Kompoziti, snovi sestavljene iz drugih snovi z različnimi značilnosti, lahko spremenijo Curiejevo temperaturo. Kompozit, ki vsebuje na primer srebro, lahko tvori prazna mesta za kisikove molekule v vezeh, kar zniža Curiejevo temperaturo,[40] saj kristalna mreža ne bo več tako strnjena.
Usmerjenost magnetnih momentov v kompozitu vpliva na Curiejevo temperaturo. Če so momenti snovi vzporedni med seboj, se bo zviševala, če pa so pravokotni med seboj, se bo zmanjševala,[40] saj bo potrebno več ali manj toplotne energije za uničenje poravnanosti.
Priprava kompozitov z različnimi temperaturami lahko vodi do različnih končnih sestav z različnimi Curiejevimi temperaturami.[41] Tudi dopiranje snovi lahko vpliva na njeno Curiejevo temperaturo.[41]
Gostota nanokompozitov spreminja Curiejevo temperaturo. Nanokompoziti so strnjene strukture v nanomerilu. Struktura je sestavljena z visokimi in nizkimi prostorninskimi Curiejevimi temperaturami, vendar bo imela le eno Curiejevo temperaturo srednjega polja. Večja gostota nižjih prostorninskih temperatur da nižjo Curiejevo temperaturo srednjega polja, večja gostota višje prostorninske temperature pa izdatno poveča Curiejevo temperaturo srednjega polja. V več kot eni razsežnosti se Curiejeva temperatura začne večati, saj bodo magnetni momenti potrebovali več toplotne energije za premostitev urejene strukture.[37]
Velikost delcev
Velikost delcev v kristalni mreži snovi spreminja Curiejevo temperaturo. Zaradi majhne velikosti delcev (nanodelcev) postanejo fluktuacije elektronskih spinov izrazitejše, kar povzroči, da se Curiejeva temperatura drastično zmanjša, ko se velikost delcev povečuje, saj fluktuacije povzročajo neurejenost. Velikost delcev vpliva tudi na anizotropijo, kjer poravnanost postaja manj stabilna, kar vodi do neurejenosti magnetnih momentov.[33][42]
Ekstremni primer tega je superparamagnetizem, ki se pojavlja le v majhnih feromamagnetnih delcih in tam kjer imajo fluktuacije velik vpliv, da se usmerjenost magnetnih momentov spreminja naključno in tako ustvarjajo neurejenost.
Na Curiejevo temperaturo nanodelcev vpliva tudi struktura kristalne mreže – telesno centrirana, ploskovno centrirana in heksagonalna struktura imajo vse različne Curiejeve temperature ker magnetni momenti reagirajo na svoje sosednje elektronske spine. Ploskovno centrirane in heksagonalne imajo tesnejše strukture in zaradi tega višje Curiejeve temperature od telesno centriranih saj imajo magnetni momenti močneje vplivajo, če so bližje skupaj.[33] To podaja koordinacijsko število, ki je število najbližjih sosednjih delcev v strukturi. To nakazuje nižje koordinacijsko število na površini snovi kot v notranjosti, kar vodi do tega, da površina postaja vse manj pomembna, ko se temperatura bliža Curiejevi temperaturi. V majhnih sistemih je koordinacijsko število za površino bolj pomembno in magnetni momenti močneje vplivajo na sistem.[33]
Čeprav so razlike velikosti delcev majhne, so lahko močno odvisne o strukture kristalnih mrež, ko delci reagirajo s svojimi najbližjimi sosednjimi delci. Na velikost vpliva tudi izmenjalna interakcija,[42] ker imajo prednost vzporedno usmerjeni magnetni momenti in imajo zaradi tega manj motenj in neurejenosti, zato tesnejša struktura poraja močnejši magnetizem in zato višjo Curiejevo temperaturo.
Tlak
Tlak spreminja Curiejevo temperaturo snovi. Povečani tlak v kristalni mreži zmanjšuje prostornino sistema. Tlak neposredno vpliva na kinetično energijo v delcih, ker gibanje povečuje vpliv nihanj, da se urejenost magnetnih momentov izničuje. To je podobno temperaturi, saj tudi povečuje kinetično energijo delcev in uničuje urejenost magnetnih momentov in magnetizma.[43]
Tlak vpliva tudi na gostoto stanj.[43] Tukaj se gostota stanj zmanjšuje in povzroča, da se zmanjšuje šteilo elektronov, ki so sistemu na voljo. Zaradi tega bi se pričakovalo, da se bo Curiejeva temperatura zniževala, vendar se povečuje. To je posledica izmenjalne interakcije. Izmenjalna interakcija daje prednost vzporedno poravnanim magnetnim momentom, ker elektroni istočasno ne morejo zavzemati istega prostora.[17] Ker se to zvišuje zaradi zmanjšanja prostornine, se Curiejeva temperatura s tlakom povečuje. Curiejeva temperatura je sestavljena iz kombinacije odvisnosti od kinetične energije in gostote stanj.[43]
Velja omeniti, da koncentracija delcev tudi vpliva na Curiejevo temperaturo pri uporabljenem tlaku in lahko povzroča znižanje Curiejeve temperature, ko je koncentracija nad določenim procentom.[43]
Urejenost orbital
Urejenost orbital spreminja Curiejevo temperaturo snovi. Nadzira se jo lahko prek zunanjih obremenitev.[44] To je funkcija, ki določa valovanje posameznega elektrona ali sprajenih elektronov znotraj snovi. Nadzor verjetnosti lege elektrona omogoča spreminjanje Curiejeve temperature. Delokalizirani elektroni se lahko na primer premaknejo v isto ravnino z zunanjimi obremenenitvami znotraj kristalne mreže.[44]
Curiejeva temperatura se zelo zvišuje zaradi strnjenih elektronov v isti ravnini, kjer so se prisiljeni poravnati zaradi izmenjalne interakcije in tako povečujejo jakost magnetnih momentov kar preprečuje toplotno neurejenost pri nižjih temperaturah.
Curiejeva temperatura v feroelektričnih in piezoelektričnih snoveh
Po analogiji s feromagnetnimi in paramagnetnimi snovmi se lahko s Curiejevo temperaturo opiše temperaturo pri kateri se spontana električna polarizacija spremeni v inducirano ali obratno.[45]
Električna polarizacija je posledica poravnanih ekeltričnih dipolov. Poravnani električni dipoli so sestava pozitivnih in negativnih električnih nabojev, kjer so vsi dipoli usmerjeni v eno smer. Naboji so ločeni od njihove stabilne lege v delcih in se lahko pojavijo spontano zaradi tlaka ali zunanjega električnega polja.[46]
Feroelektriki, dielektriki (paraelektriki) in piezoelektriki imajo električno polarizacijo. V feroelektrikih obstaja spontana električna polarizacija, če ni zunanjega električnega polja.[45] V dielektrikih je električna polarizacija poravnana le pri zunanjem električnem polju.[46] Piezoelektriki imajo električno polarizacijo zaradi zunanje mehanske napetosti, ki deformira strukturo zaradi tlaka.[47]
T0 je temperatura kjer feroelektriki izgubijo svojo spontano polarizacijo, ko se pojavi fazni prehod prvega ali drugega reda, oziroma, ko se spremeni notranja struktura ali notranja simetrija.[45] V določenih primerih je T0 enaka Curiejevi temperaturi, Curiejeva temperatura pa je lahko tudi nižja za 10 K od T0.[48]

| Pod T0 | Nad T0[49] |
|---|---|
| feroelektrik | ↔ dielektrik (paraelektrik) |
Vsi feroelektriki so piroelektriki[50] in piezoelektriki,[51] obratno pa ne velja.
Piezoelektriki
Zunanja sila na delce znotraj snovi povzroča tlak, ki vpliva na strukturo kristalne mreže. Delci v enotski celici postanejo nesimetrično porazdeljeni kar omogoča mrežno polarizacijo od posameznega delca. Simetrija bi izničila nasprotne naboje in ne bi bilo mrežne polarizacije.[52] Pod temperaturo prehoda T0 premik električnih nabojev povzroča polarizacijo. Nad temperaturo prehoda T0 je struktura kubična in simetrična, kar povzroča, da snov postane dielektrična. Električni naboji so tudi vzbujeni in neusmerjeni, kar povzroča, da snov nima električne polarizacije brez zunanjega električnega polja.
Feroelektriki in dielektriki
Snovi so le feroelektrične pod njihovimi odgovarjajočimi temperaturami prehoda T0.[45] Feroelektriki so vsi piezoeletriki in imajo zato spontano električno polarizacijo ker so strukture nesimetrične.
Snovi so le dielektrične pod njihovimi odgovarjajočimi temperaturami prehoda T0.[53] Dielektriki nimajo električne polarizacije brez zunanjega električnega polja. Električni dipoli so neporavnani in nimajo mrežne polarizacije. Po analogiji z magnetno susceptibilnostjo se električna susceptibilnost pojavi le nad T0.
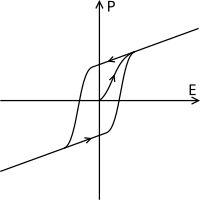
Na feroelektrike pri polarizaciji vpliva histereza. So neodvisni od svojega predhodnega stanja in tudi od sedanjega stanja. Ob zunanjem električnem polju so dipoli prisiljeni poravnati se in nastane polarizacija. Če se zunanje električno polje odstrani, polarizacija ostane. Histerezna zanka je odvisna od temperature. Ko se temperatura poveča in doseže T0 tako obe krivulji postaneta ena kakor je prikazano v dielektrični polarizaciji na sliki.[54]
Relativna dielektričnost
Modificirana različica Curie-Weissovega zakona velja za dielektrično konstanto, znano tudi kot relativna permisivnost:[48]
Pomen in uporaba
Toplotno inducirani feromagnetno-paramagnetni prehod se uporablja pri magnetooptičnih pomnilniških medijih za brisanje in zapisovanje novih podatkov. Sem spadata na primer Sonyjev format MiniDisc in sedaj zastarel format CD-MO. Uporablja se tudi v nadzoru toplote pri spajkalnikih[55] in stabilizaciji magnetnega polja tahometrskih generatorjev zaradi temperaturne spremembe.[56]
Glej tudi
- feromagnetizem
- feroelektrik
- Curiejev zakon
- Curie-Weissov zakon
- kritični pojav
- paleomagnetizem
Sklici
- ↑ Buschow (2001), str. 5021, tabela 1.
- ↑ Jullien; Guinier (1989), str. 155.
- ↑ Kittel (1986).
- ↑ »Pierre Curie - Biography«, Nobelprize.org, From Nobel Lectures, Physics 1901-1921, Elsevier Publishing Company, Amsterdam, 1967 (v angleščini), Nobelov sklad 1903, pridobljeno 14. marca 2013
- ↑ Breuer (1993), str. XXX.
- ↑ Hall; Hook (1994), str. 200.
- ↑ Jullien; Guinier (1989), str. 136–138.
- ↑ 8,0 8,1 Lüth; Ibach (2009).
- ↑ 9,0 9,1 Levy (1968), str. 236–239.
- ↑ Dekker (1958), str. 217–220.
- ↑ Levy (1968).
- ↑ 12,0 12,1 12,2 Fan (1987), str. 164–165.
- ↑ Dekker (1958), str. 454–455.
- ↑ Mendelssohn (1977), str. 162.
- ↑ Levy (1968), str. 198–202.
- ↑ 16,0 16,1 16,2 Cusack (1958), str. 269.
- ↑ 17,0 17,1 17,2 17,3 Hall; Hook (1994), str. 220–221.
- ↑ Palmer (2007).
- ↑ Hall; Hook (1994), str. 220.
- ↑ 20,0 20,1 20,2 20,3 Jullien; Guinier (1989), str. 158–159.
- ↑ 21,0 21,1 Jullien; Guinier (1989), str. 156–157.
- ↑ Jullien; Guinier (1989), str. 153.
- ↑ Hall; Hook (1994), str. 205–206.
- ↑ 24,0 24,1 Levy (1968), str. 201–202.
- ↑ Kittel (1996), str. 444.
- ↑ Myers (1997), str. 334–345.
- ↑ 27,0 27,1 Hall; Hook (1994), str. 227–228.
- ↑ Kittel (1986), str. 424–426.
- ↑ Spaldin (2010), str. 52–54.
- ↑ Hall; Hook (1994), str. 225
- ↑ Mendelssohn (1977), str. 180–181.
- ↑ Mendelssohn (1977), str. 167.
- ↑ 33,0 33,1 33,2 33,3 33,4 33,5 Bertoldi; Bringa; Miranda (2012).
- ↑ Brout (1965), str. 6–7.
- ↑ 35,0 35,1 Jullien; Guinier (1989), str. 161.
- ↑ 36,0 36,1 Rau; Jin; Robert (1988).
- ↑ 37,0 37,1 Skomski; Sellmyer (2000).
- ↑ 38,0 38,1 Jullien; Guinier (1989), str. 138.
- ↑ Hall; Hook (1994).
- ↑ 40,0 40,1 Hwang idr. (1998).
- ↑ 41,0 41,1 Jones (2003).
- ↑ 42,0 42,1 Lopez-Dominguez idr. (2012).
- ↑ 43,0 43,1 43,2 43,3 Bose idr. (2011).
- ↑ 44,0 44,1 Sadoc idr. (2010)
- ↑ 45,0 45,1 45,2 45,3 Myers (1997), str. 404–405.
- ↑ 46,0 46,1 Jullien; Guinier (1989), str. 56–59.
- ↑ Hall; Hook (1994), str. 275.
- ↑ 48,0 48,1 Webster (1999).
- ↑ Kovetz (1990), str. 116.
- ↑ Whatmore (1991), str. 283.
- ↑ Myers (1997), str. 449.
- ↑ Pascoe (1973), str. 186–187.
- ↑ Hummel (2001), str. 189.
- ↑ Pascoe (1973), str. 190–191.
- ↑ »An example of a high-frequency AC soldering iron using Curie Point to regulate temperature« (v angleščini).
- ↑ Pallàs-Areny; Webster (2001), str. 262–263.
Viri
- Bertoldi, Dalía S.; Bringa, Eduardo M.; Miranda, E. N. (6. junij 2012), »Analytical solution of the mean field Ising model for finite systems«, Journal of Physics: Condensed Matter, 24 (22): 226004, Bibcode:2012JPCM...24v6004B, doi:10.1088/0953-8984/24/22/226004, pridobljeno 12. februarja 2013
- Bose, S. K.; Kudrnovský, J.; Drchal, V.; Turek, I. (1. november 2011), »Pressure dependence of Curie temperature and resistivity in complex Heusler alloys«, Physical Review B, 84 (17), arXiv:1010.3025, Bibcode:2011PhRvB..84q4422B, doi:10.1103/PhysRevB.84.174422
- Breuer, Hans (1993), Atlas klasične in moderne fizike, Ljubljana: DZS, COBISS 35693056, ISBN 86-341-1105-9
- Brout, Robert (1965), Phase Transitions, New York, Amsterdam: W.A.Benjamin.INC
- Buschow, Kurt Heinz Jürgen (2001), Encyclopedia of materials : science and technology, Elsevier, COBISS 5171483, ISBN 0-08-043152-6
- Cusack, Norman Edward (1958), The Electrical and Magnetic Properties of Solids, Longmans, Green
- Dekker, Adrianus J. (1958), Solid State Physics, Macmillan, ISBN 978-0-333-10623-5
- Fan, Hong Y. (1987), Elements of Solid State Physics, Wiley-Interscience, ISBN 978-0-471-85987-1
- Hall, John R.; Hook, Henry Edgar (1994), Solid state physics (2. izd.), Chichester: Wiley, COBISS 34750469, ISBN 0-471-92805-4
- Hummel, Rolf E. (2001), Electronic properties of materials (3. izd.), New York [u.a.]: Springer, COBISS 23074565, ISBN 0-387-95144-X
- Hwang, Hae Jin; Nagai, Toru; Ohji, Tatsuki; Sando, Mutsuo; Toriyama, Motohiro; Niihara, Koichi (1. januar 2005), »Curie Temperature Anomaly in Lead Zirconate Titanate/Silver Composites«, Journal of the American Ceramic Society, 81 (3): 709–712, doi:10.1111/j.1151-2916.1998.tb02394.x
- Ibach, Harald; Lüth, Hans (2009), Solid-state physics : an introduction to principles of materials science (4. posodobljena in razširjena izd.), Berlin: Springer, COBISS 33430277, ISBN 978-3-540-93803-3
- Jullien, Rémi; Guinier, André (1989), The solid state from superconductors to superalloys (broširana izd.), Oxford: Oxford Univ. Press, COBISS 84527, ISBN 0-19-855554-7
- Kittel, Charles (1986), Introduction to Solid State Physics (6. izd.), John Wiley & Sons, COBISS 33380, ISBN 0-471-87474-4
- Kittel, Charles (1996), Introduction to solid state physics (7. izd.), New York [u.a.]: Wiley, COBISS 14037799, ISBN 0-471-11181-3
- Kochmański, Martin; Paszkiewicz, Tadeusz; Wolski, Sławomir (2013), »Curie-Weiss magnet: a simple model of phase transition«, European Journal of Physics, 34: 1555–1573, arXiv:1301.2141, Bibcode:2013EJPh...34.1555K, doi:10.1088/0143-0807/34/6/1555
- Kovetz, Attay (1990), The principles of electromagnetic theory (1. izd.), Cambridge [Anglija]: Cambridge University Press, ISBN 0-521-39997-1
- Levy, Robert Aaron (1968), Principles of Solid State Physics, Academic Press, ISBN 978-0124457508
- Lopez-Dominguez, Victor; Hernàndez, Joan Manel; Tejada, Javier; Ziolo, Ronald F. (8. januar 2013), »Colossal Reduction in Curie Temperature Due to Finite-Size Effects in CoFe O Nanoparticles«, Chemistry of Materials, 25 (1): 6–11, doi:10.1021/cm301927z
- Lüth, Hans; Ibach, Harald (2009), Solid-state physics: an introduction to principles of materials science (4. izd.), Berlin: Springer, ISBN 978-3-540-93803-3
- Mendelssohn, Kurt (1977), The quest for absolute zero : the meaning of low temperature physics, z enotami SI (2. izd.), London: Taylor and Francis, ISBN 0850661196
- Myers, Harold Peter (1997), Introductory solid state physics. (2. izd.), London: Taylor & Francis, COBISS 675156, ISBN 0-7484-0660-3
- Pallàs-Areny, Ramon; Webster, John G. (2001), Sensors and Signal Conditioning (2. izd.), John Wiley & Sons, str. 262–263, COBISS 2472276, ISBN 978-0-471-33232-9
- Palmer, John (2007), Planar Ising correlations ([spletna] izd.), Boston: Birkhäuser, COBISS 32551685, ISBN 978-0-8176-4620-2
- Pascoe, Kenneth J. (1973), Properties of materials for electrical engineers., New York, N.Y.: J. Wiley and Sons, ISBN 0471669113
- Paulsen, Jason A.; Lo, Chester C. H.; Snyder, John E.; Ring, A. P.; Jones, L. L.; Jiles, David C. (september 2003), »Study of the Curie temperature of cobalt ferrite based composites for stress sensor applications«, IEEE Transactions on Magnetics, 39 (5): 3316–3318, doi:10.1109/TMAG.2003.816761
{citation}: Vzdrževanje CS1: samodejni prevod datuma (povezava) - Potočnik, Anton (2009), Enodimenzionalni magnetni sistemi (PDF), arhivirano iz prvotnega spletišča (PDF) dne 5. februarja 2016, pridobljeno 4. februarja 2016
- Rau, C.; Jin, C.; Robert, M. (1. januar 1988), »Ferromagnetic order at Tb surfaces above the bulk Curie temperature«, Journal of Applied Physics, 63 (8): 3667, Bibcode:1988JAP....63.3667R, doi:10.1063/1.340679
- Sadoc, Aymeric; Mercey, Bernard; Simon, Charles; Grebille, Dominique; Prellier, Wilfrid; Lepetit, Marie-Bernadette (1. januar 2010), »Large Increase of the Curie Temperature by Orbital Ordering Control«, Physical Review Letters, 104 (4), arXiv:0910.3393, Bibcode:2010PhRvL.104d6804S, doi:10.1103/PhysRevLett.104.046804
- Skomski, Ralph; Sellmyer, David Julian (1. januar 2000), »Curie temperature of multiphase nanostructures«, Journal of Applied Physics, 87 (9): 4756, Bibcode:2000JAP....87.4756S, doi:10.1063/1.373149
- Spaldin, Nicola Ann (2010), Magnetic materials : fundamentals and applications (2. izd.), Cambridge: Cambridge University Press, ISBN 978-0-5218-8669-7
- Webster, John G. (1999), The measurement, instrumentation, and sensors handbook ([spletna] izd.), Boca Raton, Fla.: CRC Press published in cooperation with IEEE Press, str. 6.55–6.56, COBISS 21328389, ISBN 978-0-8493-8347-2
- Whatmore, R. W. (1991), Electronic Materials: From Silicon to Organics (2. izd.), New York, NY: Springer, ISBN 978-1-4613-6703-1
Zunanje povezave
- Ferromagnetic Curie Point. Video, Walter Lewin, MIT (angleško)





















