Пространство үлчәнеше
| Пространство үлчәнеше | |
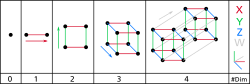 | |
| Нинди вики-проектка керә | Проект:Математика[d] |
|---|---|
| Нәрсәнең микъдары | юнәлеш[d] |

Үлчәнеш — объектның торышын сурәтләү өчен кирәк булган бәйләнешсез параметрлар саны, яки системаның азатлык дәрәҗәләре саны.
Билгеләмәләр
Үлчәнешкә билгеләмә бирүгә берничә төрле караш бар, мәсәлән
- Векторлы пространство үлчәнеше
- Күплекнең комбинаторлы үлчәнеше аның комбинаторлы үзенчәлекләре нигезендә билгеләнә һәм теләсә нинди тискәре булмаган сан булырга мөмкин[1].
- Гомумирәк билгеләмәләр үлчәнеш теориясендә бирелгән
- Лебег үлчәнеше, яки топологик үлчәнеш.
- Метрик пространствоның Хаусдорф үлчәнеше .
- Минковский үлчәнеше фракталларга гомумиләштерүне рөхсәт итә, бу вакытта аларның үлчәнеше теләсә нинди тискәре булмаган сан булырга мөмкин.
Физикада
Шулай ук карагыз: Физикада пространство
Пространство үлчәнешләре
Классик физик теорияләр өч үлчәмле физик үлчәмләрне сурәтлиләр.
Мисаллар

- Яссылыкта әйләнәнең торышын билгеләү өчен, өч параметр җитә: үзәкнең ике координатасы һәм радиусы, ягъни: яссылыкта әйләнәләр пространствосы — өч үлчәмле; шул ук йөздә нокталар пространствосы — ике үлчәмле; шулай булуга карамастан әйләнә үзе — әйләнәдәге нокталар пространствосы — бер үлчәмле: аның теләсә нинди ноктасы бер параметр белән бирелергә мөмкин.
- Безнең планета йөзенең еш кулланыла торган модельләре чикләрендә каланың торышын билгеләр өчен (кала бу очракта ике үлчәмле объект кебек каралмый, ә нокта итеп карала) Җир өстендә ике параметр бирү җитә, атап әйткәндә: географик киңлекне һәм географик озонлыкны. Ярашлы рәвештә: мондый модельләр пространствосы ике үлчәмле (кыскача — 2D, ингл. dimension) сүзеннән, карагыз. геопространство.
- Безнең физик чынбарлыкның еш кулланыла торган модельләре чикләрендә ниндидер объектның, мисал өчен — самолётның (самолёт бу очракта өч үлчәмле объект сыман каралмый, ә нокта итеп карала) торышын билгеләр өчен, өч координата күрсәтү таләп ителә — киңлек һәм озынлыкка өстәп самолёт очкан биеклекне белергә кирәк. Ярашлы рәвештә: мондый модельләр пространствосы өч үлчәмле (3D). Бу өч координатага, самолётның агымдагы торышын гына түгел, ә вакыт моментын да тасвирлау өчен, дүртенчесе өстәлергә мөмкин (вакыт). Әгәр дә модельгә самолётның ориентациясен да өстәсәң (кырынаюын, тангажны (очучы аппаратның төп (горизонталь) аркылы инерция күчәренә карата почмакча күчеше), эзләнүен (рысканье), ул чакта тагын да өч координата өстәлә һәм модельнең ярашлы абстрактлы пространствосы җиде үлчәмле булып китә.
Шулай ук карагыз
- Күп үлчәмле вакыт
- Координаталар системасы
- Өлкән үлчәнешләр
Искәрмәләр
- ↑ R. Blei Analysis in integer and fractional dimensions, — New-York: Cambridge university press, — 556 p. — 2003. — ISBN 0-511-01266-7 (netLibrary Edition), ISBN 0-521-65084-4 (hardback).