Hàm gamma

Trong toán học, hàm gamma (đại diện bằng Γ - chữ viết hoa gamma trong bảng chữ cái Hy Lạp) là một trong những phần mở rộng của các hàm số giai thừa với biến số của nó giảm xuống 1, cho các số thực và số phức. Được Daniel Bernoulli nêu ra, nếu n là một số nguyên dương,
Mặc dù các phần mở rộng khác tồn tại, định nghĩa cụ thể này là phổ biến và hữu ích nhất. Hàm gamma được xác định cho tất cả các số phức trừ các số nguyên không dương. Đối với các số phức có phần thực dương, nó được xác định thông qua tích phân suy rộng hội tụ:
Hàm tích phân này được mở rộng bằng cách tiếp tục vi phân cho tất cả các số phức trừ các số nguyên không dương (trong đó hàm có các cực đơn giản), mang lại hàm phân giác mà chúng ta gọi là hàm gamma. Nó không có số 0, vì vậy hàm gamma đối ứng 1/Γ(z) là một hàm biến hình. Trong thực tế, hàm gamma tương ứng với biến đổi Mellin của hàm số mũ âm:
Hàm gamma là một thành phần trong các hàm phân phối xác suất khác nhau và do đó nó được áp dụng trong các lĩnh vực xác suất và thống kê, cũng như tổ hợp.
Động lực
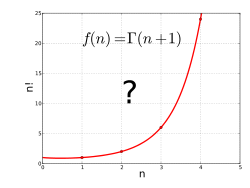
Hàm gamma có thể được xem là một giải pháp cho vấn đề nội suy sau:
- "Tìm một đường cong trơn kết nối các điểm (x, y) được cho bởi y = (x − 1)! tại các giá trị nguyên dương cho x."
Một sơ đồ của một vài giai thừa đầu tiên cho thấy một đường cong như vậy có thể được vẽ, nhưng tốt hơn là nên có một công thức mô tả chính xác đường cong, trong đó số lượng thao tác không phụ thuộc vào kích thước x. Công thức đơn giản cho giai thừa, x! = 1 × 2 × … × x, không thể được sử dụng trực tiếp cho các giá trị phân số của x vì nó chỉ hợp lệ khi x là số tự nhiên (nghĩa là số nguyên dương). Nói một cách tương đối, không có giải pháp đơn giản nào cho các giai thừa; không có sự kết hợp hữu hạn của các tổng, tích, luỹ thừa, hàm số mũ hoặc logarit sẽ đủ để thể hiện x!; nhưng có thể tìm thấy một công thức chung cho các giai thừa bằng cách sử dụng các công cụ như tích phân và giới hạn hàm từ vi tích phân. Một giải pháp tốt cho vấn đề này là hàm gamma.[1]
Có vô số phần mở rộng liên tục của giai thừa thành không nguyên: vô số đường cong có thể được vẽ thông qua bất kỳ tập hợp các điểm bị cô lập. Hàm gamma là giải pháp hữu ích nhất trong thực tế, mang tính phân tích (ngoại trừ tại các số nguyên không dương), và nó có thể được mô tả theo nhiều cách. Tuy nhiên, nó không phải là hàm phân tích duy nhất mở rộng giai thừa, vì thêm vào đó bất kỳ hàm phân tích nào bằng 0 trên các số nguyên dương, chẳng hạn như k sin mπx, sẽ cung cấp một hàm khác với thuộc tính đó.[1]

Một thuộc tính hạn chế hơn so với việc thỏa mãn phép nội suy trên là để thỏa mãn mối quan hệ lặp lại xác định phiên bản phiên dịch của hàm giai thừa,
Tham khảo
- ^ a b Davis, P. J. (1959). “Leonhard Euler's Integral: A Historical Profile of the Gamma Function”. American Mathematical Monthly. 66 (10): 849–869. doi:10.2307/2309786. JSTOR 2309786. Bản gốc lưu trữ ngày 7 tháng 11 năm 2012. Truy cập ngày 3 tháng 12 năm 2016.
Đọc thêm
- Abramowitz, Milton; Stegun, Irene A. biên tập (1972). “Chapter 6”. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover.
- Andrews, G. E.; Askey, R.; Roy, R. (1999). “Chapter 1 (Gamma and Beta functions)”. Special Functions. New York: Cambridge University Press. ISBN 978-0-521-78988-2.
- Artin, Emil (2006). “The Gamma Function”. Trong Rosen, Michael (biên tập). Exposition by Emil Artin: a selection. History of Mathematics. 30. Providence, RI: American Mathematical Society.
- Askey, R.; Roy, R. (2010), “Hàm gamma”, trong Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (biên tập), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248
- Birkhoff, George D. (1913). “Note on the gamma function”. Bull. Amer. Math. Soc. 20 (1): 1–10. doi:10.1090/s0002-9904-1913-02429-7. MR 1559418.
- Böhmer, P. E. (1939). Differenzengleichungen und bestimmte Integrale [Differential Equations and Definite Integrals]. Leipzig: Köhler Verlag.
- Davis, Philip J. (1959). “Leonhard Euler's Integral: A Historical Profile of the Gamma Function”. American Mathematical Monthly. 66 (10): 849–869. doi:10.2307/2309786. JSTOR 2309786.
- Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). “Section 6.1. Gamma Function”. Numerical Recipes: The Art of Scientific Computing (ấn bản thứ 3). New York: Cambridge University Press. ISBN 978-0-521-88068-8. Bản gốc lưu trữ ngày 27 tháng 10 năm 2021. Truy cập ngày 3 tháng 4 năm 2019.
- Rocktäschel, O. R. (1922). Methoden zur Berechnung der Gammafunktion für komplexes Argument [Methods for Calculating the Gamma Function for Complex Arguments]. Dresden: Technical University of Dresden.
- Temme, Nico M. (1996). Special Functions: An Introduction to the Classical Functions of Mathematical Physics. New York: John Wiley & Sons. ISBN 978-0-471-11313-3.
- Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis. Cambridge University Press. ISBN 978-0-521-58807-2.




