链复形

数学上，同调代数领域中的一个链复形${\displaystyle (A_{\bullet },d_{\bullet })}$是一个交换群或者模的序列A₀, A₁, A₂... 通过一系列同态d_n : A_n→A_n-1相连，使得每两个连接的映射的复合为零：d_n o d_n+1 = 0对于所有n。它们常常写作如下形式：

${\displaystyle \ldots \longrightarrow A_{n+1}{\begin{matrix}d_{n+1}\\\longrightarrow \\\,\end{matrix}A_{n}{\begin{matrix}d_{n}\\\longrightarrow \\\,\end{matrix}A_{n-1}{\begin{matrix}d_{n-1}\\\longrightarrow \\\,\end{matrix}A_{n-2}\longrightarrow \ldots \longrightarrow A_{2}{\begin{matrix}d_{2}\\\longrightarrow \\\,\end{matrix}A_{1}{\begin{matrix}d_{1}\\\longrightarrow \\\,\end{matrix}A_{0}{\begin{matrix}d_{0}\\\longrightarrow \\\,\end{matrix}0.}$

定義鏈複形的同調群為 ${\displaystyle H_{n}(A_{\bullet }):=\mathrm {Ker} (d_{n})/\mathrm {Im} (d_{n+1})}$。當所有同調群為零時，此鏈複形為正合的。

链复形概念的一个变种是上链复形。一个上链复形${\displaystyle (A^{\bullet },d^{\bullet })}$是一个交换群或者模的序列A₀, A₁, A₂...由一系列同态d_n : A_n→A_n+1相连，使得任何两个接连的映射的复合为零：d_n+1 o d_n = 0 对于所有的n:

${\displaystyle 0\longrightarrow A_{0}{\begin{matrix}d_{0}\\\longrightarrow \\\,\end{matrix}A_{1}{\begin{matrix}d_{1}\\\longrightarrow \\\,\end{matrix}A_{2}\longrightarrow \ldots \longrightarrow A_{n-1}{\begin{matrix}d_{n-1}\\\longrightarrow \\\,\end{matrix}A_{n}{\begin{matrix}d_{n}\\\longrightarrow \\\,\end{matrix}A_{n+1}\longrightarrow \ldots .}$

定義上鏈複形的上同調群為 ${\displaystyle H^{n}(A^{\bullet }):=\mathrm {Ker} (d^{n})/\mathrm {Im} (d^{n-1})}$。當所有上同調群為零時，此上鏈複形正合。想法基本上是一样的。

链复形的应用通常定义并应用它们的同调群（对于上链复形是上同调群）；在更抽象的范围里，很多等价关系被应用到复形上（例如从链同伦的思想开始，以下将解说）。链复形很容易在交换范畴中定义。

一个有界复形是其中，几乎所有的A_i为零—这样一个有限的复形，用0来伸展到左边和右边。一个例子是定义一个（有限）单纯复形的同调理论的复形。

假定我们给定一个拓扑空间X。

定义C_n(X)（对于自然数n）为自由交换群由X中的奇异单纯形形式化的生成，并定义边界映射

${\displaystyle \partial _{n}:C_{n}(X)\to C_{n-1}(X):\,(\sigma :[v_{0},\ldots ,v_{n}]\to X)\mapsto (\partial _{n}\sigma =\sum _{i=0}^{n}(-1)^{i}\sigma |[v_{0},\ldots ,{\hat {v}_{i},\ldots ,v_{n}]),}$

其中帽子表示省略一个顶点。也就是说，一个奇异单纯形的边界是限制到其面的交替和。可以证明∂² = 0，所以${\displaystyle (C_{\bullet },\partial _{\bullet })}$是一个链复形；奇异同调 ${\displaystyle H_{\bullet }(X)}$是该复形的同调类；也就是说，

${\displaystyle H_{n}(X)=\ker \partial _{n}/{\mbox{im }\partial _{n+1}$.

任何光滑流形上的微分k-形式在加法下组成一个交换群（事实上一个R-向量空间）称为Ω^k(M)。 外导数 d = d _k 映射 Ω^k(M) → Ω^k+1(M)，而且d ² = 0可以直接从二阶导数的对称性导出，所以k-形式的向量空间和外导数一起成为一个上链复形：

${\displaystyle \Omega ^{0}(M)\to \Omega ^{1}(M)\to \Omega ^{2}(M)\to \Omega ^{3}(M)\to \ldots .}$

该复形的上同调是德拉姆上同调

${\displaystyle H_{\mathrm {DR} }^{k}(M)=\ker d_{k+1}/{\mbox{im }d_{k}$.

兩個鏈複形 ${\displaystyle (A_{\bullet },d_{A,\bullet })}$、${\displaystyle (B_{\bullet },d_{B,\bullet })}$ 之間的鏈映射是一族同態 ${\displaystyle f_{n}:A_{n}\rightarrow B_{n}$，使之滿足： ${\displaystyle f_{n}\circ d_{A,n}=d_{B,n}\circ f_{n+1}$；全體鏈複形依此構成一範疇。鏈映射誘導出同調群間的映射。

上鏈複形的情形類似：兩個上鏈複形 ${\displaystyle (X^{\bullet },d_{X}^{\bullet })}$、${\displaystyle (Y^{\bullet },d_{Y}^{\bullet })}$ 之間的上鏈映射是一族同態 ${\displaystyle f^{n}:X^{n}\rightarrow Y^{n}$，使之滿足： ${\displaystyle f^{n+1}\circ d_{X}^{n}=d_{Y}^{n}\circ f^{n}$。上鏈映射也誘導出上同調群間的映射。

舉例來說，拓撲空間之間的連續映射誘導出奇異上同調的鏈映射；而光滑流形間的光滑映射則誘導出德拉姆上同調的上鏈映射。這是函子性或稱自然性的一個例子：空間與映射的拓撲/幾何性質藉此反映在代數結構上，因而變得容易操作與計算。

兩個鏈映射 ${\displaystyle f_{n},g_{n}:A_{\bullet }\rightarrow B_{\bullet }$ 稱作是同倫的，若且唯若存在一族同態 ${\displaystyle D_{n}:A_{n}\rightarrow B_{n+1}$ 使得 ${\displaystyle f_{n}-g_{n}=d_{n+1}\circ D_{n}+D_{n-1}\circ d_{n}$。

上鏈映射的同倫定義也類似，惟此時考慮的是一族同態 ${\displaystyle D^{n}:X^{n}\rightarrow Y^{n+1}$。以下給出上鏈同倫的圖解：

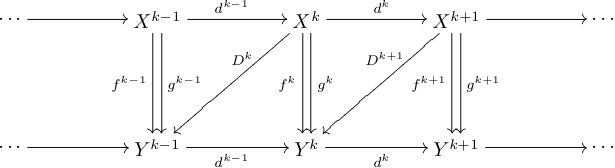
（上）鏈同倫的鏈映射在（上）同調群上誘導出相同的映射。特別是：同倫於恆等映射 id. 的（上）鏈映射是擬同構。

鏈映射的同倫可理解作單純形同倫的代數翻譯。

• 同调
• 微分分级代数