 牛顿环
牛顿环
 实验装置:一块凸透镜放在一个平面上方。
实验装置:一块凸透镜放在一个平面上方。
在光學中,牛頓環(Newton's rings),也叫做牛顿圈,是一個等厚薄膜干涉現象。將一塊平凸透鏡凸面朝下放在一塊平面透鏡上,將單色光直射向凸鏡的平面,可以觀察到一個個明暗相間的圓環條紋。若使用白光,則可以觀察到彩虹狀的圓環彩色條紋。第一個對此現象進行分析的人是英國物理學家艾薩克·牛頓爵士,因而命名為牛頓環。[1]
牛顿环现象是由平凸透镜下凸面和平面透镜的上平面(即两透镜间的空气薄膜的上下表面)所分别反射的光线产生干涉的结果。光线进入平凸透镜到达凸面进入空气时,一部分在该界面发生反射,另一部分透射后在下方的平面透镜发生反射,并与前一束后一次反射是在空气(光疏介质)—玻璃(光密介质)界面上发生的,反射光发生半波损失而与入射光反相。
牛顿环公式
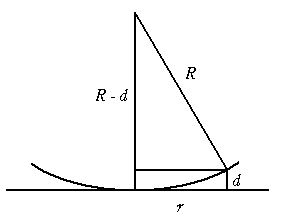
牛顿环因反射光或透射光而有所不同。公式如下:[2]
平凸透鏡和平面透鏡之間的空間薄膜的距離:

當完全相長干涉發生時:


其中m为非負整数0,1,2,……,即第一光环、第二光环……
反射光的牛顿环的强度分布公式:
透射光的牛顿环强度分布公式:
反射光牛顿环中心 ,
, ,即中心强度为零,看见黑班。
,即中心强度为零,看见黑班。
透射光牛顿环中心 ,
, ,可见亮斑。
,可见亮斑。
牛顿环的直径与透镜的半径成正比,透镜半径越大,环也越大。
牛顿环的直径与波长成正比,波长越长,环越大。即红色光的牛顿环大,蓝色光的牛顿环小。
 反射光下牛顿环随R的变化 反射光下牛顿环随R的变化
|
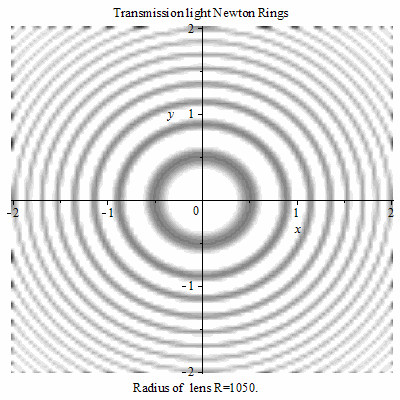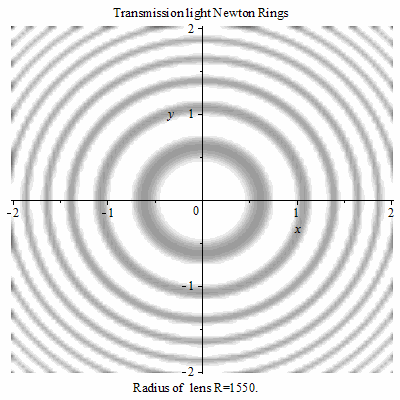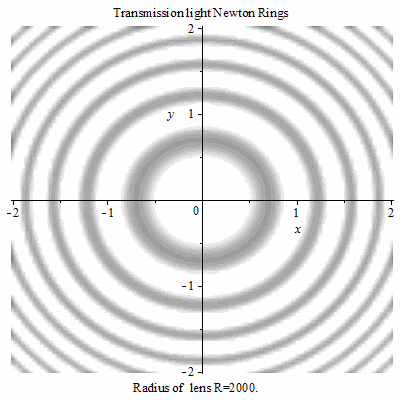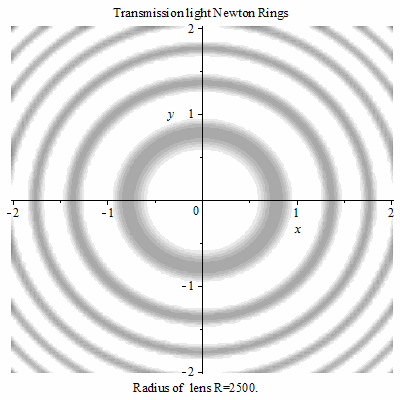 透射光牛顿环随R的变化 透射光牛顿环随R的变化
|
 反射光牛顿环随波长的变化 反射光牛顿环随波长的变化
|
 透射光牛顿环随波长的变化 透射光牛顿环随波长的变化
|
外部連結
|
|---|
| 科學著作 |
- 《流数法》(1671)
- 《物體在軌道中之運動》(1684)
- 《自然哲学的数学原理》(1687)
- 《光学》(1704)
- 《The Queries》(1704)
- 《廣義算術》(1707)
- 《用無窮級數做數學分析》(1711)
| |
|---|
| 其它著作 |
- 《若干哲學問題》(1661–1665)
- 《站在巨人的肩膀上》(1675)
- 《Notes on the Jewish Temple》(約1680)
- 《總釋》(1713;《不作假设》)
- 《古王國年表,修訂》(1728)
- 《两处著名圣经讹误的历史变迁》(1754)
|
|---|
| 貢獻 | |
|---|
| 牛頓主義 | |
|---|
| 個人 | |
|---|
| 人際關係 |
- 凱瑟琳·巴頓(侄女)
- 約翰·孔杜伊特(姪女婿)
- 艾萨克·巴罗(指導教授)
- 威廉·克拉克(指導者)
- Benjamin Pulleyn(導師)
- 约翰·基尔(徒弟)
- 威廉・斯圖凱利(好友)
- 威廉·琼斯(好友)
- 亚伯拉罕·棣莫弗(好友)
- 罗伯特·胡克(仇敵)
|
|---|
| 描繪 |
- 《牛顿》(單版畫)
- 《牛顿》(雕塑)
- 《艾薩克·牛頓雨漏》
- 《天文學家紀念碑》
|
|---|
| 相關 | |
|---|
| 分類 | |
|---|















