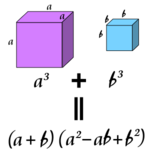
 立方和的簡單圖解
立方和的簡單圖解
立方和是數學公式的一種,它屬於因式分解、乘法公式及恆等式,被普遍使用。立方和是指一個立方數,加上另一個立方數,即是它們的總和。公式如下:[1]

立方和被因式分解後,答案分別包含二項式及三項式,與立方差相同。
驗證
主驗證
驗證此公式,可透過因式分解,首先設以下公式:

然後代入:

透過因式分解,可得:


這樣便可驗證:
和立方驗證
透過和立方可驗證立方和的原理:


那即是只要減去 及
及 便可得到立方和,可設:
便可得到立方和,可設:

- 右邊的方程

運用因式分解的方法:

![{\displaystyle =(x+y)\left[(x+y)^{2}-3xy\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bc61bdb20edf84a4973691f6064903308accd4b)


這樣便可驗證出:
幾何驗證
 圖象化
圖象化
透過繪立體的圖像,也可驗證立方和。[2]
根據右圖,設兩個立方,總和為:

把兩個立方體對角貼在一起,根據虛線,可間接得到:

要得到 ,可使用
,可使用 的空白位置。該空白位置可分割為3個部分:
的空白位置。該空白位置可分割為3個部分:



把三個部分加在一起,便得:


之後,把 減去它,便得:
減去它,便得:
 上公式發現兩個數項皆有一個公因子,把它抽出,並得:
上公式發現兩個數項皆有一個公因子,把它抽出,並得:
![{\displaystyle =(x+y)\left[(x+y)^{2}-3xy\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bc61bdb20edf84a4973691f6064903308accd4b)
 可透過和平方公式,得到:
可透過和平方公式,得到:


這樣便可證明
反驗證
透過 也可反驗證立方和。
也可反驗證立方和。




以上計算方法亦可簡化為一個表格:

| x)
|

|

|

|

|

|

|

|

|

|

|

|
這樣便可證明
立方差
立方差也可以使用立方和來驗證,例如:

把兩個數項都轉為立方數:

運用負正得負,可得:

然後運用立方和,可得:
![{\displaystyle =\left[5u+(-7v)\right]\left[25u^{2}-(5u)(-7v)+(-7v)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d2b563baed222d2b8aa5fb5c372dc7b415602d)

這個方法更可驗證到立方差的公式是
兩組立方和的數
有些整數可以有兩個立方和組合,[3]
而最少的,已是過千的1729。它是兩組不同的立方和:


下一個同樣有兩個立方和組合的整數是4104:


首十個兩組立方和的數:1729、4104、13832、20683、32832、39312、40033、46683、64232、65728
参见
參考文獻















![{\displaystyle =(x+y)\left[(x+y)^{2}-3xy\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bc61bdb20edf84a4973691f6064903308accd4b)

































![{\displaystyle =\left[5u+(-7v)\right]\left[25u^{2}-(5u)(-7v)+(-7v)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d2b563baed222d2b8aa5fb5c372dc7b415602d)














