१ − २ + ३ − ४ + · · ·

गणित में, 1 − 2 + 3 − 4 + ··· एक अनन्त श्रेणी है जिसके व्यंजक क्रमानुगत धनात्मक संख्याएं होती हैं जिसके एकान्तर चिह्न होते हैं अर्थात प्रत्येक व्यंजक के चिह्न, इसके पूर्व व्यंजक से विपरीत होते हैं। श्रेणी के प्रथम m पदों का योग सिग्मा योग निरूपण की सहायता से निम्नवत् लिखा जा सकता है:
अनन्त श्रेणी के अपसरण का मतलब यह है कि इसके आंशिक योग का अनुक्रम (1, −1, 2, −2, ...) किसी परिमित मान की ओर अग्रसर नहीं होता है। बहरहाल, 18वीं शताब्दी के मध्य में लियोनार्ड आयलर ने विरोधाभासी समीकरण में लिखा:
लेकिन इस समीकरण की सार्थकता बहुत समय बाद तक स्पष्ट नहीं हो पाई। 1980 के पूर्वार्द्ध में अर्नेस्टो सिसैरा, एमिल बोरेल तथा अन्य ने अपसारी श्रेणियों को व्यापक योग निर्दिष्ट करने के लिए सुपरिभाषित विधि प्रदान की— जिसमें नवीन आयलर विधियों का भी उल्लेख था। इनमें से विभिन्न संकलनीयता विधियों द्वारा 1 − 2 + 3 − 4 + ... का "योग" 1⁄4 लिखा जा सकता है। सिसैरा-संकलन उन विधियों में से एक है जो 1 − 2 + 3 − 4 + ... का योग प्राप्त नहीं कर सकती, अतः श्रेणी एक ऐसा उदाहरण है जिसमें थोड़ी प्रबल विधि यथा एबल संकलन विधि की आवश्यकता होती है।
श्रेणी 1 − 2 + 3 − 4 + ..., ग्रांडी श्रेणी 1 − 1 + 1 − 1 + ... से अतिसम्बद्ध है। आयलर ने इन दोनों श्रेणियों को श्रेणी 1 − 2n + 3n − 4n + ... जहाँ (n यदृच्छ है), की विशेष अवस्था के रूप में अध्ययन किया और अपने शोध कार्य को बेसल समस्या तक विस्तारित किया। बाद में उनका ये कार्य फलनिक समीकरण के रूप में परिणत हुआ जिसे अब डीरिख्ले ईटा फलन और रीमान जीटा फलन के नाम से जाना जाता है।
अपसरण
श्रेणी के पद (1, −2, 3, −4, ...) 0 की ओर अग्रसर नहीं हैं; अतः 1 − 2 + 3 − 4 + ... पद परीक्षण विधि से अपसारी प्रतीत होती है। बाद में सन्दर्भ के तौर पर यह भी आवश्यक हो गया कि श्रेणी के अपसरण का मूलभूत स्तर क्या है? परिभाषा के अनुसार किसी अनन्त श्रेणी के अपसरण या अभिसरण को उस अनुक्रम के आंशिक योग के अपसरण या अभिसरण द्वारा ज्ञात किया जाता है[1]
- 1 = 1,
- 1 − 2 = −1,
- 1 − 2 + 3 = 2,
- 1 − 2 + 3 − 4 = −2,
- 1 − 2 + 3 − 4 + 5 = 3,
- 1 − 2 + 3 − 4 + 5 − 6 = −3,
- ...
इस अनुक्रम की विशिष्टता यह है कि इसमें प्रत्येक पूर्णांक ठीक एक बार ही आता है— जिसमें शून्य भी शामिल है। यदि खाली आंशिक संकलन किया जाए— जिससे पूर्णांकों के समुच्चय की गणनीयता की स्थापना की जाती है।[2] आंशिक योग से यह स्पष्ट होता है कि श्रेणी किसी विशिष्ट संख्या पर अभिसरण नहीं करती (किसी प्रस्तावित सीमा x के लिए एक ऐसा बिन्दु प्राप्त किया जा सकता है जिसके उत्तरवर्ती सभी संकलन अन्तराल [x-1, x+1] के बाहर होंगे)। अतः 1 − 2 + 3 − 4 + ... अपसारी है।
संकलन के लिए अन्वेषण
स्थिरता एवं रैखिकता
चूँकि पद 1, −2, 3, −4, 5, −6, ... एक सरल पद्धति के अनुरूप हैं अतः श्रेणी 1 − 2 + 3 − 4 + ... स्थान परिवर्तन कर पदवार संकलित करके एक संख्यात्मक मान प्राप्त किया जा सकता है। यदि किसी साधारण संख्या s के लिए s = 1 − 2 + 3 − 4 + ... लिखना सम्भव हो तो श्रेणी का योग s = 1⁄4सिद्ध किया जा सकता है:[3]

अतः का ज्यामितीय निरुपण दायीं ओर के चित्र में दर्शाया गया है।
यद्यपि 1 − 2 + 3 − 4 + ... सामान्य अर्थों में संकलनीय नहीं है, अतः समीकरण s = 1 − 2 + 3 − 4 + ... = 1⁄4 को कथन 'यदि इस तरह का योग परिभाषित किया जाता है' के साथ समर्थित किया जा सकता है। किसी अपसारी श्रेणी के "योग" की व्यापक परिभाषा को संकलन विधि या संकलनीयता विधि कहते हैं, जो सभी सम्भव श्रेणियों के कुछ उपसमुच्चयों का योग करती है। साधारण संकलनों को प्रदर्शित करने वाली विभिन्न विधियाँ (जिनमें से कुछ का विवरण नीचे दिया गया है) हैं। उपरोक्त विवेचन से यह सिद्ध होता है कि किसी दी गई संकलनीयता विधि से जो स्थिरता एवं रैखिकता और श्रेणी 1 − 2 + 3 − 4 + ... को योग करें, तो इसका परिणामी मान 1⁄4 होगा।[4] इसके अतिरिक्त, चूँकि
ऐसी पद्धतियों से ग्रांडी श्रेणी 1 − 1 + 1 − 1 + ... = 1⁄2 का भी योग किया जा सकता है।[5]
कौशी गुणनफल
सन् १८९१ में अर्नेस्टो सिसैरा ने यह लिखते हुये- "(1 − 1 + 1 − 1 + ...)2 = 1 − 2 + 3 − 4 + ... लिखा जा सकता है और इसका मान 1⁄4 के बराबर होता है" आशा व्यक्त की कि अपसारी श्रेणियों को भी कलन के उपयुक्त माना जा सकता है।[6] सिसैरा के लिए यह समीकरण उनके पूर्व प्रकाशित पत्र की प्रमेय का एक अनुप्रयोग था जिसे अपसारी श्रेणियों के संकलन के इतिहास की प्रथम ज्ञात प्रमेय के रूप में पहचाना जा सकता है। उनकी संकलन विधि का वर्णन नीचे किया गया है; जिसकी मुख्य अवधारणा यह है कि श्रेणी 1 − 2 + 3 − 4 + ..., श्रेणी 1 − 1 + 1 − 1 + ... का श्रेणी 1 − 1 + 1 − 1 + ... के साथ कौशी गुणनफल है।
दो अनन्त श्रेणियों का कोशी गुणनफल तब भी परिभाषित है जब दोनों श्रेणियाँ अपसारी हों। इस अवस्था में, जहाँ Σan = Σbn = Σ(−1)n हो, कोशी गुणनफल के व्यंजक निश्चित विकर्ण योग द्वारा दिये जाते हैं:
इस स्थिति में गुणनफल श्रेणी निम्नवत् होगी:
अतः दो श्रेणियों का कोशी गुणनफल और योग 1 − 1 + 1 − 1 + ... = 1⁄2, का अनुसरण करने वाली संकलन विधि योग 1 − 2 + 3 − 4 + ... = 1⁄4 देगी। पूर्व अनुभाग के परिणाम के साथ वे विधियाँ जो रैखिक, स्थिरता और कोशी गुणनफल का अनुसरण करती हैं, श्रेणी 1 − 1 + 1 − 1 + ... और श्रेणी 1 − 2 + 3 − 4 + ... की संकलनीयता में समानार्थकता में अन्तर्निहित होती हैं।
सिसैरा प्रमेय एक सरल उदाहरण है। श्रेणी 1 − 1 + 1 − 1 + ... यदि दुर्बलतः सिसैरा-संकलनीय है जिसे (C, 1)-संकलनीय भी कहा जाता है, जबकि 1 − 2 + 3 − 4 + ... के लिए सिसैरा प्रमेय का प्रबलतम रूप होना अपेक्षित होता है[7] जिसे (C, 2)-संकलनीय लिखते हैं। चूँकि सिसैरा प्रमेय के सभी रूप रैखिक और स्थायी होते हैं, इसके योग की भी गणना की जा सकती है।
विशिष्ट पद्धतियाँ
सिसैरो और होल्डर

श्रेणी 1 − 2 + 3 − 4 + ... का सिसैरो संकलन (C, 1) ज्ञात करने के लिए माना श्रेणी का सिसैरा संकलन विद्यमान है अतः सर्वप्रथम श्रेणी के आंशिक योग के समान्तर माध्य की गणना करते हैं। श्रेणी का आंशिक योग:
- 1, −1, 2, −2, 3, −3, ...,
और इन योगों का समान्तर माध्य निम्नवत् दिया जाता है:
- 1, 0, 2⁄3, 0, 3⁄5, 0, 4⁄7, ....
चूँकि माध्य का अनुक्रम अभिसारी नहीं है अतः श्रेणी 1 − 2 + 3 − 4 + ... सिसैरा संकलनीय नहीं है।
सिसैरा संकलन के मुख्यतः दो व्यापकीकरण काम में लिये जाते हैं: प्राकृत संख्या n के लिए (H, n) के अनुक्रम की विधि संकल्पनात्मक रूप से इन दोनों में से सरल है। (H, 1) योग को सिसैरा संकलन कहते हैं और उच्चतर विधियाँ माध्य के अभिकलन की पुनरावृत्ति करती हैं। उपरोक्त में सभी सम पदों का माध्य 1⁄2 प्राप्त होता है जबकि विषम पदों का माध्य 0 के बराबर होता है, अतः माध्यों का माध्य 0 और 1⁄2 के औसत पर अभिसरण करता है जिसका मान 1⁄4 प्राप्त होता है।[8] अतः 1 − 2 + 3 − 4 + ..., (H, 2) संकलनीय है जिसका मान 1⁄4 प्राप्त होता है।
यहाँ "H" ऑटो होल्डर के लिए प्रतीकत्व है, जिन्होंने सर्वप्रथम 1882 में एबल संकलन और (H, n) संकलन में सम्बंध को सिद्ध किया था; 1 − 2 + 3 − 4 + ... उनका प्रथम उदाहरण था।[9] 1 − 2 + 3 − 4 + ... का (H, 2) योग 1⁄4 होना इस तथ्य की प्रत्याभूति करता है कि यह एबल योज्य है; इसकी उपपत्ति नीचे की गई है।
सिसैरा संकलन का अन्य सूत्रबद्ध व्यापकीकरण (C, n) अनुक्रम विधि है। यह सिद्ध किया जा चुका है कि (C, n) संकलन और (H, n) संकलन हमेशा समान परिणाम देते हैं लेकिन दोनों की ऐतिहासिक पृष्ठभूमि भिन्न है। सन् 1887 में, सिसैरा ने (C, n) संकलन को लगभग परिभाषित किया था लेकिन उन्होंने केवल कुछ उदाहरण ही दिये। विशेष रूप से उन्होंने 1 − 2 + 3 − 4 + ..., का योग किसी विधि से 1⁄4 प्राप्त किया जिसे (C, n) के रूप में कथित किया जा सकता है लेकिन वो उस समय पर उचित तरीके से नहीं समझा पाये। उन्होंने 1890 में औपचारिक रूप से (C, n) विधि परिभाषित की जिसके अनुसार (C, n)-संकलनीय श्रेणी और (C, m)-संकलनीय श्रेणी का कोशी गुणनफल (C, m + n + 1)-संकलनीय होता है।[10]
एबल संकलन

सन् 1749 की एक रपट के अनुसार, लियोनार्ड आयलर ने स्वीकार किया था कि श्रेणी अपसारी है लेकिन किसी न किसी प्रकार से इसका योग ज्ञात किया जा सकता है:
...जब यह कहा गया कि इस तरह की श्रेणी जैसे 1−2+3−4+5−6 आदि का योग 1⁄4 है तो यह विरोधाभासी प्रतीत होना चाहिए। इस श्रेणी के प्रथम 100 पदों को जोड़ने पर हमें −50 प्राप्त होता है तथापि 101 पदों का योग +51 प्राप्त होता है जो 1⁄4 से बिलकुल भिन्न है और आगे भी यह मान इकाई से बढ़ता है जब हम एक पद और बढ़ाते हैं। लेकिन मैंने इससे पहले भी इसे देखा था कि शब्द योग को एक विस्तृत मतलब देना बहुत ही आवश्यक है....[11]
आयलर ने शब्द "योग" को लिए विभिन्न समयों पर एक व्यापकीकृत करने का प्रस्ताव रखा; इसे अनन्त श्रेणी पर आयलर (Euler on infinite series) में देखा जा सकता है। 1 − 2 + 3 − 4 + ..., की स्थिति में उनके विचार समरूप थे जिन्हें एबल संकलन के नाम से जाना जाता है:
...यह संदेहपूर्ण नहीं है कि श्रेणी 1−2+3−4+5 + आदि का योग 1⁄4 है; चूँकि यह श्रेणी सूत्र 1⁄(1+1)2 के विस्तार से प्राप्त होती है जिसका मान निर्विवादित रूप से 1⁄4 है। यह विचार और अधिक स्पष्ट करने के लिए माना 1 − 2x + 3x2 − 4x3 + 5x4 − 6x5 + &c एक व्यापक श्रेणी है जो व्यंजक 1⁄(1+x)2 का विस्तार करने पर प्राप्त होती है, यह श्रेणी x = 1 रखने पर भी समान रहेगी।[12]
यहाँ पर यह देखने की विभिन्न विधियाँ हैं जिनमें कम से कम निरपेक्ष मानों |x| < 1, के लिए आयलर के अनुसार:
दक्षिण-हस्थ दिशा में टेलर श्रेणी विस्तार करने पर और बहुपदों के लिए वृहत भाग प्रक्रिया लागू करने पर।[13]
आधुनिक विचारों के अनुसार श्रेणी 1 − 2x + 3x2 − 4x3 + ..., x = 1 पर कोई फलन परिभाषित नहीं करती अतः परिणामी व्यंजक में वह मान सीधे ही प्रयुक्त नहीं किया जा सकता। चूँकि फलन सभी |x| < 1 के लिए परिभाषित है अतः x के 1 की ओर अग्रसर मान का सीमान्त मान प्राप्त कर सकता है और यही एबल योग की परिभाषा है:
आयलर और बोरल
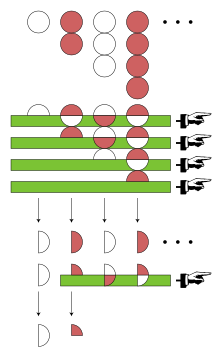
आयलर ने श्रेणी पर अन्य प्रविधि प्रयुक्त की: आयलर रचनांतर, उनके आविष्कारों में से एक। आयलर रचनांतर की गणना करने के लिए सर्वप्रथम धनात्मक पदों के अनुक्रम से आरम्भ करते हैं जो एकांतर श्रेणी का निर्माण करता है— वर्तमान अवस्था में यह श्रेणी 1, 2, 3, 4, .... है। इस श्रेणी के प्रथम अवयव को a0 से अंकित किया जाता है।
इसके बाद 1, 2, 3, 4, ... में अग्र अन्तरालों का एक अनुक्रम परिभाषित किया जाता है; जो केवल 1, 1, 1, 1, .... प्राप्त होता है। इस अनुक्रम के प्रथम पद को Δa0 से अंकित किया जाता है। आयलर रचनांतर अंतरों के अंतर और उच्च पुनरावृत्तियों पर भी निर्भर करता है लेकिन 1, 1, 1, 1, ... के सभी अग्र अंतर 0 ही प्राप्त होते हैं। अतः 1 − 2 + 3 − 4 + ... के आयलर रचनांतर को निम्नवत् परिभाषित किया जाता है:
आधुनिक पारिभाषित शब्दावली में 1 − 2 + 3 − 4 + ... आयलर संकलनीय है जिसका मान 1⁄4 प्राप्त होता है।
आयलर संकलनीयता में अन्य प्रकार की संकलनीयता भी अंतर्निहित है। 1 − 2 + 3 − 4 + ... को निम्नवत् लिखा जा सकता है:
जिससे सर्वत्र-अभिसारी श्रेणी निम्नवत् सम्बंधित है:
अतः श्रेणी 1 − 2 + 3 − 4 + ... का बोरल योग निम्न होगा:[14]
मापक पृथक्करण
सैचेव और वय्कज़िनस्की दो भौतिक सिद्धान्तों: अत्यल्प विश्रांति और मापक पृथक्करण की सहायता से परिणाम 1 − 2 + 3 − 4 + ... = 1⁄4 पर पहुंचे। इन सिद्धान्तों को यथार्थ उन्होंने एक विस्तृत "φ-संकलन विधि" का परिवार जिसमें उन सभी श्रेणियों को रखा गया जिनका योग 1⁄4 प्राप्त होता है, परिभाषित किया:
- यदि φ(x) एक फलन है जिसका प्रथम एवं द्वितीय अवकलज परास (0, ∞) में इस प्रकार सतत और समाकलनीय हैं कि φ(0) = 1 और φ(x) एवं xφ(x) का +∞ पर सीमान्त मान 0 होता है तब[15]
यह हल एबल संकलन का व्यापकीकरण है जिसे φ(x) = exp(−x) लिखकर प्राप्त किया जा सकता है। व्यापक कथन श्रेणी के m पदों को युग्मित करके व्यंजकों को रीमान-समाकल में परिवर्तित करके प्राप्त किया जा सकता है। बाद वाले पद के लिए, श्रेणी 1 − 1 + 1 − 1 + ... का हल सिद्ध करने के लिए माध्यमान प्रमेय प्रयुक्त किया जाता है लेकिन टेलर प्रमेय की भांति कठिन भाषा की आवश्यकता होती है।
व्यापकीकरण

श्रेणी 1 − 1 + 1 − 1 + ... का तिहरा कोशी गुणनफल श्रेणी 1 − 3 + 6 − 10 + ... प्राप्त होती है जो त्रिकोण संख्याओं की श्रेणी है; इसका एबल और आयलर योग 1⁄8 है।[16] श्रेणी 1 − 1 + 1 − 1 + ... का चतुर्थ कोशी गुणनफल करने पर श्रेणी 1 − 4 + 10 − 20 + ... प्राप्त होती है जो चतुष्फलकीय संख्याओं की एकान्तर श्रेणी है, इसका एबल योग 1⁄16 प्राप्त होता है।
श्रेणी 1 − 2 + 3 − 4 + ... का n के अन्य मानों के लिए श्रेणी 1 − 2n + 3n − 4n + ... में व्यापकीकरण किय जा सकता है। धनात्मक संख्याओं n के लिए श्रेणी का एबल योग निम्नवत् है:[17]
जहाँ Bn बर्नूली संख्याएँ हैं। n के सम मानों के लिए
पिछला योग नील्स हेनरिक एबल द्वारा 1826 में विशेष उपहास का विषय बताया गया:
"अपसारी श्रेणियों पूर्णतया शैतानों के कार्य पर है और यह शर्म की बात है कि इस पर कई उपपत्तियाँ पाने की हिम्मत की जाती है। जब इससे बाहर आ सकता है जिसे कोई काम में लेना चाहता है और ये वो हैं जो अप्रसन्नता सूचक है तथा इसमें बहुत ही विरोधाभास हैं। क्या यहाँ पर निम्नलिखित को लागू करने से अधिक कुछ सोचा जा सकता है
- 0 = 1 − 2n + 3n − 4n + etc.
जहाँ n एक धनात्मक संख्या है। यहाँ पर दोस्तों पर थोड़ा मुस्कराया जा सकता है।"[18]
सिसैरो के गुरु यूजीन चार्ल्स कैटलन ने भी अपसारी श्रेणियों की उपेक्षा की। कैटलन के प्रभाव से सिसैरो ने भी प्रारम्भ में श्रेणी 1 − 2n + 3n − 4n + ... के लिए "अर्थहीन समानता" के रूप में "परम्परागत सूत्रों" को उल्लिखित किया और 1883 में सिसैरो ने उस समय का प्रारूपिक दृष्टिकोण व्यक्त किया जिसके अनुसार वो सूत्र गलत थे लेकिन अभी भी औपचारिक रूप से उपयोगी हैं। अंततः 1890 में सिसैरा सुर ला मल्टीप्लिकेशन देज़ सिरीज़ (श्रेणी के गुणा पर) में परिभाषा से आरम्भ करते हुये एक आधुनिक दृष्टिकोण प्रस्तुत किया।[19]
श्रेणियों का अध्ययन n के अपूर्णांक मानों के लिए भी किया गया; इससे ही डीरिख्ले ईटा फलन का निर्माण हुआ। श्रेणी 1 − 2 + 3 − 4 + ... से सम्बंधित श्रेणियाँ अध्ययन करना आयलर की प्रेरणा का भाग ईटा फलन का फलनिक समीकरण था, जो सीधे रीमान जीटा फलन की फलनिक समीकरण देती है। आयलर ने धनात्मक सम संख्याओं (बेसल समस्या सहित) पर इन फलनों के मान प्राप्त करने के लिए प्रसिद्धि प्राप्त की और उन्होंने धनात्मक विषम संख्याओं के लिए भी समान कोशिश की, जो वर्तमान में भी एक निवारणहीन समस्या बनी हुई है। विशेष रूप से ईटा फलन आयलर विधि से काम में लेना सरल है क्योंकि इसकी डीरिख्ले श्रेणी सर्वत्र एबल संकलनीय है; जीटा फलन का डीरिख्ले श्रेणियाँ अपसारी होने पर, उनका योग बहुत कठिन है।[20] उदाहरण के लिए, जीटा फलन में श्रेणी 1 − 2 + 3 − 4 + ... का प्रतिरूप अन्-एकान्तर श्रेणी 1 + 2 + 3 + 4 + ... है, जिसके आधुनिक भौतिकी में गहरा अनुप्रयोग हैं लेकिन योग के लिए बहुत कठिन विधियों की आवश्यकता होगी।
सन्दर्भ
- ↑ हार्डी पृ॰ 8
- ↑ बील्स पृ॰ 23
- ↑ हार्डी (पृ॰6) ने ग्रांडी श्रेणी 1 − 1 + 1 − 1 + ... के परिगणन के साथ संयोजन में इसकी व्युत्पति की है।
- ↑ हार्डी पृ॰6
- ↑ हार्डी पृ॰6
- ↑ फेरारो, पृ॰130.
- ↑ हार्डी, पृ॰ 3; वाइडलिच, पृष्ठ 52–55.
- ↑ हार्डी, पृष्ठ 9, गणनाओं की पूर्ण जानकारी के लिए देखें: वाइडलिच, पृष्ठ 17–18
- ↑ फेरारो, पृष्ठ 118; टुचावान, पृष्ठ 10; फेरारो टुचावान की व्याख्या की समालोचना करते हैं (पृष्ठ 7) कि होल्डर ने किस तरह व्यापक परिणाम को सोचा, जबकि दो लेखक होल्डर के 1 − 2 + 3 − 4 + ... पर कार्य की व्याख्या करते हैं वो समान है।
- ↑ फेरारो, पृष्ठ 123–128.
- ↑ आयलर और अन्य, पृष्ठ 2; यद्यपि यह पत्र 1749 में लिखा गया था लेकिन 1768 तक प्रकाशित नहीं हो सका। [...when it is said that the sum of this series 1−2+3−4+5−6 etc. is 1⁄4, that must appear paradoxical. For by adding 100 terms of this series, we get −50, however, the sum of 101 terms gives +51, which is quite different from 1⁄4 and becomes still greater when one increases the number of terms. But I have already noticed at a previous time, that it is necessary to give to the word sum a more extended meaning....]
- ↑ आयलर और अन्य, पृष्ठ 3, 25. [...it is no more doubtful that the sum of this series 1−2+3−4+5 + etc. is 1⁄4; since it arises from the expansion of the formula 1⁄(1+1)2, whose value is incontestably 1⁄4. The idea becomes clearer by considering the general series 1 − 2x + 3x2 − 4x3 + 5x4 − 6x5 + &c. that arises while expanding the expression 1⁄(1+x)2, which this series is indeed equal to after we set x = 1.]
- ↑ कुछ उदाहरण, लेविन (पृष्ठ 23) लम्बे विभाजन की बाद करते हैं लेकिन इसको हल नहीं करते; व्रेतब्लाद (पृष्ठ 231) कोशी गुणन की गणना करते हैं। आयलर इसे अस्पष्ट लिखते हैं; देखें आयलर और अन्य, पृष्ठ 3, 26. जॉन बैज़ ने भी एक श्रेणी-सैद्धांतिक विधि सुझावित की है जिसमें सुतीक्ष्ण समुच्चयों और क्वांटम सरल आवर्ती दोलक के गुणन शामिल हैं। बैज़, जॉन सी॰ Euler's Proof That 1 + 2 + 3 + ... =-1/12 (पीडीएफ) Archived 2012-10-30 at the वेबैक मशीन math.ucr.edu (19 दिसम्बर 2003). अभिगमन तिथि: 28 मार्च 2014
- ↑ व्रेतब्लाद पृष्ठ 59
- ↑ सैकेव और वोयच्यासकी, पृष्ठ 260–264.
- ↑ क्लाइन, पृष्ठ 313.
- ↑ नॉप्प, पृष्ठ 491; यहाँ पर हार्डी (पृष्ठ 3) में एक त्रुटि प्रतीत होती है।
- ↑ ग्रत्तन-गिनीज, पृष्ठ 80; मूल फ़्रांसीसी से अन्य अनुवाद के लिए मार्कुशेविच (पृष्ठ 48) देखें; लेकिन स्वर लगभग समान रहता है।
- ↑ फेरारो, पृष्ठ 120–128.
- ↑ आयलर और अन्य, पृष्ठ 20–25.
पादटिप्पणी
- बील्स, रिचर्ड (2004). Analysis: an introduction [विश्लेषण: एक परिचय] (अंग्रेज़ी में). कैम्ब्रिज यूपी. आई॰ऍस॰बी॰ऍन॰ 0-521-60047-2.
- डेविस, हैरी एफ॰ (मई 1989). Fourier Series and Orthogonal Functions [फूरिये श्रेणी और लाम्बिक फलन] (अंग्रेज़ी में). डोवर. आई॰ऍस॰बी॰ऍन॰ 0-486-65973-9.
- आयलर, लियोनार्ड (1768). "Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques" [साधारण और व्युत्क्रम घात श्रेणियों के मध्य सुन्दर संबंध पर टिप्पणी]. Memoires de l'academie des sciences de Berlin (फ़्रेंच में). 17: 83–106. मूल से 10 जुलाई 2012 को पुरालेखित. अभिगमन तिथि 17 फ़रवरी 2014.
- फेरारो, गियोवन्नी (जून 1999). "The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics" [किसी अपसारी श्रेणी के संकलन की प्रथम आधुनिक परिभाषा: बीसवीं सदी की गणित के विकास का एक पहलू]. आर्काइव फॉर हिस्ट्री ऑफ़ एक्सॅक्ट साइंसेज (अंग्रेज़ी में). 54 (2): 101–135. डीओआइ:10.1007/s004070050036.
- ग्रत्तन-गिनीज, आइवर (1970). The development of the foundations of mathematical analysis from Euler to Riemann [आयलर से रीमान तक गणितीय विश्लेषण की नींव का विकास] (अंग्रेज़ी में). एमआईटी प्रेस. आई॰ऍस॰बी॰ऍन॰ 0-262-07034-0.
- हार्डी, जी॰एच॰ (1949). Divergent Series [अपसारी श्रेणी] (अंग्रेज़ी में). क्लेरेंडॉन प्रेस. LCCN 91075377.
- क्लाइन, मॉरिस (नवम्बर 1983). "Euler and Infinite Series" [आयलर और अनन्त श्रेणी]. मैथेमेटिक्स मैगज़ीन (अंग्रेज़ी में). 56 (5): 307–314. JSTOR 2690371. डीओआइ:10.2307/2690371.
- लेविन, शौघन (1994). Understanding the Infinite [अनन्त को समझना] (अंग्रेज़ी में). हार्वर्ड यूपी. आई॰ऍस॰बी॰ऍन॰ 0-674-92096-1.
- मार्कुशेविच, ए॰आई॰ (1967). Series: fundamental concepts with historical exposition [श्रेणियाँ: ऐतिहासिक प्रदर्शनी के साथ मूलभूत अवधारणा] (रूसी भाषा के तृतीय संस्करण (1961) का अंग्रेज़ी अनुवाद संस्करण). हिन्दुस्तान पब्लिकेशन कॉर्पोरेशन. LCCN sa68017528.
- सैकेव, ए॰आई॰ और ड्ब्ल्यू॰ए॰ वोयच्यासकी (1996). Distributions in the physical and engineering sciences, Volume 1 [भौतिक और अभियांत्रिकी विज्ञान में वितरण, भाग १] (अंग्रेज़ी में). बिरखौसर. आई॰ऍस॰बी॰ऍन॰ 0-8176-3924-1.
- टुचावान, जॉन (जनवरी 1973). "The development of the theory of summable divergent series from 1880 to 1925" [१९८० से १९२५ तक के संकलनीय अपसारी श्रेणियों के सिद्धान्त का विकास]. आर्काइव फॉर हिस्ट्री ऑफ़ एक्सॅक्ट साइंसेज. 10 (1–2): 1–40. डीओआइ:10.1007/BF00343405.
- व्रेतब्लाद, ऐन्डर्स (2003). Fourier Analysis and Its Applications [फूरिये विश्लेषण और इसके अनुप्रयोग] (अंग्रेज़ी में). स्प्रिंगर. आई॰ऍस॰बी॰ऍन॰ 0-387-00836-5.
- वाइडलिच, जॉन ई॰ (जून 1950). Summability methods for divergent series [अपसारी श्रेणियों के लिए संकलियनता विधियाँ] (अंग्रेज़ी में). स्टैनफोर्ड एम॰एस॰ थिसिस. OCLC 38624384.



![{\displaystyle {\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+(1-2)+(3-4+5-6\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}-1+(3-4+5-6\cdots )\\&=&1+&(1-2+3-4+\cdots )&{}+(-2+3-4+5+\cdots )&{}+(-2+3-4+5+\cdots )&{}+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&{}+(-2+3+3-4)&{}+(3-4-4+5)&{}+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30a6576c86da4caf35766c0f081d6841fc017445)


![{\displaystyle {\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d43c146014f7b19d308aac55a97463246ebe5c9)










