೧-೨+೩-೪…..

ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿ, 1 − 2 + 3 - 4 + · · ಒಂದು ಅನಂತ ಸರಣಿಯಾಗಿದ್ದು, ಅದರ ಅಭಿವ್ಯಕ್ತಿಗಳು ಪರ್ಯಾಯ ಚಿಹ್ನೆಗಳೊಂದಿಗೆ ಸತತ ಧನಾತ್ಮಕ ಸಂಖ್ಯೆಗಳಾಗಿವೆ, ಅಂದರೆ, ಪ್ರತಿ ಅಭಿವ್ಯಕ್ತಿಯು ವಿರುದ್ಧ ಚಿಹ್ನೆಯನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಸರಣಿಯ ಮೊದಲ ಮೀ ಪದಗಳ ಮೊತ್ತವನ್ನು ಸಿಗ್ಮಾ ಮೊತ್ತದ ಪ್ರಾತಿನಿಧ್ಯದ ಸಹಾಯದಿಂದ ಈ ಕೆಳಗಿನಂತೆ ಬರೆಯಬಹುದು: $${\displaystyle \sum _{n=1}^{m}n(-1)^{n-1}.}$$

ಅನಂತ ಸರಣಿಯ ಅಪಸರಣ ಎಂದರೆ ಅದರ ಭಾಗಶಃ ಮೊತ್ತದ (1, -1, 2, -2, ...) ಅನುಕ್ರಮವು ಯಾವುದೇ ಸೀಮಿತ ಮೌಲ್ಯವನ್ನು ಸಮೀಪಿಸುವುದಿಲ್ಲ. ಆದಾಗ್ಯೂ, 18 ನೇ ಶತಮಾನದ ಮಧ್ಯದಲ್ಲಿ ಲಿಯೊನಾರ್ಡ್ ಯೂಲರ್ ವಿರೋಧಾತ್ಮಕ ಸಮೀಕರಣದಲ್ಲಿ ಬರೆದರು: $${\displaystyle 1-2+3-4+\cdots ={\frac {1}{4}.}$$

ಆದರೆ ಬಹಳ ಸಮಯದ ನಂತರ ಈ ಸಮೀಕರಣದ ಮಹತ್ವವು ಸ್ಪಷ್ಟವಾಗಿಲ್ಲ. 1980 ರ ದಶಕದ ಆರಂಭದಲ್ಲಿ, ಅರ್ನೆಸ್ಟೊ ಸೆಸ್ರೊ, ಮೈಲ್ ಬೊರೆಲ್ ಮತ್ತು ಇತರರು ಹೊಸ ಯೂಲರ್ ವಿಧಾನಗಳನ್ನು ಒಳಗೊಂಡಂತೆ ವಿಭಿನ್ನ ಸರಣಿಗಳಿಗೆ ಸಾಮಾನ್ಯ ಮೊತ್ತವನ್ನು ನಿಯೋಜಿಸಲು ಉತ್ತಮವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ವಿಧಾನವನ್ನು ಒದಗಿಸಿದರು. 1 − 2 + 3 - 4 + ... ನ "ಮೊತ್ತ" ವನ್ನು ವಿವಿಧ ಹೊಂದಾಣಿಕೆ ವಿಧಾನಗಳಿಂದ 1⁄4 ಎಂದು ಬರೆಯಬಹುದು. ಸೆಸ್ರೊ-ಸಂಕಲನವು 1 - 2 + 3 - 4 + ... ಮೊತ್ತವನ್ನು ಪಡೆಯಲು ಸಾಧ್ಯವಾಗದ ವಿಧಾನಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ, ಆದ್ದರಿಂದ ಸರಣಿಯು ಅಬೆಲ್ ಸಂಕಲನ ವಿಧಾನದಂತಹ ಸ್ವಲ್ಪ ಬಲವಾದ ವಿಧಾನದ ಅಗತ್ಯವಿರುವ ಒಂದು ಉದಾಹರಣೆಯಾಗಿದೆ.

ಸರಣಿ 1 - 2 + 3 - 4 + ... ಗ್ರ್ಯಾಂಡಿ ಸರಣಿ 1 - 1 + 1 - 1 + ... ಗೆ ನಿಕಟ ಸಂಬಂಧ ಹೊಂದಿದೆ. ಯೂಲರ್ ಈ ಎರಡು ಸರಣಿಗಳನ್ನು 1 - 2n + 3n - 4n + ... ಸರಣಿಯ ವಿಶೇಷ ಷರತ್ತುಗಳಾಗಿ ಅಧ್ಯಯನ ಮಾಡಿದರು (n ಯಾದೃಚ್ಛಿಕ), ಮತ್ತು ಅವರ ಸಂಶೋಧನಾ ಕಾರ್ಯವನ್ನು ಬಾಸೆಲ್ ಸಮಸ್ಯೆಗೆ ವಿಸ್ತರಿಸಿದರು. ನಂತರ ಅವರ ಕೆಲಸವು ಕ್ರಿಯಾತ್ಮಕ ಸಮೀಕರಣಗಳಿಗೆ ಕಾರಣವಾಯಿತು, ಇವುಗಳನ್ನು ಈಗ ಡಿರಿಚ್ಲೆ ಎಟಾ ಫಂಕ್ಷನ್ ಮತ್ತು ರೀಮನ್ ಝೀಟಾ ಫಂಕ್ಷನ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಸರಣಿಯಲ್ಲಿನ ಪದಗಳು (1, -2, 3, -4, ...) 0 ಗೆ ಕಾರಣವಾಗುವುದಿಲ್ಲ; ಆದ್ದರಿಂದ 1 - 2 + 3 - 4 + ... ಪದವು ಪರೀಕ್ಷಾ ವಿಧಾನದಿಂದ ಭಿನ್ನವಾಗಿದೆ. ನಂತರ ಸನ್ನಿವೇಶದಲ್ಲಿ ಸರಣಿಯ ಭಿನ್ನತೆಯ ಮೂಲಭೂತ ಮಟ್ಟ ಯಾವುದು? ವ್ಯಾಖ್ಯಾನದ ಪ್ರಕಾರ, ಅನಂತ ಸರಣಿಯ ಭಿನ್ನತೆ ಅಥವಾ ಒಮ್ಮುಖವನ್ನು ಆ ಅನುಕ್ರಮದ ಆಂಶಿಕ ಮೊತ್ತದ ಡೈವರ್ಜೆನ್ಸ್ ಅಥವಾ ಒಮ್ಮುಖದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ[1]

ಈ ಅನುಕ್ರಮದ ವಿಶಿಷ್ಟತೆಯು ಶೂನ್ಯವನ್ನು ಒಳಗೊಂಡಂತೆ ಪ್ರತಿ ಪೂರ್ಣಾಂಕವು ನಿಖರವಾಗಿ ಒಮ್ಮೆ ಸಂಭವಿಸುತ್ತದೆ. ಖಾಲಿ ಭಾಗಶಃ ಸಂಕಲನವನ್ನು ಮಾಡಬೇಕಾದರೆ - ಪೂರ್ಣಾಂಕಗಳ ಸೆಟ್ Z {\displaystyle\mathbb {Z} } ನ ಎಣಿಕೆಯನ್ನು ಸ್ಥಾಪಿಸಲಾಗಿದೆ.[2] ಆಂಶಿಕ ಮೊತ್ತದಿಂದ ಸರಣಿಯು ಯಾವುದೇ ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯಲ್ಲಿ ಒಮ್ಮುಖವಾಗುವುದಿಲ್ಲ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ (ಯಾವುದೇ ಪ್ರಸ್ತಾವಿತ ಮಿತಿ x ಗೆ ಅಂತಹ ಬಿಂದುವನ್ನು ಪಡೆಯಬಹುದು) ಎಲ್ಲಾ ನಂತರದ ಸಂಕಲನಗಳು ಮಧ್ಯಂತರದ ಹೊರಗಿರುತ್ತವೆ [x-1, x+1]). ಆದ್ದರಿಂದ 1 - 2 + 3 - 4 + ... ವಿಭಿನ್ನವಾಗಿದೆ.

1, -2, 3, -4, 5, -6, ... ಪದಗಳು ಸರಳವಾದ ವಿಧಾನಕ್ಕೆ ಅನುಗುಣವಾಗಿರುವುದರಿಂದ, ಸರಣಿ 1 - 2 + 3 - 4 + ... ಹೋಗಬಹುದು. ಒಂದು ಸಾಮಾನ್ಯ ಸಂಖ್ಯೆ s ಗೆ s = 1 - 2 + 3 - 4 + ... ಬರೆಯಲು ಸಾಧ್ಯವಾದರೆ, s = 1⁄4 ಸರಣಿಯ ಮೊತ್ತವನ್ನು ಸಾಬೀತುಪಡಿಸಬಹುದು:[3] $${\displaystyle {\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+(1-2)+(3-4+5-6\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}-1+(3-4+5-6\cdots )\\&=&1+&(1-2+3-4+\cdots )&{}+(-2+3-4+5+\cdots )&{}+(-2+3-4+5+\cdots ))&{}+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&{}+(-2+3+3-4)&{}+(3-4-4+5)&{}+(-4+5)+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}$$

ಆದ್ದರಿಂದ ${\displaystyle s={\frac {1}{4}$.

1 - 2 + 3 - 4 + ... ಸಾಮಾನ್ಯ ಅರ್ಥದಲ್ಲಿ ಸಂಕ್ಷೇಪಿಸಲಾಗದಿದ್ದರೂ, s = 1 − 2 + 3 - 4 + ... = 1⁄4 ಎಂಬ ಸಮೀಕರಣವು 'ಅಂತಹ ಮೊತ್ತವಾಗಿದ್ದರೆ' ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಇದನ್ನು ಬೆಂಬಲಿಸಬಹುದು ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. ವಿಭಿನ್ನ ಸರಣಿಯ "ಮೊತ್ತ" ದ ವಿಶಾಲವಾದ ವ್ಯಾಖ್ಯಾನವನ್ನು ಸಂಕಲನ ವಿಧಾನ ಅಥವಾ ಸಂಕಲನ ವಿಧಾನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಇದು ಎಲ್ಲಾ ಸಂಭಾವ್ಯ ವರ್ಗಗಳ ಕೆಲವು ಉಪವಿಭಾಗಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸುತ್ತದೆ. ಸರಳ ಸಂಗ್ರಹಗಳನ್ನು ಪ್ರದರ್ಶಿಸಲು ವಿವಿಧ ವಿಧಾನಗಳಿವೆ (ಕೆಲವು ಕೆಳಗೆ ವಿವರಿಸಲಾಗಿದೆ). ಮೇಲಿನ ಚರ್ಚೆಯಿಂದ ಸ್ಥಿರತೆ ಮತ್ತು ರೇಖಾತ್ಮಕತೆ ಮತ್ತು ಸರಣಿ 1 − 2 + 3 - 4 + ... ನೀಡಿದ ಸಾರಾಂಶ ವಿಧಾನದಿಂದ, ಫಲಿತಾಂಶದ ಮೌಲ್ಯವು 1⁄4 ಆಗಿರುತ್ತದೆ ಎಂದು ಸಾಬೀತಾಗಿದೆ.[4] ಜೊತೆಗೆ, ರಿಂದ $${\displaystyle {\begin{array}{rcllll}2s&=&&(1-2+3-4+\cdots )&+&(1-2+3-4+\cdots )\\&=&1+{}&(-2+3-4+\cdots )&{}+1-2&{}+(3-4+5\cdots )\\&=&0+{}&(-2+3)+(3-4)+(-4+5)+\cdots \\2s&=&&1-1+1-1\cdots \end{array}$$ ಗ್ರಾಂಡಿ ಸರಣಿ 1 − 1 + 1 - 1 + ... = 1⁄2 ಅನ್ನು ಅಂತಹ ವಿಧಾನಗಳೊಂದಿಗೆ ಕೂಡಿಸಬಹುದು.[5]

1891 ರಲ್ಲಿ, ಅರ್ನೆಸ್ಟೊ ಸೆಸ್ರೊ ಅವರು ವಿಭಿನ್ನ ಸರಣಿಗಳನ್ನು ಕಲನಶಾಸ್ತ್ರಕ್ಕೆ ಕಟ್ಟುನಿಟ್ಟಾಗಿ ತರಲಾಗುವುದು ಎಂದು ಭರವಸೆ ವ್ಯಕ್ತಪಡಿಸಿದರು, "ಒಬ್ಬ ಈಗಾಗಲೇ (1 - 1 + 1 - 1 + ...) 2 = 1 - 2 + 3 - 4 + ... ಮತ್ತು ಎರಡೂ ಬದಿಗಳು 1⁄4 ಗೆ ಸಮಾನವಾಗಿವೆ ಎಂದು ಪ್ರತಿಪಾದಿಸುತ್ತದೆ."[5] ಸೆಸಾರೊಗೆ, ಈ ಸಮೀಕರಣವು ಅವರು ಹಿಂದಿನ ವರ್ಷ ಪ್ರಕಟಿಸಿದ ಪ್ರಮೇಯದ ಅನ್ವಯವಾಗಿದೆ, ಇದು ಸಂಕಲಿಸಬಹುದಾದ ವಿಭಿನ್ನ ಸರಣಿಯ ಇತಿಹಾಸದಲ್ಲಿ ಮೊದಲ ಪ್ರಮೇಯವಾಗಿದೆ.[1 ] ಅವರ ಸಂಕಲನ ವಿಧಾನದ ವಿವರಗಳು ಕೆಳಗಿವೆ; 1 - 2 + 3 - 4 + ... ಎಂಬುದು 1 - 1 + 1 - 1 + ... ಜೊತೆಗೆ 1 - 1 + 1 - 1 + ... ನ ಕೌಚಿ ಗುಣಲಬ್ಧ (ಡಿಸ್ಕ್ರೀಟ್ ಕನ್ವಲ್ಯೂಷನ್) ಎಂಬುದು ಕೇಂದ್ರ ಕಲ್ಪನೆಯಾಗಿದೆ. ಇವೆರಡೂ ಭಿನ್ನವಾಗಿದ್ದರೂ ಸಹ ಎರಡು ಅನಂತ ಸರಣಿಗಳ ಕೌಚಿ ಗುಣಲಬ್ಧವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗುತ್ತದೆ. Σa_n = Σb_n = Σ(−1)ⁿ ಸಂದರ್ಭದಲ್ಲಿ, ಕೌಚಿ ಗುಣಲಬ್ಧದ ನಿಯಮಗಳನ್ನು ಸೀಮಿತ ಕರ್ಣೀಯ ಮೊತ್ತಗಳಿಂದ ನೀಡಲಾಗುತ್ತದೆ $${\displaystyle {\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}$$ ಗುಣಲಬ್ಧ ಸರಣಿಯು ನಂತರ $${\displaystyle \sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\cdots .}$$ ಹೀಗೆ ಎರಡು ಸರಣಿಗಳ ಕೌಚಿ ಗುಣಲಬ್ಧವನ್ನು ಗೌರವಿಸುವ ಒಂದು ಸಂಕಲನ ವಿಧಾನವು - ಮತ್ತು ಸರಣಿ 1 - 1 + 1 - 1 + ... ಮೊತ್ತ 1/2 ಗೆ ನಿಯೋಜಿಸುತ್ತದೆ - 1 - 2 + 3 - 4 + ಸರಣಿಗೆ ಸಹ ನಿಯೋಜಿಸುತ್ತದೆ. .. ಮೊತ್ತ 1/4. ಹಿಂದಿನ ವಿಭಾಗದ ಫಲಿತಾಂಶದೊಂದಿಗೆ, ಇದು 1 - 1 + 1 - 1 + ... ಮತ್ತು 1 - 2 + 3 - 4 + ... ನ ಸಾರಾಂಶದ ನಡುವಿನ ಸಮಾನತೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ, ಇದು ರೇಖೀಯ, ಸ್ಥಿರ ಮತ್ತು ಕೌಚಿಯನ್ನು ಗೌರವಿಸುವ ವಿಧಾನಗಳೊಂದಿಗೆ ಗುಣಲಬ್ಧ. ಸೆಸಾರೊನ ಪ್ರಮೇಯವು ಒಂದು ಸೂಕ್ಷ್ಮ ಉದಾಹರಣೆಯಾಗಿದೆ. ಸರಣಿ 1 - 1 + 1 - 1 + ... ದುರ್ಬಲ ಅರ್ಥದಲ್ಲಿ ಸೆಸ್ರೊ-ಸಂಗ್ರಹಿಸಬಹುದಾದ, (C, 1)-ಸಂಗ್ರಹಿಸಬಹುದಾದ, ಆದರೆ 1 - 2 + 3 - 4 + ... ಗೆ ಸೆಸ್ರೊನ ಪ್ರಮೇಯದ ಬಲವಾದ ರೂಪದ ಅಗತ್ಯವಿದೆ. ,[6] (C, 2)-ಸಂಗ್ರಹಿಸಬಹುದಾದ. ಸೆಸಾರೊನ ಪ್ರಮೇಯದ ಎಲ್ಲಾ ರೂಪಗಳು ರೇಖೀಯ ಮತ್ತು ಸ್ಥಿರವಾಗಿರುವುದರಿಂದ,[7] ಮೊತ್ತಗಳ ಮೌಲ್ಯಗಳು ಮೇಲೆ ಲೆಕ್ಕ ಹಾಕಿದಂತೆ.

1 - 2 + 3 - 4 + ... ನ (C, 1) Cesàro ಮೊತ್ತವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಅದು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೆ, ಸರಣಿಯ ಭಾಗಶಃ ಮೊತ್ತಗಳ ಅಂಕಗಣಿತದ ವಿಧಾನಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಬೇಕಾಗುತ್ತದೆ. ಭಾಗಶಃ ಮೊತ್ತಗಳು: 1, −1, 2, −2, 3, −3, ..., ಮತ್ತು ಈ ಭಾಗಶಃ ಮೊತ್ತಗಳ ಅಂಕಗಣಿತದ ವಿಧಾನಗಳು: 1, 0, 2⁄3, 0, 3⁄5, 0, 4⁄7, .... ಸಾಧನಗಳ ಈ ಅನುಕ್ರಮವು ಒಮ್ಮುಖವಾಗುವುದಿಲ್ಲ, ಆದ್ದರಿಂದ 1 - 2 + 3 - 4 + ... Cesàro ಸಾರಾಂಶವಲ್ಲ.

Cesàro ಸಂಕಲನದ ಎರಡು ಪ್ರಸಿದ್ಧ ಸಾಮಾನ್ಯೀಕರಣಗಳಿವೆ: ಇವುಗಳಲ್ಲಿ ಕಲ್ಪನಾತ್ಮಕವಾಗಿ ಸರಳವಾದದ್ದು ನೈಸರ್ಗಿಕ ಸಂಖ್ಯೆಗಳಿಗೆ (H, n) ವಿಧಾನಗಳ ಅನುಕ್ರಮವಾಗಿದೆ n. (H, 1) ಮೊತ್ತವು Cesàro ಸಂಕಲನವಾಗಿದೆ, ಮತ್ತು ಹೆಚ್ಚಿನ ವಿಧಾನಗಳು ಸಾಧನಗಳ ಲೆಕ್ಕಾಚಾರವನ್ನು ಪುನರಾವರ್ತಿಸುತ್ತವೆ. ಮೇಲೆ, ಸಮ ಅರ್ಥವು 1⁄2 ಗೆ ಒಮ್ಮುಖವಾಗುತ್ತದೆ, ಆದರೆ ಬೆಸ ಸಾಧನಗಳು ಎಲ್ಲಾ 0 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ ಸಾಧನದ ಸಾಧನಗಳು ಸರಾಸರಿ 0 ಮತ್ತು 1⁄2 ಗೆ ಒಮ್ಮುಖವಾಗುತ್ತವೆ, ಅವುಗಳೆಂದರೆ 1⁄4.[8] ಆದ್ದರಿಂದ 1 - 2 + 3 - 4 + ... (H, 2) 1⁄4 ಗೆ ಸಂಕ್ಷೇಪಿಸುತ್ತದೆ.

"H" ಎಂಬುದು ಒಟ್ಟೊ ಹೋಲ್ಡರ್ ಅನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ, ಅವರು 1882 ರಲ್ಲಿ ಗಣಿತಜ್ಞರು ಈಗ ಅಬೆಲ್ ಸಂಕಲನ ಮತ್ತು (H, n) ಸಂಕಲನದ ನಡುವಿನ ಸಂಪರ್ಕವನ್ನು ಏನು ಎಂದು ಸಾಬೀತುಪಡಿಸಿದರು; 1 - 2 + 3 - 4 + ... ಅವನ ಮೊದಲ ಉದಾಹರಣೆಯಾಗಿದೆ.[9] 1⁄4 ಎಂಬುದು 1 - 2 + 3 - 4 + ... ನ (H, 2) ಮೊತ್ತವಾಗಿದೆ ಎಂಬ ಅಂಶವು ಅಬೆಲ್ ಮೊತ್ತವೂ ಆಗಿದೆ ಎಂದು ಖಾತರಿಪಡಿಸುತ್ತದೆ; ಇದನ್ನು ನೇರವಾಗಿ ಕೆಳಗೆ ಸಾಬೀತುಪಡಿಸಲಾಗುತ್ತದೆ.

Cesàro ಸಂಕಲನದ ಇತರ ಸಾಮಾನ್ಯವಾಗಿ ರೂಪಿಸಲಾದ ಸಾಮಾನ್ಯೀಕರಣವು (C, n) ವಿಧಾನಗಳ ಅನುಕ್ರಮವಾಗಿದೆ. (C, n) ಸಂಕಲನ ಮತ್ತು (H, n) ಸಂಕಲನವು ಯಾವಾಗಲೂ ಒಂದೇ ಫಲಿತಾಂಶಗಳನ್ನು ನೀಡುತ್ತದೆ ಎಂದು ಸಾಬೀತಾಗಿದೆ, ಆದರೆ ಅವು ವಿಭಿನ್ನ ಐತಿಹಾಸಿಕ ಹಿನ್ನೆಲೆಗಳನ್ನು ಹೊಂದಿವೆ. 1887 ರಲ್ಲಿ, Cesàro (C, n) ಸಂಕಲನದ ವ್ಯಾಖ್ಯಾನವನ್ನು ಹೇಳುವ ಹತ್ತಿರ ಬಂದರು, ಆದರೆ ಅವರು ಕೆಲವೇ ಉದಾಹರಣೆಗಳನ್ನು ನೀಡಿದರು. ನಿರ್ದಿಷ್ಟವಾಗಿ ಹೇಳುವುದಾದರೆ, ಅವರು 1 − 2 + 3 - 4 + ..., ಗೆ 1⁄4 ಅನ್ನು (C, n) ಎಂದು ಮರುಹೊಂದಿಸಬಹುದಾದ ವಿಧಾನದಿಂದ ಒಟ್ಟುಗೂಡಿಸಿದರು ಆದರೆ ಆ ಸಮಯದಲ್ಲಿ ಅದನ್ನು ಸಮರ್ಥಿಸಲಾಗಿಲ್ಲ. ಒಂದು (C, n)-ಸಂಗ್ರಹಿಸಬಹುದಾದ ಸರಣಿ ಮತ್ತು (C, m)-ಸಂಗ್ರಹಿಸಬಹುದಾದ ಸರಣಿಯ ಕೌಚಿ ಉತ್ಪನ್ನವು (C, m + n +1)ಸಂಗ್ರಹಿಸಬಹುದು ಎಂದು ತನ್ನ ಪ್ರಮೇಯವನ್ನು ಹೇಳಲು ಅವರು 1890 ರಲ್ಲಿ (C, n) ವಿಧಾನಗಳನ್ನು ಔಪಚಾರಿಕವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಿದರು. .[10]

1749 ರ ವರದಿಯಲ್ಲಿ, ಲಿಯೊನ್ಹಾರ್ಡ್ ಯೂಲರ್ ಸರಣಿಯು ಭಿನ್ನವಾಗಿದೆ ಎಂದು ಒಪ್ಪಿಕೊಳ್ಳುತ್ತಾನೆ ಆದರೆ ಹೇಗಾದರೂ ಅದನ್ನು ಒಟ್ಟುಗೂಡಿಸಲು ಸಿದ್ಧಪಡಿಸುತ್ತಾನೆ:

... ಈ ಸರಣಿಯ 1 - 2 + 3 - 4 + 5 - 6 ಇತ್ಯಾದಿಗಳ ಮೊತ್ತವು 1⁄4 ಎಂದು ಹೇಳಿದಾಗ, ಅದು ವಿರೋಧಾಭಾಸವಾಗಿ ಕಾಣಿಸಬೇಕು. ಈ ಸರಣಿಯ 100 ಪದಗಳನ್ನು ಸೇರಿಸುವ ಮೂಲಕ, ನಾವು −50 ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ, ಆದಾಗ್ಯೂ, 101 ಪದಗಳ ಮೊತ್ತವು +51 ಅನ್ನು ನೀಡುತ್ತದೆ, ಇದು 1⁄4 ಕ್ಕಿಂತ ಭಿನ್ನವಾಗಿದೆ ಮತ್ತು ಪದಗಳ ಸಂಖ್ಯೆಯನ್ನು ಹೆಚ್ಚಿಸಿದಾಗ ಇನ್ನೂ ಹೆಚ್ಚಾಗುತ್ತದೆ. ಆದರೆ ಮೊತ್ತ ಎಂಬ ಪದಕ್ಕೆ ಹೆಚ್ಚು ವಿಸ್ತೃತ ಅರ್ಥವನ್ನು ನೀಡುವುದು ಅವಶ್ಯಕ ಎಂದು ನಾನು ಈಗಾಗಲೇ ಹಿಂದಿನ ಸಮಯದಲ್ಲಿ ಗಮನಿಸಿದ್ದೇನೆ ...^[೧]

ಯೂಲರ್ ಹಲವಾರು ಬಾರಿ "ಮೊತ್ತ" ಪದದ ಸಾಮಾನ್ಯೀಕರಣವನ್ನು ಪ್ರಸ್ತಾಪಿಸಿದರು. 1 - 2 + 3 - 4 + ... ಪ್ರಕರಣದಲ್ಲಿ, ಅವನ ಆಲೋಚನೆಗಳು ಈಗ ಅಬೆಲ್ ಸಂಕಲನ ಎಂದು ಕರೆಯಲ್ಪಡುವಂತೆಯೇ ಇರುತ್ತವೆ:

...  ಈ ಸರಣಿಯ 1 - 2 + 3 - 4 + 5 ಇತ್ಯಾದಿಗಳ ಮೊತ್ತವು 1⁄4 ಆಗಿರುವುದು ಅನುಮಾನವೇನಲ್ಲ; ಏಕೆಂದರೆ ಇದು 1⁄(1+1)² ಸೂತ್ರದ ವಿಸ್ತರಣೆಯಿಂದ ಉದ್ಭವಿಸುತ್ತದೆ, ಇದರ ಮೌಲ್ಯವು ಅವಿರೋಧವಾಗಿ 1⁄4 ಆಗಿದೆ. ಸಾಮಾನ್ಯ ಸರಣಿ 1 − 2x + 3x² − 4x³ + 5x⁴ − 6x⁵ + &c. ಅನ್ನು ಪರಿಗಣಿಸುವ ಮೂಲಕ ಕಲ್ಪನೆಯು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ. 1⁄(1+x)² ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ವಿಸ್ತರಿಸುವಾಗ ಅದು ಉದ್ಭವಿಸುತ್ತದೆ, ನಾವು x = 1 ಅನ್ನು ಹೊಂದಿಸಿದ ನಂತರ ಈ ಸರಣಿಯು ನಿಜವಾಗಿ ಸಮಾನವಾಗಿರುತ್ತದೆ.[12] ^[೨]

ಅದನ್ನು ನೋಡಲು ಹಲವು ಮಾರ್ಗಗಳಿವೆ, ಕನಿಷ್ಠ ಸಂಪೂರ್ಣ ಮೌಲ್ಯಗಳಿಗೆ |x| < 1, ಅದರಲ್ಲಿ ಯೂಲರ್ ಸರಿ $${\displaystyle 1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}.}$$ ಒಬ್ಬರು ಬಲಭಾಗದ ಟೇಲರ್ ವಿಸ್ತರಣೆಯನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು ಅಥವಾ ಬಹುಪದಗಳಿಗೆ ಔಪಚಾರಿಕ ದೀರ್ಘ ವಿಭಜನೆ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಅನ್ವಯಿಸಬಹುದು. ಎಡಭಾಗದಿಂದ ಪ್ರಾರಂಭಿಸಿ, ಮೇಲಿನ ಸಾಮಾನ್ಯ ಹ್ಯೂರಿಸ್ಟಿಕ್ಸ್ ಅನ್ನು ಅನುಸರಿಸಿ ಮತ್ತು (1 + x) ಎರಡು ಬಾರಿ ಗುಣಿಸಲು ಪ್ರಯತ್ನಿಸಬಹುದು ಅಥವಾ ಜ್ಯಾಮಿತೀಯ ಸರಣಿ 1 - x + x2 - ವರ್ಗೀಕರಿಸಲು ಪ್ರಯತ್ನಿಸಬಹುದು .... ಯೂಲರ್ ನಂತರದ ಸರಣಿಯ ಪದವನ್ನು ಪ್ರತ್ಯೇಕಿಸಲು ಸಲಹೆ ನೀಡುವಂತೆ ತೋರುತ್ತದೆ. ಅವಧಿಯ ಪ್ರಕಾರ.[13] ಆಧುನಿಕ ದೃಷ್ಟಿಯಲ್ಲಿ, ಉತ್ಪಾದಿಸುವ ಕಾರ್ಯ 1 - 2x + 3x2 - 4x3 + ... x = 1 ನಲ್ಲಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುವುದಿಲ್ಲ, ಆದ್ದರಿಂದ ಫಲಿತಾಂಶದ ಅಭಿವ್ಯಕ್ತಿಗೆ ಮೌಲ್ಯವನ್ನು ಸರಳವಾಗಿ ಬದಲಿಸಲಾಗುವುದಿಲ್ಲ. ಎಲ್ಲಾ |x| < 1 ಗೆ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆಯಾದ್ದರಿಂದ, x 1 ರ ಸಮೀಪಿಸುತ್ತಿರುವಂತೆ ಇನ್ನೂ ಮಿತಿಯನ್ನು ತೆಗೆದುಕೊಳ್ಳಬಹುದು ಮತ್ತು ಇದು ಅಬೆಲ್ ಮೊತ್ತದ ವ್ಯಾಖ್ಯಾನವಾಗಿದೆ: $${\displaystyle \lim _{x\rightarrow 1^{-}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1^{-}{\frac {1}{(1+x)^{2}={\frac {1}{4}.}$$

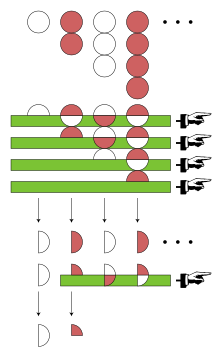
ಯೂಲರ್ ಸರಣಿಗೆ ಮತ್ತೊಂದು ತಂತ್ರವನ್ನು ಅನ್ವಯಿಸಿದರು: ಯೂಲರ್ ರೂಪಾಂತರ, ಅವರ ಸ್ವಂತ ಆವಿಷ್ಕಾರಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ. ಯೂಲರ್ ರೂಪಾಂತರವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು, ಪರ್ಯಾಯ ಸರಣಿಯನ್ನು ರೂಪಿಸುವ ಧನಾತ್ಮಕ ಪದಗಳ ಅನುಕ್ರಮದೊಂದಿಗೆ ಪ್ರಾರಂಭವಾಗುತ್ತದೆ-ಈ ಸಂದರ್ಭದಲ್ಲಿ 1, 2, 3, 4, .... ಈ ಅನುಕ್ರಮದ ಮೊದಲ ಅಂಶವನ್ನು ಲೇಬಲ್ ಮಾಡಲಾಗಿದೆ a₀.

ಮುಂದೆ 1, 2, 3, 4, ... ನಡುವೆ ಫಾರ್ವರ್ಡ್ ವ್ಯತ್ಯಾಸಗಳು ಅನುಕ್ರಮದ ಅಗತ್ಯವಿದೆ; ಇದು ಕೇವಲ 1, 1, 1, 1, .... ಈ ಅನುಕ್ರಮದ ಮೊದಲ ಅಂಶವನ್ನು Δa₀ ಎಂದು ಲೇಬಲ್ ಮಾಡಲಾಗಿದೆ. ಯೂಲರ್ ರೂಪಾಂತರವು ವ್ಯತ್ಯಾಸಗಳ ವ್ಯತ್ಯಾಸಗಳನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ, ಮತ್ತು ಹೆಚ್ಚಿನ ಪುನರಾವರ್ತನೆಗಳು, ಆದರೆ 1, 1, 1, 1, ... ನಡುವಿನ ಎಲ್ಲಾ ಫಾರ್ವರ್ಡ್ ವ್ಯತ್ಯಾಸಗಳು 0. ದಿ ಯೂಲರ್ ರೂಪಾಂತರ 1 − 2 + 3 - 4 + ... ನಂತರ ಹೀಗೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ $${\displaystyle {\frac {1}{2}a_{0}-{\frac {1}{4}\Delta a_{0}+{\frac {1}{8}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}-{\frac {1}{4}.}$$ ಆಧುನಿಕ ಪರಿಭಾಷೆಯಲ್ಲಿ, 1 − 2 + 3 - 4 + ... ಯೂಲರ್ ಸಾರಾಂಶ ಗೆ 1⁄4 ಎಂದು ಒಬ್ಬರು ಹೇಳುತ್ತಾರೆ.

ಯೂಲರ್ ಸಾರಾಂಶವು ಬೋರೆಲ್ ಸಮ್ಮಬಿಲಿಟಿ ಅನ್ನು ಸಹ ಸೂಚಿಸುತ್ತದೆ, ಅದೇ ಸಂಕಲನ ಮೌಲ್ಯದೊಂದಿಗೆ, ಅದು ಸಾಮಾನ್ಯವಾಗಿ ಮಾಡುತ್ತದೆ.^[೩]

ಕೇವಲ ಎರಡು ಭೌತಿಕ ತತ್ವಗಳನ್ನು ಅನ್ವಯಿಸುವ ಮೂಲಕ 1 − 2 + 3 − 4 + ... = 1⁄4 ಗೆ ಸೈಚೆವ್ ಮತ್ತು ವೊಯ್ಸಿಸ್ಕಿ ಆಗಮಿಸುತ್ತಾರೆ: ಅನಂತವಾದ ವಿಶ್ರಾಂತಿ ಮತ್ತು ಮಾಪಕಗಳ ಪ್ರತ್ಯೇಕತೆ. ನಿಖರವಾಗಿ ಹೇಳಬೇಕೆಂದರೆ, ಈ ತತ್ವಗಳು "φ-ಸಂಗ್ರಹ ವಿಧಾನಗಳ" ಒಂದು ವಿಶಾಲವಾದ ಕುಟುಂಬವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲು ಕಾರಣವಾಗುತ್ತವೆ, ಇವೆಲ್ಲವೂ ಸರಣಿಯನ್ನು 1⁄4 ಗೆ ಒಟ್ಟುಗೂಡಿಸುತ್ತವೆ:

• φ(x) ಒಂದು ಫಂಕ್ಷನ್ ಆಗಿದ್ದರೆ ಅದರ ಮೊದಲ ಮತ್ತು ಎರಡನೆಯ ವ್ಯುತ್ಪನ್ನಗಳು ನಿರಂತರವಾಗಿ ಮತ್ತು (0, ∞) ಗಿಂತ ಇಂಟಿಗ್ರಬಲ್ ಆಗಿದ್ದರೆ, ಅಂದರೆ φ(0) = 1 ಮತ್ತು φ(x ನ ಮಿತಿಗಳು ) ಮತ್ತು +∞ ನಲ್ಲಿ xφ(x) ಎರಡೂ 0 ಆಗಿರುತ್ತವೆ, ನಂತರ^[೪] $${\displaystyle \lim _{\delta \rightarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}.}$$

ಈ ಫಲಿತಾಂಶವು ಅಬೆಲ್ ಸಂಕಲನವನ್ನು ಸಾಮಾನ್ಯೀಕರಿಸುತ್ತದೆ, ಇದನ್ನು φ(x) = exp(−x) ಎಂದು ಬಿಡುವ ಮೂಲಕ ಮರುಪಡೆಯಲಾಗುತ್ತದೆ. ಸಾಮಾನ್ಯ ಹೇಳಿಕೆಯನ್ನು ಸರಣಿಯಲ್ಲಿನ ಪದಗಳನ್ನು m ಮೇಲೆ ಜೋಡಿಸುವ ಮೂಲಕ ಮತ್ತು ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ರೀಮನ್ ಅವಿಭಾಜ್ಯ ಆಗಿ ಪರಿವರ್ತಿಸುವ ಮೂಲಕ ಸಾಬೀತುಪಡಿಸಬಹುದು. ನಂತರದ ಹಂತಕ್ಕೆ, 1 - 1 + 1 - 1 + ... ಗಾಗಿ ಅನುಗುಣವಾದ ಪುರಾವೆ ಸರಾಸರಿ ಮೌಲ್ಯ ಪ್ರಮೇಯ ಅನ್ವಯಿಸುತ್ತದೆ, ಆದರೆ ಇಲ್ಲಿ ಒಬ್ಬರಿಗೆ ಟೇಲರ್‌ನ ಪ್ರಮೇಯ ಪ್ರಬಲವಾದ ಲ್ಯಾಗ್ರೇಂಜ್ ರೂಪದ ಅಗತ್ಯವಿದೆ.

1 - 1 + 1 - 1 + ... ನ ಮೂರು ಪಟ್ಟು ಕೌಚಿ ಉತ್ಪನ್ನವು 1 − 3 + 6 - 10 + ..., ತ್ರಿಕೋನ ಸಂಖ್ಯೆಯಗಳು; ಅದರ ಅಬೆಲ್ ಮತ್ತು ಯೂಲರ್ ಮೊತ್ತ 1⁄8.^[೫] 1 − 1 + 1 - 1 + ... ನ ನಾಲ್ಕು ಪಟ್ಟು ಕೌಚಿ ಉತ್ಪನ್ನವು 1 − 4 + 10 − 20 + ..., ಪರ್ಯಾಯ ಸರಣಿಯಾಗಿದೆ. ಟೆಟ್ರಾಹೆಡ್ರಲ್ ಸಂಖ್ಯೆಗಳ, ಇದರ ಅಬೆಲ್ ಮೊತ್ತ 1⁄16.

1 − 2 + 3 - 4 + ... ನ ಮತ್ತೊಂದು ಸಾಮಾನ್ಯೀಕರಣವು ಸ್ವಲ್ಪ ವಿಭಿನ್ನ ದಿಕ್ಕಿನಲ್ಲಿ 1 − 2ⁿ + 3ⁿ − 4ⁿ + ... n ನ ಇತರ ಮೌಲ್ಯಗಳಿಗಾಗಿ ಧನಾತ್ಮಕ ಪೂರ್ಣಾಂಕಗಳಿಗೆ n, ಈ ಸರಣಿಗಳು ಕೆಳಗಿನ ಅಬೆಲ್ ಮೊತ್ತವನ್ನು ಹೊಂದಿವೆ:^[೬] $${\displaystyle 1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}B_{n}$$

ಇಲ್ಲಿ B_n ಎಂದರೆ ಬರ್ನೌಲಿ ಸಂಖ್ಯೆಗಳು. "n" ಗೆ ಸಹ, ಇದು ಕಡಿಮೆಯಾಗುತ್ತದೆ $${\displaystyle 1-2^{2k}+3^{2k}-\cdots =0,}$$ ರೀಮನ್ ಝೀಟಾ ಫಂಕ್ಷನ್ ನ ಋಣಾತ್ಮಕ ಸಮ ಮೌಲ್ಯಗಳು ಶೂನ್ಯ ಎಂದು ಹೇಳುವುದನ್ನು ಅರ್ಥೈಸಬಹುದು. ಈ ಮೊತ್ತವು 1826 ರಲ್ಲಿ ನೀಲ್ಸ್ ಹೆನ್ರಿಕ್ ಅಬೆಲ್ ನಿಂದ ನಿರ್ದಿಷ್ಟ ಅಪಹಾಸ್ಯಕ್ಕೆ ಗುರಿಯಾಯಿತು:

ವಿಭಿನ್ನ ಸರಣಿಗಳು ಇಡೀ ದೆವ್ವದ ಕೆಲಸದಲ್ಲಿವೆ ಮತ್ತು ಅವುಗಳಲ್ಲಿ ಯಾವುದೇ ಪುರಾವೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು ಒಬ್ಬರು ಧೈರ್ಯಮಾಡುವುದು ನಾಚಿಕೆಗೇಡಿನ ಸಂಗತಿಯಾಗಿದೆ. ಇವುಗಳನ್ನು ಬಳಸಿಕೊಂಡರೆ ತನಗೆ ಬೇಕಾದುದನ್ನು ಪಡೆಯಬಹುದು, ಮತ್ತು ಅದು ತುಂಬಾ ಅತೃಪ್ತಿ ಮತ್ತು ಹಲವಾರು ವಿರೋಧಾಭಾಸಗಳನ್ನು ಮಾಡಿದೆ. ಹಾಗೆ ಹೇಳುವುದಕ್ಕಿಂತ ಹೆಚ್ಚು ಭಯಾನಕವಾದದ್ದನ್ನು ಯಾರಾದರೂ ಯೋಚಿಸಬಹುದೇ?

0 = 1 − 2²ⁿ + 3²ⁿ − 4²ⁿ + etc.

ಇಲ್ಲಿ n ಎಂಬುದು ಧನಾತ್ಮಕ ಸಂಖ್ಯೆ. ಸ್ನೇಹಿತರೇ ನಗುವ ವಿಷಯ ಇಲ್ಲಿದೆ.^[೭]

ಸೆಸಾರೊನ ಶಿಕ್ಷಕ, ಯುಜೀನ್ ಚಾರ್ಲ್ಸ್ ಕ್ಯಾಟಲನ್ ಕೂಡ ವಿಭಿನ್ನ ಸರಣಿಗಳನ್ನು ತಿರಸ್ಕರಿಸಿದರು. ಕ್ಯಾಟಲಾನ್‌ನ ಪ್ರಭಾವದ ಅಡಿಯಲ್ಲಿ, ಸೆಸ್ರೊ ಆರಂಭದಲ್ಲಿ "ಸಾಂಪ್ರದಾಯಿಕ ಸೂತ್ರಗಳನ್ನು" 1 − 2ⁿ + 3ⁿ − 4ⁿ + ... "ಅಸಂಬದ್ಧ ಸಮಾನತೆಗಳು" ಎಂದು ಉಲ್ಲೇಖಿಸಿದರು, ಮತ್ತು 1883 ರಲ್ಲಿ ಸೆಸಾರೊ ಆ ಕಾಲದ ವಿಶಿಷ್ಟ ದೃಷ್ಟಿಕೋನವನ್ನು ವ್ಯಕ್ತಪಡಿಸಿದ ಸೂತ್ರಗಳು ಸುಳ್ಳು ಆದರೆ ಇನ್ನೂ ಹೇಗಾದರೂ ಔಪಚಾರಿಕವಾಗಿ ಉಪಯುಕ್ತವಾಗಿವೆ. ಅಂತಿಮವಾಗಿ, ಅವರ 1890 ರ ಸುರ್ ಲಾ ಮಲ್ಟಿಪ್ಲಿಕೇಶನ್ ಡೆಸ್ ಸೀರೀಸ್ ನಲ್ಲಿ, ಸೆಸಾರೊ ವ್ಯಾಖ್ಯಾನಗಳಿಂದ ಪ್ರಾರಂಭವಾಗುವ ಆಧುನಿಕ ವಿಧಾನವನ್ನು ತೆಗೆದುಕೊಂಡರು.^[೮]

"n" ನ ಪೂರ್ಣಾಂಕವಲ್ಲದ ಮೌಲ್ಯಗಳಿಗಾಗಿ ಸರಣಿಗಳನ್ನು ಸಹ ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ; ಇವುಗಳು ಡಿರಿಚ್ಲೆಟ್ ಎಟಾ ಫಂಕ್ಷನ್ ಅನ್ನು ರೂಪಿಸುತ್ತವೆ. 1 − 2 + 3 - 4 + ... ಗೆ ಸಂಬಂಧಿಸಿದ ಸರಣಿಯನ್ನು ಅಧ್ಯಯನ ಮಾಡಲು ಯೂಲರ್‌ನ ಪ್ರೇರಣೆಯ ಭಾಗವು eta ಫಂಕ್ಷನ್‌ನ ಕ್ರಿಯಾತ್ಮಕ ಸಮೀಕರಣ ಆಗಿತ್ತು, ಇದು ನೇರವಾಗಿ ನ ಕ್ರಿಯಾತ್ಮಕ ಸಮೀಕರಣಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ. ರೀಮನ್ ಝೀಟಾ ಫಂಕ್ಷನ್. ಯೂಲರ್ ಈಗಾಗಲೇ ಈ ಕಾರ್ಯಗಳ ಮೌಲ್ಯಗಳನ್ನು ಧನಾತ್ಮಕ ಸಮ ಪೂರ್ಣಾಂಕಗಳು (ಬಾಸೆಲ್ ಸಮಸ್ಯೆ ನಲ್ಲಿ ಕಂಡುಹಿಡಿಯುವಲ್ಲಿ ಪ್ರಸಿದ್ಧರಾಗಿದ್ದರು ಮತ್ತು ಅವರು ಧನಾತ್ಮಕ ಬೆಸ ಪೂರ್ಣಾಂಕಗಳು (ಅಪೆರಿಯ ಸ್ಥಿರವನ್ನು ಒಳಗೊಂಡಂತೆ) ಹಾಗೆಯೇ, ಇಂದಿಗೂ ಅಸ್ಪಷ್ಟವಾಗಿ ಉಳಿದಿರುವ ಸಮಸ್ಯೆ. ನಿರ್ದಿಷ್ಟವಾಗಿ eta ಕಾರ್ಯವು ಯೂಲರ್‌ನ ವಿಧಾನಗಳಿಂದ ವ್ಯವಹರಿಸುವುದು ಸುಲಭವಾಗಿದೆ ಏಕೆಂದರೆ ಅದರ ಡಿರಿಚ್ಲೆಟ್ ಸರಣಿ ಅಬೆಲ್ ಎಲ್ಲೆಡೆಯೂ ಸಾರಾಂಶವಾಗಿದೆ; ಝೀಟಾ ಫಂಕ್ಷನ್‌ನ ಡಿರಿಚ್ಲೆಟ್ ಸರಣಿಯು ಅದು ಎಲ್ಲಿ ಬೇರೆಯಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ಒಟ್ಟುಗೂಡಿಸಲು ಕಷ್ಟವಾಗುತ್ತದೆ.^[೯] ಉದಾಹರಣೆಗೆ, 1 − 2 + 3 − 4 + ... ಝೀಟಾ ಫಂಕ್ಷನ್‌ನಲ್ಲಿ ಪರ್ಯಾಯವಲ್ಲದ ಸರಣಿಯು 1 + 2 + 3 + 4 + · · · ಆಧುನಿಕ ಭೌತಶಾಸ್ತ್ರ ನಲ್ಲಿ ಆಳವಾದ ಅನ್ವಯಿಕೆಗಳನ್ನು ಹೊಂದಿದೆ ಆದರೆ ಒಟ್ಟು ಮಾಡಲು ಹೆಚ್ಚು ಬಲವಾದ ವಿಧಾನಗಳ ಅಗತ್ಯವಿದೆ.

• 1 + 2 + 3 + 4 + ⋯
• 1 + 1 + 1 + 1 + ⋯
• 1 + 2 + 4 + 8 + ·...
• 1 - 2 + 4 - 8 + ⋯

ಟೆಂಪ್ಲೇಟು:Series (mathematics)