1 − 2 + 3 − 4 + · · ·

În analiza matematică, seria infinită 1 - 2 + 3 - 4 + … este o serie alternată ai cărei termeni sunt numerele întregi pozitive succesive. Folosind notația însumării, suma parțială a primilor m termeni ai seriei poate fi exprimată ca:
Seria infinită diverge, adică șirul său de sume parțiale, (1, −1, 2, −2, …), nu tinde înspre o limită finită. Astfel de serii nu au sumă în sensul uzual al noțiunii de ”sumă” a seriei, lucru clarificat încă din 1755 de Leonhard Euler, în Institutiones Calculi Differentialis. Euler avea să enunțe, în același secol al XVIII-lea, ceea ce în opinia lui era o egalitate paradoxală:
În fapt, Euler mai notează și alte egalități ”dincolo de puterea de înțelegere” :
Înainte de Cauchy, în locul întrebării ”Cum să definim 1 - 1 + 1 - 1 + 1... ?”, întrebarea firească folosită era ”Ce este o sumă precum 1 - 1 + 1 - 1 + 1... ?” ceea a condus, alături de o anumită perplexitate a minții, către discuții deseori foarte aprinse.
Către sfârșitul secolului al XIX-lea, metodele de sumare ale seriilor divergente au început să fie studiate sistematic, constituind o nouă ramură a matematicii. Începând cu 1890, Ernesto Cesàro, Émile Borel și alții au investigat metode clar definite de a atribui o „sumă generalizată” unor serii divergente. Astfel pot fi menționate transformarea liniară sau metodele Cesàro, Abel, Borel, Euler, Norlund, Riesz sau Riemann. Multe dintre aceste metode de sumare vor aloca pentru 1 − 2 + 3 − 4 + … valoarea de 1⁄4. Sumarea lui Cesàro este unul dintre procedeele care nu furnizează nicio valoare.
Seria 1 − 2 + 3 − 4 + … este strâns legată de seria lui Grandi, 1 − 1 + 1 − 1 + …. Euler le-a tratat pe acestea ca fiind cazuri particulare ale seriei 1 − 2n + 3n − 4n + … pentru n arbitrar, o direcție de cercetare care extinde activitatea sa asupra problemei Basel spre ecuațiile funcționale a ceea ce este cunoscut în prezent ca funcția eta Dirichlet și funcția zeta Riemann.
Divergența
Termenii seriei nu tind către 0; prin urmare, 1 − 2 + 3 − 4 + … diverge, conform primului criteriu de convergență pentru serii. Prin definiție, convergența sau divergența unei serii infinite este determinată de convergența sau divergența șirului de sume parțiale, iar în acest caz, sumele parțiale pentru 1 − 2 + 3 − 4 + … sunt:[1]
- 1 = 1,
- 1 − 2 = −1,
- 1 − 2 + 3 = 2,
- 1 − 2 + 3 − 4 = −2,
- 1 − 2 + 3 − 4 + 5 = 3,
- 1 − 2 + 3 − 4 + 5 − 6 = −3,
- …
Șirul Sm = (1, −1, 2, −2, 3, -3, …) arată clar că seria nu converge spre o anumită valoare (pentru orice limită x propusă, există drept exemplu[N 1] intervalul [x-1, x+1] o vecinătate a lui x în care nu se acumulează valorile lui Sm: pentru orice N număr natural se poate găsi un punct dincolo de aceasta pentru care suma parțială nu aparține intervalului fixat, [x-1, x+1]), deci seria 1 − 2 + 3 − 4 + … este divergentă.
Un rezultat colateral se obține observând că în timp ce termenii din stânga ai egalităților de mai sus parcurg numerele naturale, cei din dreapta parcurg numerele întregi. Dacă se adăugă în lista de egalități și suma parțială vidă, 0 = 0, se obține o corespondență biunivocă între numerele naturale și cele întregi și astfel se stabilește numărabilitatea mulțimii de numere întregi.[2]
Convergența
În cazul în care numerele implicate în serie sunt înțelese ca numere complexe, seria se poate scrie
Pentru aceasta, mulțimea a numerelor complexe trebuie completată cu numărul , devenind , sau, echivalent, planul complex se completează cu dreapta de la infinit, devenind planul proiectiv (sau sfera Riemann). În teoria speciilor acest procedeu se numește și „integrarea unei specii”
În acest caz seria poate fi considerată drept convergentă, iar suma ei este numărul .
Euristici pentru însumare
Liniaritate și stabilitate
O serie absolut convergentă rămâne convergentă, cu aceeași sumă, la orice reordonare sau regrupare a termenilor. Spre deosebire de acestea, seriile divergente pot fi reordonate și regrupate astfel încât să furnizeze rezultate diferite.
Dacă însă se restricționează operațiile posibile la acelea care satisfac două principii, numite de liniaritate și de stabilitate, care sunt dintre cele mai simple cerințe pentru o posibilă definire a ”sumei”, 1⁄4 va deveni cel mai întâlnit candidat pentru titlul de ”sumă” a seriei.
- Liniaritate (sumare termenilor corespondenți): [a1 + a2 + a3 + ... ] + [ b1 + b2 + b3 +...] = (a1 + b1) + (a2 + b2) + (a3 + b3) + ...
- Stabilitate (separarea primului termen ): a1 + a2 + a3 + ... = a1 + [a2 + a3 + ...]
Din moment ce termenii 1, −2, 3, −4, 5, −6, … urmează un tipar simplu, seria 1 − 2 + 3 − 4 + … poate fi manipulată prin separarea primului termen (stabilitate) și adunarea termenilor corespondenți (liniaritate) pentru a obține o valoare numerică. Următoarele calcule, folosind regulile de liniaritate și stabilitate, conduc la s = 1⁄4 :[N 2]

Deci, . Această derivare este ilustrată grafic în imaginea din dreapta.
Deși 1 − 2 + 3 − 4 + … nu are o sumă în sensul obișnuit, ecuația s = 1 − 2 + 3 − 4 + … = 1⁄4 poate fi considerată drept cea mai firească valoare a sumei seriei, în caz că această sumă trebuie definită. Întrucât există diverse procedee de a atribui unei serii o valoare care să-i corespundă drept sumă, acestea numindu-se metode de sumare (sau de însumare), studiul acestora se face pe baza proprietăților întâlnite la seriile convergente. Ce a fost demonstrat mai sus este afirmația: "Orice metodă de sumare liniară și stabilă va atribui seriei 1 − 2 + 3 − 4 + … suma 1⁄4." Mai mult, deoarece:
o astfel de metodă de sumare va atribui seriei lui Grandi suma 2s = 1⁄2 .
Unele dintre metodele de sumare ce pot fi folosite pentru seria de față sunt descrise mai jos.
Produsul Cauchy
În 1891, Ernesto Cesàro a exprimat speranța că seriile divergente ar putea fi riguros încadrate în analiza matematică, subliniind : „Putem deja scrie (1 − 1 + 1 − 1 + …)2 = 1 − 2 + 3 − 4 + … și afirma că ambele părți sunt egale cu 1⁄4.”[3] Pentru Cesàro, acestă ecuație rezulta prin aplicarea unei teoreme pe care o publicase cu un an mai devreme, și care poate fi socotită drept prima teoremă din istoria seriilor divergente sumabile. Detaliile metodei lui de însumare sunt arătate mai jos; ideea principală este că 1 − 2 + 3 − 4 + ... este produsul Cauchy al seriei lui Grandi, 1 − 1 + 1 − 1 + ..., cu ea însăși.
Produsul Cauchy a două serii infinite poate fi definit independent de convergența lor, prin formula termenului general al seriei-produs: . În cazul în care Σan = Σbn = Σ(−1)n, termenii produsului Cauchy sunt generați de sumele finite diagonale:
Atunci seria-produs este aceasta:
De aceea orice metodă de însumare compatibilă cu produsul Cauchy și care asignează 1 − 1 + 1 − 1 + ... = 1⁄2, va furniza totodată suma 1 − 2 + 3 − 4 + ... = 1⁄4. Împreună cu rezultatul obținut în secțiunea anterioară, rezultă echivalența sumabilității seriilor 1 − 1 + 1 − 1 + ... și 1 − 2 + 3 − 4 + ... prin metode liniare, stabile și care respectă produsul Cauchy (compatibile cu produsul Cauchy).
Metode specifice
Cesàro și Hölder

Pentru a găsi suma seriei 1 − 2 + 3 − 4 + ... conform metodei lui Cesàro (C, 1), dacă aceasta este definită, este necesar calculul mediilor aritmetice ale sumelor parțiale ale seriei. Sumele parțiale sunt:
- 1, −1, 2, −2, 3, −3, ...,
și mediile aritmetice ale acestor sume parțiale sunt:
- 1, 0, 2⁄3, 0, 3⁄5, 0, 4⁄7, ....
Acest șir nu converge (întrucât conține două subșiruri convergente la valori diferite: termenii impari tind la 1⁄2, iar cei pari la 0), deci 1 − 2 + 3 − 4 + ... nu este sumabilă după metoda (C, 1) a lui Cesàro.
Există două generalizări bine-cunoscute pentru sumarea lui Cesàro: dintre acestea, cea mai simplă din punct de vedere conceptual este șirul (H, n) de metode de sumare, cu n număr natural arbitrar. Suma (H, 1) este sumarea lui Cesàro explicată mai sus, iar metodele succesive din șir se obțin prin aplicarea repetată a metodei de sumare a lui Cesàro pe șirurile de medii aritmetice anterioare. Mai sus, subșirul mediilor pare converge la 1⁄2, în timp ce cel al mediilor impare este constant egal cu 0, de aceea șirul (H, 2) al mediilor aritmetice ale mediilor aritmetice (H, 1) / (C, 1) va converge către media aritmetică dintre 0 și 1⁄2, anume 1⁄4.[4][N 3] Deci seria 1 − 2 + 3 − 4 + ... este sumabilă (H, 2) la 1⁄4.
Notația prin «H» a acestor metode succesive provinde de la Otto Hölder, care a demonstrat pentru prima dată în anul 1882 ceea ce matematicienii acum consideră drept legătura dintre metoda lui Abel și sumările (H, n); iar seria 1 − 2 + 3 − 4 + ... a fost primul său exemplu.[5][6][N 4] Faptul că 1⁄4 este suma (H, 2) a seriei 1 − 2 + 3 − 4 + ... garantează faptul că este și suma conform metodei lui Abel; aceasta va fi dovedită în mod direct mai jos.
Cealaltă generalizare a metodei de sumare a lui Cesàro este șirul de metode (C, n). A fost dovedit ulterior faptul că sumările (C, n) și (H, n) dau întotdeauna aceleași rezultate, dar istoria începuturilor lor diferă. În anul 1887 Cesàro aproape a reușit să definească însumările (C, n), dar s-a limitat la câteva exemple. În special, el a obținut suma de 1⁄4 pentru 1 − 2 + 3 − 4 + ..., printr-o metodă care poate fi acum numită (C, n), dar care nu era justificată la momentul respectiv. El a definit apoi în mod formal metodele (C, n) în 1890, pentru a formula teorema conform căreia produsul Cauchy între o serie sumabilă (C, n) și una sumabilă (C, m) este o serie sumabilă (C, m + n + 1).[7]
Abel

Într-un raport din anul 1749, Leonhard Euler admite că seria diverge, dar planifică să-i găsească suma:
- „...când se spune că suma seriei 1−2+3−4+5−6 etc. este 1⁄4, poate părea paradoxal. Pentru că adunând 100 de termeni ai acestei serii se obține −50, iar suma a 101 termeni este +51, ceea ce diferă destul de mult de 1⁄4, iar această diferență crește odată cu mărirea numerului termenilor. Dar eu am observat mai devreme că este necesar să se atribuie noțiunii de adunare un sens mai larg...”[8][N 5]
Euler a propus generalizări ale noțiunii de „adunare” de mai multe ori. În cazul seriei 1 − 2 + 3 − 4 + ... , ideile lui sunt similare cu ceea ce este acum cunoscut sub numele de metoda de sumare a lui Abel:
- „...nu mai este dubios că suma seriei 1−2+3−4+5 + etc. este de 1⁄4; întrucât provine din dezvoltarea formulei 1⁄(1+1)2, a cărei valoare este incontestabil 1⁄4. Ideea devine mai clară după luarea în considerare a seriei generale 1 − 2x + 3x2 − 4x3 + 5x4 − 6x5 + &c. care apare în urma dezvoltării expresiei 1⁄(1+x)2, cu care această serie este într-adevăr egală după alegerea lui x = 1.”[9]
Există mai multe modalități de a vedea că, cel puțin pentru valorile absolute |x| < 1, Euler are dreptate că
Membrul drept poate fi dezvoltat în serie Taylor, sau se poate folosi algoritmul de împărțire a polinoamelor. Pornind de la membrul stâng, se poate înmulți de două ori cu (1+x) sau se poate ridica la pătrat seria geometrică 1 − x + x2 − ... . Euler sugereză de asemenea diferențierea termen cu termen a seriei din urmă.[N 6]
Din punctul de vedere modern, seria de puteri 1 − 2x + 3x2 − 4x3 + ... nu definește o funcție pentru x = 1, așa că valoarea nu poate fi pur și simplu înlocuită în expresia dezvoltată. Deoarece funcția este definită pentru toți |x| < 1 , se poate lua în continuare limita când x se apropie de 1, aceasta fiind definiția sumării lui Abel:
Euler și Borel
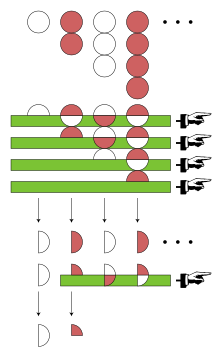
Euler a aplicat o altă tehnică seriei: transformarea lui Euler, una din invențiile sale proprii. Pentru a calcula transformata lui Euler a unei serii alternată, se va folosi șirul de termeni pozitivi care o constituie; în cazul de față, acesta este 1, 2, 3, 4, ... . Primul număr al acestui șir se notează cu a0.
Apoi, trebuie calculate diferențele dintre termenii succesivi ai seriei 1, 2, 3, 4, ... ; acestea sunt 1, 1, 1, 1, ... . Primul termen al acestui șir se notează cu Δa0. Transformarea lui Euler folosește și următoarele diferențe ale diferențelor (prin tot mai multe iterații), dar toate diferențele dintre termenii șirului 1, 1, 1, 1, ... sunt 0, și de asemenea cele ulterioare vor fi tot 0. Transformata Euler a seriei inițiale 1 − 2 + 3 − 4 + ... este calculată în acest caz ca fiind:
Folosind terminologia modernă, se poate spune că seria 1 − 2 + 3 − 4 + ... este sumabilă Euler la 1⁄4.
Sumabilitatea Euler implică și un alt tip de sumabilitate, astfel că reprezentând 1 − 2 + 3 − 4 + ... ca
se obține seria de puteri (convergentă pe tot domeniul):
Suma Borel a seriei 1 − 2 + 3 − 4 + ... este așadar:[10]
Definiția modernă a însumării
În înțeles modern, însumarea este un procedeu care asociază unei serii divergente o altă serie, potențial convergentă (iar apoi, suma acesteia din urmă). Astfel, transformarea (însumarea) lui Euler se poate scrie ca produsul dintre o matrice (infinită) și șirul termenilor unei serii date. În cazul în care rezultatul este o serie convergentă, seria inițială se numește sumabilă Euler. În cazul în care transformarea este aplicată unui serii deja convergente, rezultatul este o serie (mai rapid) convergentă către aceeași sumă.
Generalizări

Produsul Cauchy triplu al seriei 1 − 1 + 1 − 1 + ... (cu ea însăși) este 1 − 3 + 6 − 10 + ... , seria alternată de numere triunghiulare, în cazul căreia sumele (cel puțin conform metodelor de sumare ale lui Abel și Euler) sunt egale cu 1⁄8.[11] Produsul Cauchy cvadruplu al aceleiași serii 1 − 1 + 1 − 1 + ... este 1 − 4 + 10 − 20 + ... , seria alternată de numere tetraedrale, sumabilă Abel la 1⁄16.
O altă generalizare a seriei 1 − 2 + 3 − 4 + ... într-o direcție puțin diferită este seria 1 − 2n + 3n − 4n + ... (seria studiată și cea a lui Grandi se obțin drept cazuri particulare, pentru n = 1 și respectiv 0). Când n este un număr întreg pozitiv, seria are următoarea sumă Abel:[12][N 7]
unde Bn sunt numerele Bernoulli. Pentru n număr par, aceasta se reduce la
Această ultimă sumă a devenit un obiect de batjocură din partea lui Niels Henrik Abel în 1826:
„Seriile divergente sunt în întregime lucrătura diavolului, și este păcat că se încearcă tratarea lor în mod serios. Folosindu-le, poți scoate din ele orice vrei, și din cauza lor s-a generat atât de multă mâhnire și atât de multe paradoxuri. Se poate concepe ceva mai groaznic decât să spui că
- 0 = 1 − 2n + 3n − 4n + etc.
unde n este un număr pozitiv. Iată ceva de tot râsul, prieteni.”[13][N 8]
Profesorul lui Cesàro, Eugène Charles Catalan, descredita de asemenea seriile divergente. Sub influența lui Catalan, Cesàro s-a referit inițial la „formulele convenționale” pentru 1 − 2n + 3n − 4n + ... ca „egalități absurde”, și în 1883, Cesàro și-a exprimat punctul de vedere (tipic epocii) că formulele sunt false, dar că pot fi utile în teorie. Până la urmă, în lucrarea sa din anul 1890, Sur la multiplication des séries, Cesàro a avut o abordare modernă începând de la definiții.[14]
Seriile sunt studiate și pentru valori ne-întregi ale lui n; acestea generează funcția eta Dirichlet. Una din motivațiile lui Euler pentru studierea seriilor similare cu 1 − 2 + 3 − 4 + ... a fost ecuația funcțională a funcției eta, care duce în mod direct la ecuația funcțională a funcției zeta Riemann. Euler câștigase deja faima de a fi determinat valorile acestor funcții pentru numerele naturale pare (în particular rezolvând și problema Basel), și a încercat să găsească valorile pentrul numerele naturale impare (inclusiv constanta lui Apéry); această problemă însă este încă nerezolvată. Cu funcția eta este mai ușor de lucrat folosind metodele lui Euler, deoarece seria Dirichlet a sa este pretutindeni sumabilă Abel; însă seria Dirichlet a funcției zeta este mult mai greu de sumat în cazul divergențelor.[15] De exemplu, perechea seriei 1 − 2 + 3 − 4 + ... în funcția zeta este seria non-alternată 1 + 2 + 3 + 4 + ..., care are aplicații ramificate în fizica modernă, dar care necesită metode de sumare mult mai puternice.
Vezi și
Note explicative
- ^ Negația afirmației "Șirul Sm converge", adică "∃ o valoare x pentru care Sm → x", sau mai precis "∃ x ∈ ℝ ∀ V ∈ 𝒱(x) ∃ N ∈ ℕ ∀ n ∈ ℕ n > N ⇒ Sn ∈ V", este: "∀ x ∈ ℝ ∃ V ∈ 𝒱(x) ∀ N ∈ ℕ ∃ n ∈ ℕ n > N ∧ Sn ∉ V".
- ^ Hardy 1949, p. 6. prezintă un calcul (tot prin liniaritate și stabilitate) care reduce evaluarea seriei la evaluarea seriei lui Grandi, 1 − 1 + 1 − 1 + ….
- ^ Pentru mai multe calcule complete, vezi Weidlich 1950, p. 17-18.
- ^ Ferraro critică explicația lui Tucciarone (Tucciarone 1973, p. 7) asupra modului în care Hölder însuși privea rezultatul general, dar explicațiile celor doi autori în privința tratării seriei 1 − 2 + 3 − 4 + ... sunt similare.
- ^ Deși lucrarea a fost scrisă în 1749, ea nu a fost publicată până în 1768 (Euler et al. 1768).
- ^ De exemplu, Lavine (Lavine 1994, p. 23) pledează pentru algoritmul de împărțire, dar nu îl efectuează; Vretblad (Vretblad 2003, p. 231) calculează produsul Cauchy. Sfatul lui Euler este confuz; vezi Euler et al. 1768, p. 3, 26. . John Baez sugerează chiar o metodă de teoria categoriilor care implică mulțimi etichetate multiplu și oscilatorul armonic cuantic.Baez, John C. Dovada lui Euler că 1 + 2 + 3 + ... =-1/12 (PDF). math.ucr.edu (19 decembrie 2003). Accesată la 11 martie 2007.
- ^ se pare[cercetare originală] că există o eroare în această formulă din Hardy 1949, p. 3.
- ^ Vezi și Markushevich 1967, p. 48. , pentru o traducere diferită de cea originală franceză; tonul rămâne același.
Note
- ^ Hardy 1949, p. 8.
- ^ Beals 2004, p. 23.
- ^ Ferraro 1999, p. 130.
- ^ Hardy 1949, p. 9.
- ^ Ferraro 1999, p. 118.
- ^ Tucciarone 1973, p. 10.
- ^ Ferraro 1999, p. 123-128.
- ^ Euler et al. 1768, p. 2.
- ^ Euler et al. 1768, p. 3, 25.
- ^ Weidlich 1950, p. 59.
- ^ Kline 1983, p. 313.
- ^ Knopp, Konrad (). Theory and Application of Infinite Series. New York: Dover Publications. p. 491. ISBN 0486661652. LCCN 89071388.
- ^ Grattan-Guinness 1970, p. 80.
- ^ Ferraro 1999, p. 120-128.
- ^ Euler et al. 1768, p. 20-25.
Bibliografie
- Beals, Richard (). Analysis: an introduction. Cambridge UP. ISBN 0-521-60047-2.
- Davis, Harry F. (). Fourier Series and Orthogonal Functions. Dover. ISBN 0-486-65973-9.
- Encyclopedic Dictionary of Mathematics, Mathematical Society of Japan, 1954.
- Leonhard Euler, Institutiones Calculi Differentialis, 1755.
- Euler, Leonhard; Willis, Lucas; Osler, Thomas J (). „Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series”. The Euler Archive. Accesat în . Publicat original ca Euler, Leonhard (). „Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques”. Memoires de l'academie des sciences de Berlin. 17: 83–106.
- Ferraro, Giovanni (). „The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics”. Archive for History of Exact Sciences. 54 (2): 101–135. doi:10.1007/s004070050036.
- Grattan-Guinness, Ivor (). The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press. ISBN 0-262-07034-0.
- Hardy, G.H. (). Divergent Series. Clarendon Press. LCCN 91-75377.
- Kline, Morris (). „Euler and Infinite Series”. Mathematics Magazine. 56 (5): 307–314.
- Lavine, Shaughan (). Understanding the Infinite. Harvard UP. ISBN 0674920961.
- Markushevich, A.I. (). Series: fundamental concepts with historical exposition (ed. Traducere în limba engleză a celei de-a treia ediții din 1961 în limba rusă). Hindustan Pub. Corp. LCCN 68-17528.
- Saichev, A.I.; Woyczyński, W.A. (). Distributions in the physical and engineering sciences, Volume 1. Birkhaüser. ISBN 0-8176-3924-1.
- Tucciarone, John (). „The development of the theory of summable divergent series from 1880 to 1925”. Archive for History of Exact Sciences. 10 (1-2): 1–40. doi:10.1007/BF00343405.
- Vretblad, Anders (). Fourier Analysis and Its Applications. Springer. ISBN 0387008365.
- Weidlich, John E. (). Summability methods for divergent series. Stanford M.S. theses. OCLC 38624384.











![{\displaystyle {\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )&+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&+1+(-2+3-4+5+\cdots )&+1+(-2+3-4+5+\cdots )&+1-2+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)+(-2+3&+3-4)+(3-4-4+5)&+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}](https://wikimedia.org/api/rest_v1/media/math/render/svg/511103a5394327bd45eea96fb7dc685dd2986644)



![{\displaystyle {\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d43c146014f7b19d308aac55a97463246ebe5c9)









