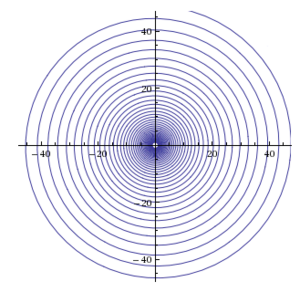
Լոգարիթմական պարույր
Լոգարիթմական պարույր կամ իզոգոնալ պարույր, հատուկ տեսակի պարույր, որը հաճախ հանդիպում է բնության մեջ։
Պատմություն
Լոգարիթմական պարույրն առաջինը նկարագրել է Ալբրեխտ Դյուրերը (1525), որն այն անվանել է «հավերժական (անվերջ) գիծ»[1][2]։ Լոգարիթմական պարույրը նկարագրվել է Դեկարտի կողմից, իսկ ավելի ուշ լայնորեն ուսումնասիրվել է Բեռնուլիի կողմից, ով այն անվանել է Spira mirabilis՝ «զարմանալի պարույր»։ Դեկարտը փնտրում էր մի կոր, որն ունի շրջանագծին նման հատկություն, այնպես որ յուրաքանչյուր կետի շոշափողը յուրաքանչյուր կետում կազմում է նույն անկյունը շառավիղ-վեկտորի հետ։ Նա ցույց է տվել, որ այս պայմանը համարժեք է այն փաստին, որ կորի կետերի բևեռային անկյունները համաչափ են շառավիղ-վեկտորների լոգարիթմներին։
Հավասարումներ
Բևեռային կոորդինատներում կորը կարելի է գրել այսպես.
կամ համապատասխանաբար
որտեղ -ը կետի զրոյից շեղման անկյունն է, r-ը՝ կետի շառավիղ-վեկտորը, a-ն՝ շրջադարձերի շառավիղների համար հաստատուն գործակից, b-ն՝ շրջադարձերի միջև եղած հեռավորության համար հաստատուն գործակիցը, e-ն՝ Էյլերի թիվը։
Պարամետրային ձևով այն կարելի է գրել այսպես.
որտեղ a, b-ն իրական թվեր են, t-ն՝ -ի անալոգը բևեռային կոորդինատներով արտահայտության մեջ։
Հատկություններ
- Լոգարիթմական պարույրի կամայական կետում շոշափողի ձևավորված անկյունը շոշափող կետի շառավղով վեկտորով հաստատուն է և կախված է միայն պարամետր b-ից։ Դիֆերենցիալ երկրաչափության առումով սա կարելի է գրել այսպես.[4]
-
- ֆունկցիայի ածանցյալը համաչափ է b պարամետրին։ Այլ կերպ ասած, դա որոշում է, թե որքան խիտ և ինչ ուղղությամբ է ոլորված պարույրը։ b = 0 սահմանափակման դեպքում, երբ b = 0, պարույրը վերածվում է a շառավղով շրջանագծի։ Հակառակը, երբ b-ն գնում է դեպի անսահմանություն պարույրը ձգտում է ուղիղ գծի։ Լրացուցիչ անկյունը մինչև 90° լրացնող անկյունը կոչվում է պարույրի թեքություն։
- Լոգարիթմական պարույրի պտույտների չափը աստիճանաբար մեծանում է, բայց դրանց ձևը մնում է անփոփոխ։
- Շրջանի երկարության միավորի շառավիղի աճը հաստատուն է։ Հավանաբար, այս հատկության արդյունքում լոգարիթմական պարույրը հայտնվում է որոշակի աճող ձևերով, ինչպիսիք են կակղամորթների կեղևները, արևածաղկի գլուխները, ցիկլոնները և գալակտիկաների պարույրները։
- Եթե անկյունը մեծանում կամ նվազում է թվաբանական պրոգրեսիայով, ապա r-ն մեծանում (նվազում է) երկրաչափական պրոգրեսիայով։
- Պտտելով բևեռային առանցքը բևեռի շուրջ՝ կարելի է հասնել a պարամետրի ամբողջական վերացմանը և հավասարումը բերել ձևի, որտեղ m-ը նոր պարամետր է։
- Պարույրի յուրաքանչյուր կետում կորության շառավիղը համաչափ է պարույրի աղեղի երկարությանը նրա սկզբից մինչև այդ կետը։
Հետաքրքիր փաստեր


- Յակոբ Բեռնուլին ցանկանում էր, որ իր գերեզմանի վրա փորագրվի լոգարիթմական պարույր, բայց փոխարենը սխալմամբ նրա տապանաքարի վրա դրվեց Արքիմեդյան պարույր։ Այնուամենայնիվ, պարույրի շուրջը կտակի համաձայն փորագրված լատիներեն մակագրությունը՝ «EADEM MUTATA RESURGO» («փոխվելով՝ ես նորից հարություն եմ առնում»), ցույց է տալիս, որ նկատի է առնվել հենց լոգարիթմական պարույրը, որն ունի տարբեր փոխակերպումներից հետո իր ձևը վերականգնելու հատկություն։
- Tool-ի երգացանկից «Lateralus» կոմպոզիցիան նվիրված է պարույրներին։
-
a=0.01, b=0.15
-
a=1, b=0.15
-
a=1000, b=0.15
-
Փափկամարմինի կեղևն իր ձևով մոտ է լոգարիթմական պարույրին
-
Ցածր ճնշման տարածք Իսլանդիայի վրա
-
Պարուրաձև գալակտիկայի հորձանուտ
Ընդհանրացում
Լոգարիթմական պարույրը սինուսոիդային պարույր է -ում
Ծանոթագրություններ
- ↑ Albrecht Dürer (1525). Underweysung der Messung, mit dem Zirckel und Richtscheyt, in Linien, Ebenen unnd gantzen corporen.
- ↑ Hammer, Øyvind (2016). «Dürer's dirty secret». The Perfect Shape: Spiral Stories. Springer International Publishing. էջեր 173–175. doi:10.1007/978-3-319-47373-4_41.
- ↑ Priya Hemenway (2005). Divine Proportion: Φ Phi in Art, Nature, and Science. Sterling Publishing Co. ISBN 978-1-4027-3522-6.
- ↑ Boyer, Carl B. (1959). The history of the calculus and its conceptual development : (The concepts of the calculus). [New York]: Dover. ISBN 0-486-60509-4. OCLC 643872.
- ↑ «Logarithmic spiral» (անգլերեն). 2022 թ․ նոյեմբերի 19.
{cite journal}: Cite journal requires|journal=(օգնություն)