Differensiell flategeometri
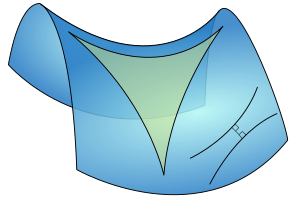
Differensiell flategeometri er den delen av geometrien som omhandler bestemmelse av lengder og areal på krumme flater. Historisk var det vanlig å betrakte en slik generell flate liggende i et euklidsk rom. De geometriske egenskapene til dette rommet gjør det da mulig å finne de tilsvarende egenskapene til flaten. På den måten vil en kurve i flaten kunne betraktes som en romkurve og benyttes til å undersøke flatens krumning.
Fra tidlig astronomi var det kjent hvordan man kunne konstruere en sfærisk geometri på en kuleflate. Rette linjer tilsvarer her storsirkler. Alle slike linjer vil derfor skjære hverandre og dermed ikke oppfylle parallellaksiomet. Denne flaten er symmetrisk og har konstant krumning. Hvordan man i det hele tatt kunne lage en tilsvarende geometri på en vilkårlig flate, var høyst usikkert.
Beskrivelsen av krumme flater ble grundig forbedret rundt 1825 da Carl Friedrich Gauss viste at de intrinsikke egenskapene til flaten kunne bestemmes kun ved målinger i selve flaten slik at de dermed var uavhengig av hvordan flaten plasseres i et ytre rom. Denne innsikten dannet grunnlaget for moderne, differensiell flategeometri. Noen tiår senere kunne Bernhard Riemann utvide betraktningsmåten til Gauss til å gjelde for mangfoldigheter med dimensjon større enn de to som en flate har. Dette åpnet opp for en systematiske utforskning av «krumme rom» som senere skulle bli det matematiske grunnlaget for Einsteins generelle relativitetsteori.
Flater i rommet
Avbilder man en endelig del av det todimensjonale planet E2 på det tredimensjonale, euklidske rommet E3, får man en flate i dette rommet. Hvis den aktuelle delen av planet har de kartesiske koordinatene (u,v), kan denne avbildningen gis ved posisjonsvektoren
for hvert punkt på flaten i E3 når man benytter Einsteins summekonvensjon og summerer over like, latinske indekser fra 1 til 3. Her er ei de kartesiske basisvektorene med det vanlige indreproduktet
uttrykt ved Kronecker-symbolet δij. For hver verdi av de to koordinatene (u,v) vil de tre funksjonene xk(u,v) gi et bestemt punkt på flaten. Det er derfor naturlig å kalle (u,v) for «de intrinsikke koordinatene» til flaten. Holder man v konstant og lar u variere, vil r(u,v) beskrive en kurve i flaten som det er naturlig å kalle en u-koordinatline. Omvendt vil denne vektoren beskrive en v-koordinatlinje når u holdes konstant og v varierer. Gjennom hvert punkt på flaten går det derfor to koordinatlinjer, hver min sin tangentvektor
I hvert slikt punkt danner disse et lokalt plan som er «tangentplanet» til flaten i dette punktet.[1]
Basisvektorer og metrikk
De to koordinatene u og v kan betraktes som krumlinjete koordinater xμ = (u,v) på flaten hvor greske indekser bare tar de to verdiene 1 og 2. En plan kurve i u = u(λ), v = v(λ) i E2 vil nå avbildes på en kurve r(λ) = r(u(λ),v(λ)) på flaten med tangentvektor[2]
hvor nå
kan betraktes som basisvektorer på flaten og dxμ/dλ er de to komponentene til kurvens tangentvektor i denne basisen. Den kvadrerte lengden av denne vektoren er
hvor
er den metriske tensor på flaten. Den definerer et indreprodukt mellom vektorer i samme tangentplan. Lengden av de to basisvektorene kan derfor uttrykkes ved to av de metriske komponentene som
og likedan vinkelen θ12 mellom dem ved den tredje komponenten,
Fra definisjonen følger at den metriske tensoren er symmetrisk slik at gμν = gνμ og den inneholder derfor bare tre uavhengige størrelser. Når g12 = 0 skjærer koordinatlinjene hverandre vinkelrett og metrikken sies å være «diagonal» fordi den tilsvarende matrisen (gμν) er diagonal.
Linjeelement
Lengden til en kurve r(λ) på flaten er gitt ved det kvadrerte, differensielle buelengden
Går kurven gjennom to punkt A og B på flaten, vil lengden av kurven mellom disse to punktene være gitt ved integarlet
hvor . Hvis man i stedet beskrev kurven med parameteren λ' = f (λ) hvor f er en glatt funksjon, ser man at integralet er uforandret. Lengden av kurven har en absolutt verdi, uavhengig av parametriseringen.
Ofte blir notasjonen E = g11, F = g12 og G = g22 benyttet og kalt for «fundamentalstørrelsene av første orden».[1] Linjeelementet tar da formen
etter å ha utført summasjonen over de like indeksene og omtales som «den første, fundamentale formen» til flaten.
Geodetisk kurve
En geodetisk kurve forbinder to punkt slik at avstanden mellom dem målt langs kurven er minst mulig. Den tilsvarer en rett linje i det euklidske rommet. På en flate finnes en slik kurve ved å minimalisere lengdeintegralet L. Det kan gjøres ved variasjonsregning som leder til Euler-Lagrange-ligningen. I dette tilfelle er den
Utregningen her blir spesielt enkel når man velger den naturlige parametriseringen gitt ved kurvens egen buelengde s. Da kan man sette etter å ha utført derivasjonene. Det gir differensialligningen
som kalles den «geodetiske ligningen». Her er
Christoffel-symbolet av andre type hvor gαβ er den inverse matrisen til gαβ. Dette symbolet som ikke er noen tensor, opptrer ofte i forbindelse med bruk av krumlinjete koordinater.
Flateelement
Det differensielle arealet til et lite parallellogram i tangentplanet til flaten definert ved vektorene e1du og e2dv er
Nå er
som er determinanten g = det(gμν) til matrisen for den metriske tensoren. Flateelementet kan da skrives på den enklere formen
Arealet til et endelig stykke av flaten kan herav finnes ved integrasjon.
Vektorproduktet e1 × e2 som opptrer her, er en vektor normal til tangentplanet og derfor også vinkelrett på flaten. Vanligvis defineres den å ha lengde lik med 1 slik at den kan skrives som
Dette er flatens normalvektor som tilfredsstiller N⋅N = 1 sammen med N⋅e1 = N⋅e2 = 0.
Eksempel: Monge-flate
Den enkleste parametrisering av en flate i E3 er gitt ved avbildningen z = f(x,y). Da kalles den ofte for en «Monge-flate» og kan også være en del av en større flate. De to koordinatene i flaten kan da tas å være u = x og v = y slik at posisjonsvektoren til et punkt på den er
Enkel derivasjon gir da de intrinsikke basisvektorene
hvor fu og fv står for den partiellderiverte med hensyn på henholdsvis u og v. De metriske komponentene blir dermed
Som en illustrasjon kan man ta paraboloiden definert ved z = ax2 + by2. Om den skal være elliptisk eller hyperbolsk, avhenger av det relative fortegnet mellom parametrene a og b. Det kvadratiske linjeelementet på denne flaten er dermed
mens arealet er gitt ved dobbelintegralet
Dette er derfor det samme på en elliptisk paraboloide som på en hyperbolsk paraboloide.
Kovariant derivasjon
Et vektorfelt A(x) i det tredimensjonale rommet E3 vil ved avbildningen xk = xk(u,v) gi et vektorfelt A(x) = Aμ(x) eμ på flaten hvor x nå står for koordinatene xμ = (u,v) på flaten. Forandringen av dette feltet langs kurven r(λ) = r(u(λ),v(λ)) i flaten er gitt ved den deriverte[3]
I det første leddet
inngår dxμ/dλ som utgjør komponentene til kurvens tangentvektor v = d r/dλ. Det andre leddet fremkommer fordi basisvektorene på flaten forandrer seg fra sted til sted. Her blir på samme måte
hvor nå
Denne symmetriske størrelsen er i alminnelighet en vektor i det tredimensjonale rommet E3. Den kan derfor splittes opp i en del som ligger i flaten og den gjenværende delen langs normalen N til flaten. Derfor kan man skrive[1]
siden det vil vise seg at i den første delen opptrer Christoffel-symbolet Γαμν på denne måten. Da eμν er symmetrisk, er også dette symbolet og den nye størrelsen bμν symmetrisk i de samme to indeksene. Dens komponenter blir ofte skrevet som b11 = L, b12 = M og b22 = N og kalt for «fundamentalstørrelsene av andre orden».
Av dette følger at den deriverte dA/dλ er en ny vektor med komponenter både parallelt og normalt på flaten. Den delen som ligger i flaten, kalles den kovariant deriverte av vektoren langs tangentvektoren v,
Den kovariant deriverte av A langs basisvektoren eβ er derfor
På samme måte kan kovariante deriverte av tensorer av høyere rang finnes.
Parallellitet
Når den kovariant deriverte av en vektor langs en kurve i flaten er null, sier man at vektoren er parallell med seg selv langs kurven. Det er i analogi med hva man mener med en parallell forflytning av en vektor i det euklidske rommet. Denne definisjonen gjør det mulig å identifisere en klasse av kurver i flaten med den spesielle egenskapen at de har tangentvektorer v = dr/dλ som er parallelle langs en og samme kurve. Ligningen for disse er derfor
Utskrevet på komponentform gir det differensialligningen
som sier at disse spesielle kurvene må være geodetiske. Her kan nå λ være en vilkårlig parametrisering.[3]
Fra definisjonen gμν = eμ⋅eν av den metriske tensoren følger ved derivasjon at
Men nå er
Christoffel-symbolet av første type som derfor oppfyller
Ved å bytte om indeksene og benytte symmetrien mellom dem, kommer man dermed frem til at
Denne beregningen av Christoffel-symbolene gir derfor samme resultat som tidligere.
Ingen av disse konsekvensene av kovariant derivasjon avhenger av at man befinner seg på en todimensjonal flate. De kan derfor tas direkte over til å gjelde på en mangfoldighet med vilkårlig høy dimensjon og beskrevet ved riemannsk geometri. Det er en av fordelene ved å bruke kovariant notasjon og Einsteins summekonvensjon.
Krumning
I utgangspunktet er det ikke klart hvordan man skal definere krumningen til en flate. Men da krumningen til en kurve kan entydig defineres og beregnes, kan man betrakte kurver i flaten. Fra deres krumning får man da også informasjon om flatens krumning.
Det er enklest å betrakte en kurve med naturlig parametrisering r = r(s) i flaten. Den har da en tangentvektor t = d r/ds og krumningsvektor[2]
Her er κ kurvens krumning, mens n er en normert vektor som står vinkelrett på tangentvektoren t. Den har i alminnelighet en komponent normalt på flaten langs normalen N og en annen i flaten langs en vektor e = N×t. Derfor kan man skrive
hvor κg kalles «den geodetiske krumningen» til flaten og κN for «den normale krumningen». De er forbundet ved relasjonen
Da den opprinnelige tangentvektoren kan uttrykkes ved sine komponenter i flaten som
kan krumningsvektoren beregnes med resultatet
Ved her å sette inn for eμν, finner man for den normale krumningen
og for den geodetiske krumingen
Hvis man derfor har benyttet en geodetisk kurve for å undersøke flatens krumning, så blir denne komponenten av krumningen lik med null.[4]
Den avgjørende informasjonen om flatens krumning ligger derfor i normalkrumningen κN og dermed fundamentalstørrelsene av andre orden bμν. Dette kan mer intuitivt forstås utfra et bilde man kan ha av flaten hvor en større krumning vil medføre at normalvektoren N forandrer seg desto raskere. Denne forandringen av normalvektoren kommer til uttrykk i vektoren Nμ = ∂ N/∂xμ. Da N⋅N = 1, må N⋅Nμ = 0. Denne nye vektoren må derfor ligge i tangentplanet slik at man kan skrive
hvor komponentene bνμ foreløbig er ukjente. Men ved å derivere N⋅eμ = 0 på samme måte, finner man
Her kan man gjøre bruk av at N⋅eμν = bμν som til slutt gir at
som er ekvivalent med
Dermed kan disse ukjente koeffisientene også uttrykkes ved fundamentalstørrelsene av andre orden L, M og N samt de metriske komponentene E, F og G som utgjør fundamentalstørrelsene av første orden.
Hovedkrumninger

Normalkrumningen til flaten i et vilkårlig punkt kan skrives som
og avhenger derfor av forholdet du/dv. Dette bestemmer retningen til tangentvektoren. Ved å variere dette, kan man finne to retninger hvor normalkrumningen har et maksimum eller et minimum. Disse to verdiene kalles hovedkrumningene i punktet og tilsvarer to hovedretninger langs flaten.[1]
Hovedkrumningene kan beregnes ved å finne ekstremalverdiene for κN under betingelsen at tangentvektoren t = d r/ds har lengde 1. Denne betingelsen kan inkluderes ved å bruke en Lagrange-multiplikator k som da tilsvarer å finne ekstremalverdiene av uttrykket
hvor tμ = dxμ/ds er komponentene til tangentvektoren. Tar man den deriverte med hensyn på denne komponenten, finner man ligningen
Dette representerer to homogene, lineære ligninger for retningen tμ. De har en løsning bare når determinanten til matrisen i parentesen er null. Skrives den ut, finner man den ny ligningen
hvor igjen g = det(gμν) og b = det(bμν). Røttene κ1 og κ2 til denne andregradsligningen er nå hovedkrumningene. Summen og produktet av dem kan leses direkte ut av ligningen. Dermed finner man for middelkrumningen
mens den gaussiske krumningen er
Fra den samme beregningen følger nå at de to hovedretningene står vinkelrett på hverandre. De fremkommer som skjæringslinjene mellom to plan som står vinkelrett på hverandre og skjærer hverandre langs flatenormalen N. Når middelkrumningen H = 0 i alle punkt, har man med en minimalflate å gjøre. Et eksempel er en katenoide. Er derimot den gaussiske krumningen K = 0 overalt, sies flaten å være flat eller plan.
Da determinanten g > 0, bestemmes fortegnet til den gaussiske krumningen av determinanten b. Når denne er positiv, har begge hovedkrumningene samme fortegn. Et plan like over eller under flaten parallelt med tangentplanet, vil da skjære flaten i en liten ellipse. Et slikt sted på flaten med K > 0, kalles derfor for et elliptisk punkt. Et eksempel er punkt på en ellipsoide. På samme måte vil K < 0 tilsvare et hyperbolsk punkt. Der har de to hovedkrumningene motsatt fortegn, som for eksempel på en sadel. Når K = 0, er en av hovedkrumningene lik med null. Det tilsvarende punktet sies å være parabolsk som for punktene på en sylinder.
Eksempel: Rotasjonsflate
Hvis man i E3 har en plan kurve som kan skrives som z = z(r) hvor r 2 = x 2 + y 2 og denne roteres om z-aksen, da fremkommer en rotasjonsflate hvor hvert punkt er gitt med posisjonsvektoren

Basisvektorer på flaten er derfor
hvor z' = dz/dr. Metrikken er gitt ved linjelementet
slik at
som gir
Normalen til flaten er gitt ved kryssproduktet
som har normen
Dermed har man også den normerte flatenormalen N. Den andre fundamentalformen finnes ved derivasjon av basisvektorene. Det gir
slik at
som gir
Den gaussiske krumningen K = b/g for en slik rotasjonsflate er derfor
Betrakter man som et eksempel paraboloiden z = Ar 2, har den z' = 2Ar og z ' ' = 2A slik at den intrinsikke krumningen blir
Dens dimensjon er den samme som for A2, det vil si en invers, kvadrert lengde som alltid er tilfelle for den gaussiske krumningen.
En kuleflate kan også betraktes som en rotasjonsflate. Øvre halvkule med radius a fremkommer ved å rotere kurven . Da blir
og med motsatt fortegn for nedre halvkule. Det gir krumningen K = 1/a2 som en skulle forvente da begge hovedkrumningene er 1/a. På denne spesielle flaten er krumningen den samme overalt. Det er spesielt og skyldes at flaten har stor symmetri.
Theorema egregium

Hovedkrumningene til flaten er gitt fra variasjonen av normalen N og er uttrykt ved koeffisientene til den andre fundamentalformen. Disse fremkommer ved å betrakte flaten utenfra i det tredimensjonale, euklidske rommet som den befinner seg og er derfor i utgangspunktet eksterne egenskaper til flaten. Men et par år etter at Gauss hadde fremlagt sin differensialgeometri for flater i 1825, kunne han vise at den gaussiske krumningen K er i virkeligheten en intrinsikk egenskap og er gitt ved den første fundamentalformen alene. Den er også uavhengig av hvordan flaten blir parametrisert og kan bestemmes ved kun å foreta målinger i flaten selv, uavhengig av hvordan den er lagt inn i det ytre rommet.
Gauss var så begeistret for denne oppdagelsen at han kalte beviset for «Theorema egregium» - det fantastiske teoremet. Ved å innføre , sier teoremet at den gaussiske krumningen er gitt som[5]
Dette resultatet fant Gauss mens han arbeidet for Georg III av Storbritannia som landmåler i Hannover. Fra sin oppmålinger forsøkte han herav å bestemme Jordens krumning.[6]
En isometrisk avbildning av en flate på en annen bevarer avstanden mellom tilsvarende punkt. Teoremet sier da også at to flater som kan relateres til hverandre på denne måten, har samme gaussiske krumning i korresponderende punkt. Et enkelt eksempel er et plant papirark og en sylinder som begge har null gaussisk krumning. Denne fremkommer ved å rulle sammen arket. Da dette kan gjøres uten å rive opp papiret, er det en isometri. Derimot kan man ikke deformere et papirark til en kuleflate uten å rive opp papiret. Disse to flatene har også forskjellige, gaussiske krumninger.
Ett bevis
Man kan sannsynliggjøre et bevis ved å benytte mer moderne metoder i differensialgeometri basert på differensielle former.[3] Man betrakter da i E3 de tre vektorene ea = (e1, e2, N) hvor disse latinske indeksene går fra 1 til 3. Tar man den dobbelte ytrederiverte av en av disse, gir det
da man er i et euklidsk rom. Her er Ωab konneksjonsformene i denne mobile basisen. Innholdet i parentesen er Riemanns krumningsform Rab i dette rommet og må være identisk null. Tar man komponentene av denne langs flaten hvor indeksene blir greske, har man derfor
På venstre side står nå Riemanns krumningsform Rμν på flaten. Den differensielle 2-formen på høyre side kan uttrykkes ved fundamentalstørrelsene av andre orden via eμν og Nμ. De gir
uttrykt ved basis 1-formene ωμ på flaten. I tillegg er Ω33 = 0 da N har konstant lengde. Komponentene til krumningsformen
er Riemanns krumningstensor som derfor blir
på en flate. Indeksen μ kan her på begge sider senkes ved metrikken gμν. Det gir det ekvivalente resultatet
hvorav man direkte kan avlese symmetriene til denne tensoren. Den er antisymmetrisk i de to første og de to siste indeksene og i tillegg symmetrisk ved ombytte av de to første indeksene med de to siste,
De samme symmetriene opptrer også på mangfoldigheter med høyere dimensjon.[7]
For flaten med sine to dimensjoner, betyr det at Riemann-tensoren har bare en uavhengig komponent. Den kan tas å være
og bestemmer flatens krumning som K = R1212/g. Da Riemann-tensoren alltid kan beregens fra konneksjonsformene som igjen følger fra metrikken, er flatens krumning en intrinsikk egenskap som teoremet sier.
Mobilt aksekors
Beregning av krumningsformen er enklest å utføre i et mobilt aksekors som ved beskrivelse av kurver ved Frenets formler. Man innfører da ortonormerte basisformer slik at metrikken blir diagonal med alle elementer lik med 1. Kalles transformasjonsmatrisen for , har man dermed for de metriske komponentene
Kaller man determinanten til denne matrisen for V, blir dermed determinanten til metrikken g = V 2. Komponentene til Riemann-tensoren vil transformere på tilsvarende vis. Det betyr at
når man hensyn til symmetriene til denne tensoren. I denne ortonormerte basisen blir den gaussiske krumningen dermed
Disse komponentene kan beregnes fra rotasjonsformene som er definert ved «strukturligningen»
De er antisymmetriske i sine to indekser slik at på en flate eksisterer det bare en rotasjonsform . Krumningsformen følger nå generelt fra
hvor siste ledd derfor er null på en flate.
Diagonal metrikk
Som en illustrasjon av denne metoden, kan man betrakte en diagonal metrikk på flaten hvis linjeelement derfor kan skrives på formen
Da skrives den første basisformen som , mens den andre er . Ved ytrederivasjon finner man herav
hvor derivasjon med hensyn på u og v er angitt ved de tilsvarende indeksene. Krumningsformen på denne flaten er derfor
En ny ytrederivasjon gir nå
Komponenten til krumningstensoren kan her avleses direkte slik at den gaussiske krumningen for denne flaten blir
Dette resultatet kan benyttes i mange praktiske sammenhenger. For eksempel, en kuleflate med radius a har merikken
når den beskrives med kulekoordinater. Da er A = a og B = a sinθ slik at Aφ = 0 og Bθ = a cosθ. Krumningen blir dermed
i overensstemmelse med hva man finner med andre metoder.
Konstant krumning
Flater og rom med konstant krumning er maksimalt symmetriske og er viktige i matematikk og fysikk. Deres metriske tensor kan utledes på mange måter. Tar man utgangspunkt i en rotasjonsflate generert ved rotasjon av en kurve om z-aksen, vil hvert punkt på den i polarkoordinater (r,φ,z) være gitt ved
Antar man parametriseringen r = r(λ), z = z(λ) av kurven, finnes metrikken fra linjeelementet
Den blir spesiell enkel når man velger å bruke naturlig parametrisering der λ settes lik kurvens buelengde σ. Da vil r '2 + z '2 = 1 som betyr at r ' ≤ 1. På dette vis har man dermed at
Flaten er nå parametrisert ved de to koordinatene (σ,φ) og har en diagonal metrikk med komponentene A = 1 og B = r(σ). Uttrykket for den gaussiske krumningen forenkles nå til
En flat flate har K = 0 som betyr at r ' er en konstant a ≤ 1. Dermed blir r = aσ + b. Den nye konstanten b kan settes lik null ved et passende valg av parameteren σ. Denne flaten får dermed metrikken
som beskriver overflaten til en rett kjegle. Setter man a = sinα, er α den halve åpningsvinkelen til kjeglen. For den spesielle verdien a = 1 går flaten over til å bli et plan parametrisert ved (σ,φ) som nå er vanlige polarkoordinater i to dimensjoner.
Kuleflate

Funksjonen r(σ) for en flate med konstant, positiv krumning K = 1/a2 hvor a nå er en eller annen lengde, tilfredsstiller differensialligningen
Dette er den harmoniske svingeligningen. Igjen ved å velge nullpunktet for parameteren σ på en passende måte, er løsningen av denne r = c sinσ/a hvor c er en integrasjonskonstant. Det tidligere kravet r ' ≤ 1 betyr nå at c ≤ a.
Den mest symmetriske flaten fremkommer for den spesielle verdien c = a. Innfører man da som ny parameter θ = σ/a, tar metrikken formen
og beskriver dermed den todimensjonale kuleflaten S2 med radius a.
Ved en stereografisk projeksjon kan hvert punkt med koordinater (θ,φ) på kuleflaten avbildes på et plan med polarkoordinater (ρ,φ). Fra figuren ser man sammenhengen
som betyr at
Med denne koordinatiseringen får dermed kuleflaten metrikken
hvor ρ går fra null til uendelig og φ fortsatt varierer mellom 0 og 2π.
En sirkel tilsvarer en kurve ρ = konstant og har en lengde som er forskjellig fra 2π ρ. Koordinaten ρ kan derfor ikke betraktes som en vanlig radius. Men en slik radiell koordinat kan finnes ved å definere
som ikke lenger har noe å gjøre med den opprinnelige r - funksjonen. Metrikken på den krumme kuleflaten tar da formen
Denne nye, radielle koordinaten varierer mellom 0 og a som tilsvarer at den polare vinkelen θ går fra 0 til π /2. For å dekke hele kuleflaten, fortsetter θ å øke fra π /2 til π som betyr at r avtar fra a til null. På denne flaten eksisterer det i så fall sfærisk geometri. Hadde man begrenset seg til den første halvdelen, ville man hatt metrikken for elliptisk geometri som kan benyttes for et projektivt plan. Begge geometriene kan derfor avbildes til innsiden av en sirkel.
Pseudosfære

Metrikken for en flate med konstant, negativ krumning K = - 1/a2 er bestemt av differensialligningen
Hvis man vil at funksjonen r(σ) skal være endelig for alle positive verdier av parameteren σ, vil løsningen av ligningen være r = ce-σ /a . Men ved igjen å velge nullpunktet for σ passende, kan man her sette integrasjonskonstanten c = a. Kurven som genererer denne flaten, er derfor en traktrise i naturlig parametrisering. Den resulterende rotasjonsflaten har dermed metrikken
hvor χ = σ/a. Den ser ut som en uendelig, rett trompet eller lur. Setter man to slike flater sammen med åpningene mot hverandre, får man en ny flate som kalles for «traktoide» eller en pseudosfære da den har motsatt krumning av en sfærisk kuleflate. Dens areal blir
og er derfor det samme som for en vanlig kuleflate med radius a. Den flaten ble funnet i 1868 av Eugenio Beltrami som viste at den kunne brukes til å illustrere ikke-euklidsk geometri.
Hyperbolsk plan
Differensialligningen for en flate med konstant, negativ krumning har også andre løsninger.[3] En viktig klasse tilsvarer løsningen r = c sinhσ/a. Betingelsen r ' ≤ 1 betyr nå at c ≤ a. Er ikke denne oppfylt, kan ikke flaten legges inn i det tredimensjonale, euklidske rommet E3. Men matematisk sett eksisterer løsningen også for c = a. Den beskriver da en flate med metrikken
hvor igjen χ = σ/a og kalles for et hyperbolsk plan som er uendelig stort. Navnet viser tilbake på at denne flaten har hyperbolsk geometri. Hele flaten kan ikke legges inn i det tredimensjonale rommet. Men med en endelig del kan man gjøre det. Slik kan man få frem pseudosfæren på samme måte som en sylinder kan betraktes som en endelig del av det euklidske planet.
Denne krumme flaten kan også koordinatiseres på forskjellige måter. En tilsvarende stereografisk projeksjon som for kuleflaten gir
hvor nå ρ < 2a. Det betyr at
slik at metrikken tar formen
i disse nye koordinatene. På denne måten er også det hyperbolske planet avbildet på innsiden av en sirkel. Alternativt kan man definere
som lar linjeelementet ta formen
Metrikkene til både det euklidske, sfæriske og hyperbolske planet kan skrives på formen
hvor igjen K er den gaussiske krumningen.
Disse flatene med konstante krumninger kan generaliseres til tilsvarende, maksimalt symmetriske rom i tre og fire dimensjoner. De danner grunnlaget for moderne kosmologi basert på Einsteins generelle relativitetsteori.[7]
Referanser
- ^ a b c d R. Tambs Lyche, Matematisk Analyse Bind II, Gyldendal Norsk Forlag, Oslo (1958).
- ^ a b M. R. Spiegel, Vector Analysis, Schaum's Outline Series, New York, (1959).
- ^ a b c d B. O'Neill, Elementary Differential Geometry, Academic Press, New York (1997). ISBN 0-12-526750-9.
- ^ D.J. Struik, Lectures on Classical Differential Geometry, Addison-Wesley, Cambridge, Massachusetts (1950).
- ^ M. Kline, Mathematical Thought from Ancient to Modern Times, Volume 3, Oxford University Press, Oxford (1972). ISBN 978-0-19-506137-6.
- ^ J. Stillwell, Mathematics and Its History, Springer, New York (2010). ISBN 978-1441960528.
- ^ a b C.W. Misner, K.S. Thorne and J.A. Wheeler, Gravitation, W. H. Freeman, San Francisco (1973). ISBN 0-7167-0344-0.
Litteratur
- E. Kreyzig, Differential Geometry, Dover Publications, New York (1991). ISBN 0-486-66721-9.
- T.J. Willmore, An Introduction to Differential Geometry, Clarendon Press, Oxford (1959). ISBN 0-486-48618-4.
Eksterne lenker
- G. Berge, Vektor og tensoranalyse Arkivert 23. mars 2017 hos Wayback Machine., forelesninger ved Universitetet i Bergen (2004).
- N.M. Patrikalakis, Differential Geometry of Surfaces, forelesninger ved MIT (2009).













































































![{\displaystyle K={1 \over 2R}\left[{\partial \over \partial u}\left({F \over ER}{\partial E \over \partial v}-{1 \over R}{\partial G \over \partial u}\right)+{\partial \over \partial v}\left({2 \over R}{\partial F \over \partial u}-{1 \over R}{\partial E \over \partial v}-{F \over ER}{\partial E \over \partial u}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9db7599b8cfa9c0308376a6630452c060d009e5)























![{\displaystyle K=-{1 \over AB}\left[{\partial \over \partial u}\left({1 \over A}{\partial B \over \partial u}\right)+{\partial \over \partial v}\left({1 \over B}{\partial A \over \partial v}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6ce1c35857f7793090df8f8d53542cc41b3c5a2)

![{\displaystyle K=-{1 \over a^{2}\sin \theta }\left[{\partial \over \partial \theta }\left({a\cos \theta \over a}\right)\right]={1 \over a^{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cad6695cc10b1f0dd2342f57cd0e83d6e7d8927)




















