Quadrado
| Quadrado | |
|---|---|
 Quadrilátero regular | |
| Tipo | Polígono regular |
| Arestas e Vértices | 4 |
| Símbolo de Schläfli | {4} |
| Diagrama de Coxeter | |
| Grupo de simetria | Diedral (D4) [4], *44 |
| Área | [1] |
| Ângulo interno (graus) | 90° |
| Propriedades | convexo, cíclico, equilátero, isogonal, isotoxal |

O quadrado é um quadrilátero regular congruente, ou seja, uma figura geométrica com quatro lados de mesmo comprimento e quatro ângulos retos.
Fórmulas métricas
- O perímetro de um quadrado de lado é:
- A área:
- O raio da circunferência inscrita [3]:
- O raio da circunferência circunscrita [4]:
Classificações
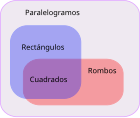
Um quadrado é um caso particular de um: [2]
- quadrilátero plano convexo, pois é um polígono plano convexo de quatro lados;
- paralelogramo, pois os seus lados opostos são paralelos;
- losango, pois os seus lados possuem as mesmas medidas;
- retângulo, pois seus ângulos são todos congruentes;
Propriedades

- As diagonais de um quadrado são vezes maiores que a medida de seus lados. O comprimento das diagonais corresponde ao diâmetro de uma circunferência circunscrita ao quadrado.
- Os lados de um quadrado correspondem à medida do diâmetro de uma circunferência inscrita ao quadrado.
- O quadrado é o quadrilátero de menor perímetro que têm uma dada área. Reciprocamente, o quadrado é o quadrilátero de maior área para um dado perímetro.
- Como o quadrado também é um losango, suas diagonais são perpendiculares, dividem seus ângulos internos na metade e se interceptam no centro do quadrado.
Traçar com régua e compasso
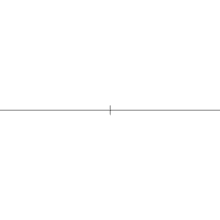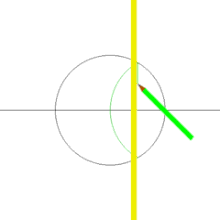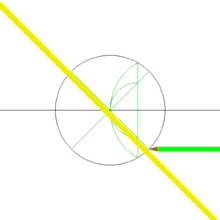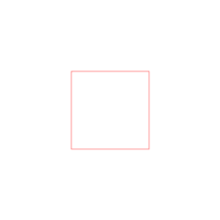
Para traçar um quadrado de diagonais d e centralizado no ponto O:[6]
- Marcar o ponto O onde será o centro do quadrado.
- Desenhe uma linha horizontal que passe pelo ponto O.
- Utilizando como centro o ponto O, trace uma circunferência de diâmetro d, desta forma obteremos dois pontos de intersecção com a reta horizontal do passo 2.
- Sem alterar a abertura do compasso e utilizando agora como centro alguma das duas interesecções do passo 3, trace um arco até cortar em dois pontos a circunferência inicial.
- Una os dois pontos traçados no passo 4 com uma linha reta (vertical), esta reta produzirá um novo ponto de interesecção sobre a reta horizontal inicial.
- Faça o centro com compasso no ponto encontrado no passo 5 e abra o mesmo até o ponto central O e traçe um semicírculo que intercepte em dois pontos na linha vertical do passo 5.
- Desenhe uma linha reta que passe por um dos pontos do passo 6 e pelo ponto central O, estendendo-a até que ambos os lados interseccionem a circunferência inicial do passo 3, isto produzirá sobre a mesma linha dois pontos que são vértices opostas do quadrado e também os extremos de uma das diagonais.
- Repetindo o passo anterior, mas agora com o outro ponto do passo 6 e o ponto central O, obterá os dois pontos que são as vétices opostas do quadrado e também os estremos da segunda diagonal.
- Então, unindo de modo cíclico com linhas retas os quatro pontos de vertice encontrados nos passos anteriores, obterá finalmente o quadrado.
Referências
- ↑ Áreas das figuras planas
- ↑ a b Dolce, O. (2013). Fundamentos de Matemática Elementar 9 ed. [S.l.]: Atual. ISBN 9788535716863
- ↑ Mundo Educação - Circunferência Inscrita no Quadrado
- ↑ MEC - Inscrição e Circunscrição
- ↑ alunosonline.com.br - Calculando a Diagonal do Quadrado e do Retângulo
- ↑ EHow - Como fazer um quadrado em desenho geométrico











