反双曲函数
反双曲函数是双曲函数的反函数。与反圆函数不同之处是它的前缀是ar意即area(面积),而不是arc(弧)。因为双曲角是以双曲线、通过原点直线以及其对x轴的映射三者之间所夹面积定义的,而圆角是以弧长与半径的比值定义。
數學符號
符号 等常用于
等常用于 等。但是这种符号有时在
等。但是这种符号有时在 和
和 之间易造成混淆。
之间易造成混淆。
主值
下表列出基本的反双曲函数。
| 名称
|
常用符号
|
定义
|
定义域
|
值域
|
图像
|
| 反双曲正弦 |
 |
 |
 |
 |

|
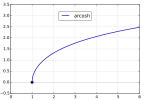
| 反双曲余弦 |
 |
 [註 1] [註 1] |
 |
 |
|
| 反双曲正切 |
 |
 |
 |
 |

|
| 反双曲余切 |
 |
 |
 |
 |

|
| 反双曲正割 |
 |
 |
![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4) |
 |

|
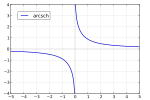
| 反双曲余割 |
 |
 |
 |
 |
|
反双曲函数的导数

求导范例:
设θ = arsinh x,则:

幂级数展开式


















反双曲函数的不定积分

使用分部积分法和上面的简单导数很容易得出它们。
註釋
- ^ 双曲余弦函数是偶函数,所以对于一个y值(y>1),都有两个x值与之对应,取反的时候只取一个(通常是正的)即可。
外部链接
参见


























![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4)






















