Iperbòla (matematicas)

En matematicas, una iperbòla es une corba plana obtenguda coma la dobla interseccion d'un doble còn de revolucion amb un plan. Pòt tanben se definir coma una conica d'excentricitat superiora a 1 o coma l'ensems dels punts que la diferéncia de las distàncias a dos punts fixes es constanta.
Una iperbòla es constituida de dos brancas disjonchas simetricas l'una de l'autra e possedissent doas asimptotas comunas.
Se pòt encontrar l'iperbòla dins fòrça circonstanças coma quand se representa graficament la foncion invèrsa, e aquela de totas las foncions que li son associadas: , o encara dins l'ombra creada per una font de lutz sus una paret, dins la trajectòria d'unes còs dins l'espaci o dins las interferéncias produchas per doas fonts d'ondulacions de meteissa frequéncia. Es tanben la corba seguida, pendent una jornada, pel tèrme de l'ombre del gnomòn de la mòstra de solelh d'estil polar.
L'iperbòla interven dins d'autres objèctes matematics coma los iperboloíds, lo paraboloíd iperbolic, las foncions iperbolicas. Sa quadratura, es a dire lo calcul de l'airal comprés entre una porcion d'iperbòla e son axe principal, es a l'origina de la creation de la foncion logaritme.

Definicions geometricas
Interseccion d'un còn e d'un plan
Se considèra un còn de revolucion engendrada per la rotacion d'una drecha (OA) a l'entorn d'un axe (Ox) e se nomena θ l'angle geometric entre aquelas doas drechas. Se pren d'autre mena un plan que la normala fach amb l'axe (Ox) un angle superieur a π/2-θ. Se lo plan passe pas per O, trenca lo còn seguent una iperbòla. Se lo plan passe per O, trenca lo còn segon doas drechas secantas en O.
Quand una lampa amb paralum es plaçada près d'una paret verticala, la corba que delimita, sus la paret, la zona enlusida e la zona ombrejada es un arc d'iperbòla. De fach, la lutz es difusada segon un còn — los rais luminoses partisson del centre de l'ampola e s'apièjan sulcercle de l'overtura de la lampa — trencat par un plan parallèl a l'axe del còn — la paret.
Es tanben lo meteis principi qu'explica l'existéncia d'iperbòlas sus una mena de mòstra de solelh. Pendent una jornada, los rais solars passant per la punta del gnomòn dessenhan una partida de còn que l'axe, parallèl a l'axe de rotacion de la Tèrra, passa per la punta del gnomòn. L'ombre d'aquela punta, sul plan de la mòstra del solelh dessenha alara una partida d'iperbòla[1], nomenada arc diurn o linha de declinason, intersection del còn e d'un plan. Pendent l'annada, l'angle del còn varia. Als equinòccis, es de 90°, lo còn es un plan e l'ombra dessenha una drecha. Als solsticis, l'angle es de 66° 34' e l'ombra dessenha una iperbòla.
La construccion de l'iperbòla coma seccion d'un còn e d'un plan se pòt relizar amb un compàs perfièch.
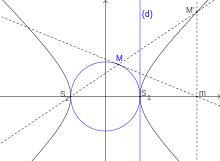
Definicion per fogal e directritz

La distància MF es totjorn egala a un còp e mièg la distància MH
Sián (D) una drecha e F un punt apartenent pas a (D), e siá P lo plan contenent la drecha (D) e lo punt F. Se nomena iperbòla de drecha directritz (D) e de fogal F l'ensems dels punts M del plan P verificant
ont d(M, F) mesura la distància del punt M al punt F e d(M, (D)) mesura la distància del punt M a la drecha (D).
La constanta e es nomenda excentricitat de l'iperbòla. Es caracteristica de la forma de l'iperbòla: se se transfòrma l'iperbòla per una similitud, son excentricitat demora incambiada. Es donc independenta de la causida arbitrària de la marca ortonormada per aquel plan; determina totes los autres rapòrts de distàcias (e totas las diferéncias angularas) mesurats sus l'iperbòla. Mai e es grand, mai l'iperbòla s'envasa, las doas brancas s'apròchant de la directritz. Mai e s'apròcha d'1 mai l'iperbòla se redondís, las doas brancas s'alunhant l'una de l'autra, aquela situada dins lo meteis miègplan que lo fogal s'aprochant d'una parabòla.
Notam K lo projectat ortogonal d'F sus (D). (KF) es alara clarament un axe de simetria de l'iperbòla nomenada axe focal.
L'axe focal trenca l'iperbòla en dos punts nomenats los soms S e S' de l'iperbòla.
La mediatritz del segment [SS'] es, tanben un axe de simetria de l'iperbòla nomenat axe non focal. Lo punt d'interseccion dels dos axes, notat O, es alara lo centre de simetria de l'iperbòla.
Lo cercle de diamètre [SS'] es nomenat cercle principal de l'iperbòla.
La simetria ortogonala al respècte de l'axe non focal envia lo fogal F e la directritz (D) en F' e (D'). Per simetria, l'iperbòla es tanben l'iperbòla de fogal F', de directritz (D') e d'excentricitat e.
Una tala iperbòla possedís en mai doas asimptòtas passant per O e pels punts d'interseccion del cercle principal e de las directriças. Aqueles punts son tanben los projectats ortogonals dels fogals sus las asimptotas[2]. Aquelas doas asimptòtas son perpendicularas, se dich que l'iperbòla es equilatèra.
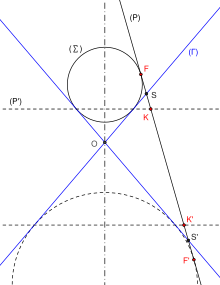
En relacion amb la definition precedenta, l'iperbòla obtenguda coma seccion de còn e de plan pòt èsser definida per fogal e directritz. Se considèra una esfèra (Σ) inscricha dins lo còn (Γ) e tocant lo plan (P) en F (esphèra de Dandelin) e (P') lo plan contenent lo cercle de tangéncia de l'esfèra e del còn. L'iperbòla es de fogal F e de directritz (D) drecha d'interseccion dels dos plans (P) e (P'). Dins lo plan perpendicular a (P) e passant per l'axe del còn, se trapan lo punt F, lo som S e lo punt K. L'excentricitat es donada pel rapòrt SF/SK. Depend pas que de l'inclinason del plan al respècte de l'axe del còn. Se se nomena (d) la traça de (P) dins lo plan perpendicular a (P) passant per l'axe del còn, se se nota α l'angle entre (d) e l'axe del còn e θ l'angle du còn, l'excentricitat es de cos(α)/cos(θ).
Aquela relacion entre fogal, directritz e excentricitat dins una iperbòla es expleitada dins la construccion de las lentilhas divergentas: se l'indici de la lentilha al respècte de la mitat es de e, e se la superfícia concava de la lentilha es una iperbòla de fogal F e d'excentricitat e, lo fais de rais parallèls passant la lentilha, s'espandís coma se los rais venián del fogal F[3]
Definicion bifocala

L'iperbòla es lo luòc geometric dels punts que la diferéncia de las distància als dos fogals es constanta.
Geometricament, aquò fa:
Sián F e F' dos punts distinctes del plan, distants de 2c e siá a un real estrictament comprés entre 0 e c. Se nomena iperbole de fogals F e F' l'ensems dels punts M del plan verificant la proprietat seguenta:
L'axe focal es lo nom de la drecha portant ambedos fogals: es un dels dos axes de simetria de l'iperbòla, lo sol que la trenca. Per aquela rason, se lo nomena atal axe traversièr e sos punts comuns amb la corba son los soms S e S' de l'iperbòla. Lo real de la definition çai dessús aparéis coma la mitat de la distància entre los soms. Las directriças de l'iperbòla passan pel punt del contacte de las tangentas al cercle principal (cercle de diamètre [SS']) eissits dels fogals[4].
En cada punt M d'aquela iperbòla, la bisectritz del sector angular (FMF') se trapan èsser a tangenta en M a la corba.
Aquela construccion de l'iperbòla permet d'explicar la preséncia d'iperbòla pendent d'interferéncias entre doas fonts de meteissa frequéncia. Al punt M lo desfasatge de l'onda al respècte de la font S1 es proporcional a la distància MS1. Lo desfasatge entre l'onda venent de S1 e l'onda venent de S2 es donc proporcional a la diferéncia de las distàncias. Ambedoas ondas s'anullan quand lor desfasatge es egal a (2k+1)π. Ambedoas ondas s'amplifican quand lor desfasatge es de 2kπ. Los punts ont l'onda resultanta a una amplitud nulla e los punts ont l'onda resultanta a una amplitud maximala dessenhant donc un fais d'iperbòlas de fogals S1 e S2.
Existisson de mecanismes amb còrda e carèla expleitant aquela proprietat de las iperbòlas per dessenhar lor traçat. es lo cas del dispositiu realizat per Ibn Sahl al sègle X[5].
Imatge d'un cercle par una omografia
Coma tota conica, l'iperbòla se pòt considerar coma l'imatge d'un cercle per una transformacion projectiva. Mai precisament, se (H) es una iperbòla e (C) un cercle, existís una transformacion projectiva que transforma (C) en (H). Per exemple, l'iperbòla es l'imatge de son cercle principal per una transformacion projectiva que l'expression analitica, dins una marca ortonormada portada pels sieus axes de simetria, es
ont a es lo rai del cercle principal e ± b/a los penjals de las sieunas asimptòtas.
Aquela proprietat permet de transferir a l'iperbòla de las proprietats tocant de las règlas d'incidéncia de drechas dins un cercle, coma lo teorèma de Pascal.
D'entra las transformacions projectivas, n'i a de particularas coma las omologias armonicas. Son d'omologias involutivas de centre I d'axe (d) e de rapòrt -1. Dins aquelas, un punt M, son imatge M', lo centre I e lo punt m d'interseccion de (IM) amb (d) son en division armonica.
Un cercle (C) a per imatge una iperbòla per una omologia armonica de centre I e d'axe (d) se e pas que se l'imatge (d') de l'axe (d) per l'omotecia de centre I e de rapòrt 1/2 trenca lo cercle en dos punts[6]. Reciprocament, una iperbòla essent donada, es possible de trobar de cercles e de las omologias armonicas associadas escambiant iperbòla e cercle. Per exemple:
- Una iperbòla de fogal F, de directritz (d) e d'excentricitat e es l'imatge del cercle de centre F e de rai eh (ont h es la distància entre lo fogal e la directritz) per l'omologia armonica de centre F e d'axe (d1) imatge de (d) dins l'homotecia de centre F e de rapòrt 2[6].
- Una iperbòla equilatèra es l'imatge de son cercle principal per una omologia armonica de centre un dels soms e d'axe (d) passant per l'autre som e perpendicular a l'axe principal de l'iperbòla. Quand l'iperbòla es pas equilatèra, demora l'imatge d'un cercle per una omologia armonica de centre un dels soms, mas lo cercle es pas mai le cercle principal e l'axe passa pas mai per l'autre som. Son d'omologias d'aquel tipe que permeton de montrar le teorèma de Frégier.
Relacions entre las grandors caracteristicas d'una iperbòla

Las grandors (geometricas o numericas) d’una iperbòla son:
- la distància entre lo centre de l'iperbòla e un dels sieus soms mai sovent notada a;
- lo penjal (en valor absoluda) que fan las asimptòtas amb l'axe focal, mai sovent notat b/a;
- la distància separant lo centre de l'iperbòla e un dels fogals, mai sovent notada c;
- la distància separant un fogal F de sa directritz (d) associada, mai sovent notada h;
- la distància separant lo centre de l’iperbòla e una de sas doas directriças, mai sovent notada f;
- l'excentricitat de l’iperbòla (estrictament superiora a 1), mai sovent notada e;
- lo « paramètre » de l’iperbòla, mai sovent notat p, representant lo mièg latus rectum (còrda parallèla a la directritz e passant pel fogal).
De relacions existisson entre aquelas grandors:
- se l'iperbòla es definida per son excentricitat e la distància entre lo fogal F e la directritz (d), alara:
- se l'iperbòla es donada per la distància entre lo centre e un som e lo penjal de las asimptòtas alara:
- quand se conéis la distància entre lo centre e lo som e l’excentricitat :
- Fin finala, dins la definicion bifocala de l'iperbòla ont son conegudas la longor 2a e la distància 2c entre los fogals:
Equacions
Equacion dins una marca normada portada per las asimptòtas
Cas particular de la foncion invèrsa

L'iperbòla que l'expression matematica es mai simple es la representacion grafica de la foncion definida per , vejatz foncion invèrsa.
Aquela iperbòla es equilatèra que sa doas asimptòtas son ortogonalas. Son excentricitat val .
Cas general
Dins la marca , ont O es lo centre de l'iperbòla e e los vectors unitaris directors de las asimptòtas, l'iperbòla a per equacion[3] : .
Reciprocament, se doas drechas de vectors directors e se trencan en O e se una corba, dins la marca , a per equacion xy= Csta o Csta es un real non nul, alara aqula corba es una iperbòla[7].
Equacions dins de marcas ont l'axe focal es l'axe principal
Se le centre de la marca es le centre de l'iperbòla
Dins una marca que los axes son de simetrie per l'iperbòla, l'axe tracersièr per axe de las abscissis, l'equacion cartesiana se met jos la forma
donant alara las representacions parametricas e per caduna de las brancas.
Un autre parametratge possible es:
Son equacion polara es:
Se le centre de la marca es lo fogal de l'iperbòla
Dins la marca ortonormada ont , l'iperbòla a per equacion cartesiana:
Son equacion polara, dins la metaissa marca es:
ont p = eh es lo paramètre de l'iperbòla.
Equacion generala de conica
De biais general, coma tota conica, una iperbòla a una equacion cartesiana de la forma amb Per qu'una tala equacion siá aquela d'una iperbòla, cal[8] que Dins aquel cas, la conica a per centre lo punt C que las coordonadas (x0, y0) verifican lo sistèma[9]: Un cambiament de marca, prenent per centre lo punt C, mena a l'equacion seguenta: que serà l'equacion d'una iperbòla se e pas que se f(x0, y0) es non nul.
L'iperbòla es equilatèra se e pas que se α = - γ
Equacion matriciala
L'equacion precedenta pòt s'escriure jos forma matriciala:
ont
- ; tx es la transpausada de x;
- A es una matritz 2×2, ;
- ; tb es la transpausada de b;
Totjorn amb la meteissa constenchas.
Proprietats
Interior e exterior
L'iperbòla partetja lo plan en 3 zonas o compausantas connèxas. Coma es la seccion d'un còn e d'un plan, se nomena interior de l'iperbòla las partidas de plan situadas a l'interior del còn, so las zonas que contenon los fogals, e exterior de l'iperbòla la darrièra zona, aquela que conten lo centre de l'iperbòla.
Secantas e soms

Siá M un punt de l'iperbòla de soms S e S' e de centre O. Se per un punt N de l'iperbòla, se mena de parallèlas a (SM) e (S'M), encontran l'iperbòla en dos punts P e P' simetrics al respècte de O[10]. En consequéncia, dins un fais de drechas parallèlas (di) encontrant l'iperbòla, los miègs de las còrdas que determinan aquelas drechas sus l'iperbòla, son alinhadas amb leo centre O de l'iperbòla. De mai, se M es lo punt de l'iperbòlas tal que (SM) siá parallèl a (di) alara la drecha dels miègs es parallèl a (S'M)[11]. Una tala drecha passant pel centre de l'iperbòla es nomenada diamètre de l'iperbòla[12].
Secantas e asimptòtas
Se una drecha trenca l'iperbòla en M e M', alara trenca las asimptòtas en P e P' e los segments [MM'] e [PP'] on lo meteis mièg.
Siá (d) una drecha non parallèla a las asimptòtas. Se per un punt M de l'iperbòla, se dessenha una parallèla a (d), encontra las asimptotas en P e P' e lo produch es independent del punt M[13].
Tangentas
Se l'iperbòla a per equacion la tangenta al punt M de coordonadas (x0, y0) a per equacion[14]:
Coma una tangenta es una secanta particulara, la proprietat de las secantas e dels soms ofrisson un mejan de dessenhar una tangenta en un punt M distincte dels soms: la drecha passant per un dels soms S de l'iperbòla e parallèla a (OM) encontra l'iperbòla en N, la tangenta es alara parallèla a (S'N)[15].
Se M es un punt de l'iperbòla distinct dels soms, la tangenta en M es tanben la bissectritz interiora de l'angle FMF' ont F e F' sont los fogals de l'iperbòla e lo produch de las distàncias dels fogals a la tangenta es totjorn egal a b²[16]. Aquela proprietat a unas aplicacions practicas. Dona un mejans simple de construire la tangenta en un punt coma bissectritz interiora de (F'MF). Dins un miralh de forma iperbolica, los rais eissits d'un fogal son rebatuts coma se vinian d'un autre fogal. Bergery preconisa donc, per evitar las pèrdas de calor, de basir lo fond d'un chiminèa segon un cilindre iperbolic[17].
La tangenta en un punt M trenca las asimptòtas en dos punts P e P' simetrics al respècte de M.

Pel punt O o un punt M interior a l'iperbòla, passa pas cap de tangenta, per un punt situat sus l'iperbòla sus una asimptòta (distinct de O), ne passa pas qu'una e per un punt situat a l'exterior de l'iperbòla, non situada sus las asimptòtas, passa totjorn doas tangentas[18]. Per bastir las doas tangentas eissidas de M, sufís de dessenhar lo cercle de centre M passant per un fogal F e lo cercle de centre F' e de rai 2a. Los cercles s'encontran en N e N', las mediatriças de [FN] e [FN'] son las tangentas cercadas[19]. Per trobar lo punt de contacte, sufís de bastir una parallèla a la tangenta trencant l'iperbòla en dos punts, la drecha passant per O e la mitat de la còrdatanben bastida encontra la tangenta en son punt de contacte. O alara, se pren lo simetric d'un dels fogals al respècte de la tangenta, la drecha jonhent aquel simetric a l'autre fogal encontra la tangenta a son punt de contacte[20].
Cercles
Cercle principal: es lo cercle de diamètre [SS']. Fogal e directritz son en relacion pòl/polar al respècte del cercle principal. Lo cercle principal es tanben la podària de l'iperbòla al respècte de l'un dels fogals (se s'exclusís las interseccions del cercle amb las asimptòtas), es a dire lo luòc dels projectats ortoganals d'aquel ce fogals sus las tangentas[16], çò que fa de l'iperbòla, l'antipodària de son cercle principal al respècte d'un dels sieus fogals.
Cercle director: es un cercle passant per fogal e de rai egal a 2a. Segon la definicion bifocala de l'iperbòla, l'iperbòla es lo luòc dels centres dels cercles passant per F e tangents interiorament o exteriorament al cercle director de centre F'. L'ensems de las médiatriças dels segments [FM], onr M parcors lo cercle director de centre F' dona l'ensems de las tangentas a l'iperbòla, lo cercle director es donc l'ortotomic de l'iperbòla al respècte d'un fogal, es a dire l'ensems dels simetrics de F al respècte de las tangentas[16].
Cercle ortoptic: se l’excentricitat es estrictament compresa entre 1 e √2, existís de punts M per ont passan dos tangentas ortogonalas. L'ensems d'aqueles punts M dessenha un cercle de centre O e de rai √a²-b², nomenat cercle ortoptic de l'iperbòla[21].

Cercles osculators: en tot punt M de l'iperbòla, existís un cercle possedant un punt de contacte triple avec l'iperbòla. Es lo cercle osculator a l'iperbòla al punt M. Son centre, nomenat centre de corbadura, es situat sus la normala a la corba (qu'es tanben la bissectritz exteriora de l'angle FMF') a una distància de M egala al rai de corbadura. Se l'iperbòla a per equacion: lo rai del cercle osculator al punt d'abscissi x0 a per valor[22]: Es possible de dessenhar geometricament lo centre del cercle osculator en M. Se (t) e (n) son respectivament la tangenta e la normala a l'iperbòla al punt M, se traça lo simetric M' de M al respècte de l'axe principal e lo simetric (t') de (t) al respècte de (MM'), aquela drecha encontra la drecha (OM') en N. La perpendiculara a (t') en N encontra la normala (n) al centre de corbadura[23].
La desvelopada de l'iperbòla, es dire lo luòc dels centres de corbadura es una corba de Lamé d'equacion[24]:
Longor e airal
Se M(t0) es un punt de l'iperbòla d'equacion parametrada, ont t0 es comprés entre 0 e π/2, la longor de l'arc SM es que l'integracion necessita l'utilizacion de las integralas ellipticas[25].
L'airal d'una partida de plan terminada per un arc d'iperbòl es a l'origina de la creacion de la foncion logaritme e de las foncions iperbolicas. L'airal de la superfícia terminada per l'iperbòla d'equacion yx=1, l'axe de las abscissis e las drechas d'equacion x=u et x=v es egala a |ln(v/u)|.
Istòria

L'iperbòla es estudiada, dins l'encastre de las conicas, pendent lo periòde grèc. Alara Menechme resolguèt un problèma de dobla proporcionala utilisant una iperbòla d'equacion XY= constanta[26]. Mas per Menechme e sos successors, Euclides e Aristèu, aquela corba possèda qu'una compausanta. La nomenan «conica obtusangla» que la definisson coma l'interseccion d'un còn obtusangla (còn engendrat per la rotacion d'un triangle ABC, rectangle en B, a l'entorn de AB e de tal biais que l'angle de som A siá superior a 45 °) amb un plan perpendicular a sa generatritz[27]. Apollonius de Perge sembla èsser lo primièr d'envisatjar las dos compausantas de l'iperbòla[28]. Es tanben el qui li dona lo nom d'«iperbòla» (ajustament per excès) avent remarcat que l'airal du carrat dessenhat sus l'ordonada es superiora a aquela del rectangle dessenhat sus l'abscissi e que la nautor seriá fixa[28].
La recerca de l'airal jos l'iperbòla es entrepresa, en 1647, per Grégoire de Saint-Vincent, que mòstra sa proprietat logaritmica[29]
En 1757-1762, Vincenzo Riccati establís una relacion entre l'airal d'un sector angular dins una iperbòla e las coordonadas d'un punt e definís las foncions cosinus iperbolic e sinus iperbolic per analogia a la relacion existissent dins lo cercle[30].
Bibliografia
- {títol}. ISBN 2-10-049413-9.
- {títol}.
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, ISBN 978-2-916352-08-4
- Méthodes modernes en géométrie de Jean Fresnel
- Bruno Ingrao, Coniques affines, euclidiennes et projectives, C&M, ISBN 978-2-916352-12-1
Annèxas
Articles connèxes
Ligams extèrnes
- (fr) ferréol, Robert; mandonnet, Jacques; esculier, Alain, Hyperbole.
- (fr) hubaut, Xavier, professor emerit de l'Universitat Liura Brussèlas, Les théorèmes belges.
Nòtas e referéncias
- ↑ Du moins cela est vrai pour tous les cadrans horizontaux situés entre les cercles polaires et tous les cadrans verticaux situés au delà des tropiques
- ↑ Tauvel 2005, p. 392
- ↑ 3,0 et 3,1 Robert Ferréol, hyperbole, sur L'Encyclopédie des formes mathématiques remarquables
- ↑ Conséquence de Tauvel 2005, p. 392, prop. 24.1.16
- ↑ Boris A. Rosenfeld et Adolf P. Youshkevitch, « Géométrie », dans Histoire des sciences arabes, t. 2, Seuil, , p. 97
- ↑ 6,0 et 6,1 Extraits de la conférence de Michel Guillerault lors de l’université d'été 93, 3 - Conique comme transformée de cercle par homologie harmonique, sur le site de Cabri-Geomètre.
- ↑ Tauvel 2005, p. 392-393
- ↑ Tauvel 2005, p. 414
- ↑ Tauvel 2005, p. 412
- ↑ Bergery 1843, p. 145 prop.218
- ↑ Bergery 1843, p. 148 prop. 223)
- ↑ Encyclopedia universalis, 1990, vol.6, p.386(b)
- ↑ Tauvel 2005, p. 401
- ↑ Tauvel 2005, p. 396
- ↑ Bergery 1843, p. 163 prop. 249
- ↑ 16,0 16,1 et 16,2 Tauvel 2005, p. 398
- ↑ Bergery 1843, p. 177
- ↑ Tauvel 2005, p. 397.
- ↑ Bergery 1843, p. 171 prob.b
- ↑ Bergery 1843, p. 172 prob. e
- ↑ Tauvel 2005, p. 402
- ↑ d'après Robert Ferréol, Hyperbole, sur L'Encyclopédie des formes mathématiques remarquables
- ↑ d'après Bergery 1843, p. 180
- ↑ Serge Mehl, développée de l'hyperbole sur le site ChronoMath
- ↑ Serge Mehl, Fonction et intégrale elliptique - Arc d'hyperbole, sur le site ChronoMath
- ↑ Vitrac, Ménechme, l'inventeur des sections coniques ?
- ↑ Vitrac, La génération des coniques selon Aristée
- ↑ 28,0 et 28,1 Vitrac, L'approche d'Apollonius Error de citacion : Etiqueta
<ref>no vàlida; el nom «apollonius» està definit diverses vegades amb contingut diferent. - ↑ Jean-Pierre Legoff, « De la méthode dite d'exhaustion : Grégoire de Saint-Vincent (1584 - 1667) », dans La Démonstration mathématique dans l'histoire, IREM de Lyon, , p. 215
- ↑ Robert E. Bradley, Lawrence A. D'Antonio, C. Edward Sandifer, Euler at 300: An Appreciation, MAA, 2007, p. 99