Рух Рейдемейстера

В математичній теорії вузлів рухом (перетворенням) Рейдемейстера називають один з трьох локальних рухів на діаграмі зачеплення. 1927 року Джеймс Александер^[ru] і Бріггс, а також незалежно від них Курт Рейдемейстер, показали, що дві діаграми, які відносяться до одного вузла, з точністю до плоскої ізотопії можуть бути перетворені одна в іншу за допомогою послідовного застосування одного з трьох рухів Рейдемейстера.

Рухи Рейдемейстера

Тип I	Тип II

Тип III

Кожен рух діє на невеликій ділянці діаграми і буває одного з трьох типів:

Тип I. Скручування і розкручування в будь-якому напрямку.

Тип II. Переміщення однієї петлі цілком через іншу.

Тип III. Переміщення нитки цілком під або над перетином.

Зауважимо, що інші частини діаграми не зображені на схемі руху, а також, що плоска ізотопія може спотворити малюнок. Нумерація типів рухів відповідає числу ниток, залучених до нього, приміром, рух типу II діє на двох нитках діаграми.

Один з важливих випадків, коли потрібні рухи Рейдемейстера — це визначення інваріантів вузлів. Інваріант визначають як властивість діаграми вузла, яка не змінюється за будь-яких рухів Рейдемейстера. Багато важливих інваріантів можна визначити таким чином, зокрема поліном Джонса.

Тільки рухи типу I змінюють число закрученості зачеплення. Рух типу III — єдиний, який не змінює число перетинів на діаграмі.

В застосуваннях, таких як числення Кербі^[ru], в якому шуканий клас еквівалентності діаграм вузла є не вузлом, а оснащеним вузлом, необхідно замінити рух типу I рухом «модифікованого типу I» (тип I'), що складається з двох рухів типу I у протилежних напрямках. Рух типу I' не зачіпає ні оснащеності зачеплення, ні повного індексу звивання діаграми вузла.

Модифікований рух Рейдемейстера

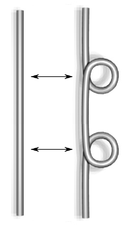
Тип I'

Брюс Трейс показав, що дві діаграми пов'язані тільки рухами типів II і III тоді і тільки тоді, коли в них однакові числа закрученості і обертання. Крім того, спільна робота О. Остлунд, В. О. Мантурова і Т. Хаге показує, що для кожного вузла є така пара діаграм, що будь-яка послідовність рухів Рейдемейстера, яка переводить одну діаграму в іншу, повинна складатися з рухів усіх трьох типів. Олександр Ковард показав, що для діаграм зачеплень, які представляють еквівалентні зачеплення, є послідовність рухів, упорядкована за типами: спочатку виконуються рухи типу I, потім — типу II, типу III і знову типу II. Рухи до рухів типу III збільшують число перетинів, а після них — зменшують.

В іншому руслі, Стефан Галатоло, і незалежно Джоел Хас і Джеффрі Лагар'яс (з кращим обмеженням), показали, що існує верхня межа (яка залежить від числа перетинів) кількості рухів Рейдемейстера, необхідних для перетворення діаграми тривіального вузла на його стандартну діаграму. Це надає малопродуктивний алгоритм для розв'язання задачі розв'язування.

Чюїчіро Хаяші довів, що є також верхня межа, яка залежить від числа перетинів, рухів Рейдемейстера, необхідних для розщеплення зачеплення

Література

J. W. Alexander; G. B. Briggs, On types of knotted curves. Ann. of Math. (2) 28 (1926/27), no. 1-4, 562—586.
Kurt Reidemeister, Elementare Begru"ndung der Knotentheorie, Abh. Math. Sem. Univ. Hamburg 5 (1926), 24-32
Bruce Trace, On the Reidemeister moves of a classical knot. Proc. Amer. Math. Soc. 89 (1983), no. 4, 722—724.
Tobias Hagge, Every Reidemeister move is needed for each knot type. Proc. Amer. Math. Soc. 134 (2006), no. 1, 295—301.
Stefano Galatolo, On a problem in effective knot theory. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 9 (1998), no. 4, 299—306 (1999).
Joel Hass; Jeffrey Lagarias, The number of Reidemeister moves needed for unknotting. J. Amer. Math. Soc. 14 (2001), no. 2, 399—428
Chuichiro Hayashi, The number of Reidemeister moves for splitting a link. Math. Ann. 332 (2005), no. 2, 239—252.