Loi du cosinus surélevé
Loi du cosinus surélevé
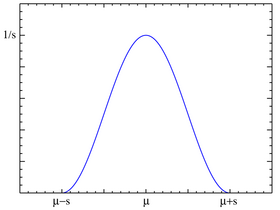
Densité de probabilité
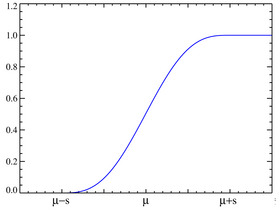
Fonction de répartition
Paramètres
μ
∈
R
{\displaystyle \mu \in \mathbb {R} }
s
>
0
{\displaystyle s>0\,}
Support
x
∈
[
μ
−
s
,
μ
+
s
]
{\displaystyle x\in [\mu -s,\mu +s]\,}
Densité de probabilité
1
2
s
[
1
+
cos
(
x
−
μ
s
π
)
]
{\displaystyle {\frac {1}{2s}\left[1+\cos \left({\frac {x\!-\!\mu }{s}\,\pi \right)\right]\,}
Fonction de répartition
1
2
[
1
+
x
−
μ
s
+
1
π
sin
(
x
−
μ
s
π
)
]
{\displaystyle {\frac {1}{2}\left[1\!+\!{\frac {x\!-\!\mu }{s}\!+\!{\frac {1}{\pi }\sin \left({\frac {x\!-\!\mu }{s}\,\pi \right)\right]}
Espérance
μ
{\displaystyle \mu \,}
Médiane
μ
{\displaystyle \mu \,}
Mode
μ
{\displaystyle \mu \,}
Variance
s
2
(
1
3
−
2
π
2
)
{\displaystyle s^{2}\left({\frac {1}{3}-{\frac {2}{\pi ^{2}\right)\,}
Asymétrie
0
{\displaystyle 0\,}
Kurtosis normalisé
6
(
90
−
π
4
)
5
(
π
2
−
6
)
2
{\displaystyle {\frac {6(90-\pi ^{4})}{5(\pi ^{2}-6)^{2}\,}
Fonction génératrice des moments
π
2
sinh
(
s
t
)
s
t
(
π
2
+
s
2
t
2
)
e
μ
t
{\displaystyle {\frac {\pi ^{2}\sinh(st)}{st(\pi ^{2}+s^{2}t^{2})}\,e^{\mu t}
Fonction caractéristique
π
2
sin
(
s
t
)
s
t
(
π
2
−
s
2
t
2
)
e
i
μ
t
{\displaystyle {\frac {\pi ^{2}\sin(st)}{st(\pi ^{2}-s^{2}t^{2})}\,e^{i\mu t}
modifier
En théorie des probabilités et en statistique , la loi du cosinus surélevé est une loi de probabilité continue définie à partir de la fonction cosinus . Elle dépend de deux paramètres : un réel μ qui est la moyenne et un paramètre positif s décrivant la variance.
Lorsque μ = 0s =1loi du cosinus surélevé standard .
La densité de probabilité de la loi du cosinus surélevé a pour support l'intervalle [μ – s , μ + s ] et est donnée par :
f
(
x
;
μ
,
s
)
=
{
1
2
s
[
1
+
cos
(
x
−
μ
s
π
)
]
pour
μ
−
s
≤
x
≤
μ
+
s
0
sinon.
{\displaystyle f(x;\mu ,s)={\begin{cases}{\frac {1}{2s}\left[1+\cos \left({\frac {x\!-\!\mu }{s}\,\pi \right)\right]\,&{\hbox{ pour }\mu -s\leq x\leq \mu +s\\0&{\textrm {sinon.}\end{cases}
La fonction de répartition de la loi du cosinus surélevé est
F
(
x
;
μ
,
s
)
=
{
0
pour
x
<
μ
−
s
,
1
2
[
1
+
x
−
μ
s
+
1
π
sin
(
x
−
μ
s
π
)
]
pour
μ
−
s
≤
x
≤
μ
+
s
,
1
pour
x
>
μ
+
s
.
{\displaystyle F(x;\mu ,s)={\begin{cases}0&{\hbox{ pour }x<\mu -s,\\{\frac {1}{2}\left[1+{\frac {x-\mu }{s}+{\frac {1}{\pi }\sin \left({\frac {x-\mu }{s}\pi \right)\right]&{\hbox{ pour }\mu -s\leq x\leq \mu +s,\\1&{\hbox{ pour }x>\mu +s.\end{cases}
Moments
Les moments de la loi du cosinus surélevé sont plutôt compliqués, mais sont cependant beaucoup plus simples dans le cas de la loi du cosinus surélevé standard. Cette loi est la loi du cosinus surélevé pour les paramètres μ = 0s =1densité de probabilité de la loi du cosinus surélevé standard est une fonction paire , les moments d'ordre impair sont alors nuls. Les moments d'ordre pair sont donnés par :
E
(
x
2
n
)
=
1
2
∫
−
1
1
[
1
+
cos
(
x
π
)
]
x
2
n
d
x
{\displaystyle E(x^{2n})={\frac {1}{2}\int _{-1}^{1}[1+\cos(x\pi )]x^{2n}\,\mathrm {d} x}
=
1
n
+
1
+
1
1
+
2
n
1
F
2
(
n
+
1
2
;
1
2
,
n
+
3
2
;
−
π
2
4
)
{\displaystyle ={\frac {1}{n\!+\!1}+{\frac {1}{1\!+\!2n}\,_{1}F_{2}\left(n\!+\!{\frac {1}{2};{\frac {1}{2},n\!+\!{\frac {3}{2};{\frac {-\pi ^{2}{4}\right)}
où 1 F 2 fonction hypergéométrique généralisée .
The article is a derivative under the Creative Commons Attribution-ShareAlike License .
A link to the original article can be found here and attribution parties here
By using this site, you agree to the Terms of Use . Gpedia ® is a registered trademark of the Cyberajah Pty Ltd


![{\displaystyle x\in [\mu -s,\mu +s]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/021cb61824dc30c9ce4228710410d45d7b8ea2dd)
![{\displaystyle {\frac {1}{2s}\left[1+\cos \left({\frac {x\!-\!\mu }{s}\,\pi \right)\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9102d632ce3783024691470ecee4a1746288e59a)
![{\displaystyle {\frac {1}{2}\left[1\!+\!{\frac {x\!-\!\mu }{s}\!+\!{\frac {1}{\pi }\sin \left({\frac {x\!-\!\mu }{s}\,\pi \right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de99d5a75fa1d7d33e3f88dafbeec680af501f7c)






![{\displaystyle f(x;\mu ,s)={\begin{cases}{\frac {1}{2s}\left[1+\cos \left({\frac {x\!-\!\mu }{s}\,\pi \right)\right]\,&{\hbox{ pour }\mu -s\leq x\leq \mu +s\\0&{\textrm {sinon.}\end{cases}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c217da3b0b6cd50855cd23569f0f16bb1d540c32)
![{\displaystyle F(x;\mu ,s)={\begin{cases}0&{\hbox{ pour }x<\mu -s,\\{\frac {1}{2}\left[1+{\frac {x-\mu }{s}+{\frac {1}{\pi }\sin \left({\frac {x-\mu }{s}\pi \right)\right]&{\hbox{ pour }\mu -s\leq x\leq \mu +s,\\1&{\hbox{ pour }x>\mu +s.\end{cases}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7496d24accc4c464a55439988bb9b9caa1908fc7)
![{\displaystyle E(x^{2n})={\frac {1}{2}\int _{-1}^{1}[1+\cos(x\pi )]x^{2n}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04729f50cddfc30f1d73ff649bcd285c5ce7aa64)
